Concept of Geospot in Explaining the Source of Geothermal Energy
Received: 24-Jan-2014 / Accepted Date: 26-Jun-2014 / Published Date: 05-Jul-2014 DOI: 10.4172/2090-5009.1000108
Abstract
Source of Geothermal energy which plays an important role in governing the different Geodynamical processes, such as,plate motion, volcanism, hotspot, sialic thickening, convective plumes, mantle plumes, volcanic chain, mid-ocean ridge, island arc, polar wandering, is not properly understood still now. Different tenable sources which have been invoked from time to time do not satisfy the exact requirement. As an alternative, we have hypothesized the formation of a strong magnetic field zone in the core-mantle boundary, which is termed as Geospot. The magnetic loops and arches are formed in the D//region situated near the core- mantle boundary due to the growth or decay of a geospot. When a pair of bipolar regions approaches one another, a current sheet is developed, in which magnetic reconnection takes place. As a result, enormous amount of energy is liberated as a consequence of annihilation of magnetic field of geospot.
Keywords: Geospot; Geothermal energy; Geodynamical processes
17554Introduction
The question as to the source of internal energy inside the earth remains an enigma still today. The following alternatives came up from time to time as the tenable sources of energy which are thought to be responsible for the different kinds of processes occurring inside the earth.
• Radioactive decay is a true source of energy, since its cause is well known. The only long-lived radioactive isotope capable of providing this energy is 40K. From the thermo dynamical and experimental considerations it is clear that most of the potassium at high pressure may follow sulfur and thus be incorporated in the outer core. However, most of the potassium in the Earth appears to reside in the continents and even the upper limit of the amount which may be present in the core does not satisfy the required energy consideration.
• Another source is the latent heat released by crystallization of Fe-Ni on the surface of the inner core. For a cooling rate of 12°C per 109 a, 1012 watts of energy are released. According to this model the material crystallizing on the surface of the inner core contain more nickel than the average outer core, thus producing a nickeldepleted low density layer adjacent to the inner core. This layer is gravitationally unstable and will rise, giving rise to the convection in the outer core.
• The inhomogeneous accretion model explains many geochemical problems and most data support the model in which iron melts in the early earth and gravitationally sinks to the center. The amount of gravitational energy released by such sinking is sufficient to heat the earth by 2000°C, and if retained, to melt the entire earth completely. But the fact that gaseous elements are present in the mantle does not support complete melting and thus most of the early gravitational energy must have been lost.
• Other plausible sources of the thermal energy are the thermal energy released by planetesimal particles during accretion, adiabatic heating originated by compression during accretion, and the possible differentiation of the core, since migration of denser material downward gave rise to friction processes that cause temperature increase.
Among all these sources of heat the radioactivity appears to be the most important thermal source. Although all these primary basic sources of heat could explain the most heat flow at the earth’s surface, but these sources exhibit a linear thermal behaviour. But it is difficult to understand how these sources of thermal energy, necessary for the motion of convective cell, can account for the origin of discontinuous cyclic geological processes. A few cyclic processes, some of which are episodic in nature are enumerated below:
• Plate tectonics is a dynamic phenomenon whose primary cause is not well understood. It is very difficult to realize how radiogenic heat can originate such important Geodynamic process and be of episodic in character.
• Volcanism, hot spots etc are different kinds of thermal manifestations which could not be interpreted properly.
• Expansion–sialic thickening is another phenomenon that includes dynamic, chemical and geophysical phenomena that need explanation.
• Convective plumes is a mechanism of energy motion, whereas, the convection cells need differential thermal gradient to be formed. The causes of these phenomena are not known.
R.E. Sheridan appears to observe the existence of a certain relationship of the dynamic processes, e.g. , plate spreading, global sea– level cycles with the magnetic field variation in a cyclic way. Hence, the cyclic thermal flow appears to be balanced with the magnetics. So far as the energy requirement for the plate movement is concerned, the magnetic energy seems to fulfill the energy criteria of plate-tectonic [1]. The origin of the magnetic field of the earth and the processes causing its reversal are observed in the liquid outer core, whereas the origin of the plate motions and their spreading velocities are controlled by the properties and stresses developed in the lithosphere and asthenosphere. Yet these two phenomena are coupled to each other in some way.
Dynamo Theory
Dynamo theory focuses on the generation of an axisymmetric magnetic field by the action of a mean electromotive force and differential rotation [2]. In mean-field dynamo theory, the field is maintained when the generation effects of the mean e.m.f. and differential rotation balance the decay due to ohmic dissipation. The contributions from the non-linear interaction of the non-axisymmetric components of the problem are parameterized through a prescribed α-effect. So the magnetic induction equation becomes
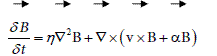 (1)
(1)
where B is the magnetic field, αthe fluid velocity, α the alpha effect and η magnetic diffusivity.
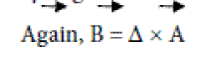 (2)
(2)
In terms of the cylindrical co-ordinates (r,?,z) with the axis of rotation as axis, the components of the mean field can be written as
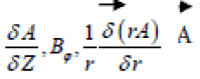
where A is the ? Scomponent of the vector potential of B. Hence, the equation (1) can be written as
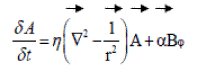 (3)
(3)
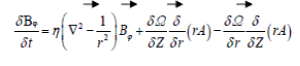 (4)
(4)
where Ω is the local mean angular velocity. In equation (4) the α term is omitted, being negligible compared with the effects of nonuniform rotation. Dynamos based on equations (3) and (4) are known as αΩ dynamos. Those with the Ω term in (4) omitted and α terms reinstated are called α2 dynamos (Cowling, 1976).
Estimate of field strength
The non-dimensional measure of the strength of ohmic diffusion is Λ-1 where Λ is the Elsasser number defined as
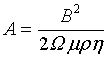 (5)
(5)
Λ=1 corresponds to a field strength of about 20 Gauss=2 × 10-3 Tesla. The poloidal field strength at the core-mantle boundary is only about 5 G. and toroidal field inside the core is 500-1000 G [3].
Emergence Of Magnetic Flux Tube
It has been stated earlier that all the calculations based on Dynamo theory indicate the presence of a large toroidal field of the order 500-1000 G, inside the core; for comparison, the poloidal field at the core boundary is only about 5 G. in explaining the emergence of flux by magnetic buoyancy in the Solar convection zone Parker showed that a horizontal magnetic flux tube, which might be a part of an interior toroidal field, can be lifted to the surface by magnetic buoyancy.
Assuming a horizontally magnetized region near the base of the upper core, the two main mechanisms which may produce loops of field rising to the surface are:
1. An instability started by a perturbation that bends the field lines in a vertical line, like a modified form of the magnetic Raleigh-Taylor instability or the kink instability and
2. An ordered, large–scale convective flow that may pick up magnetic flux in its updraft and lift it to higher layers.
The second alternative has been taken into consideration for explaining the rise of an initially horizontal flux tube through the outer core caused by the development of the kink instability. The flux tube in the initial thermal equilibrium with their surroundings float up to the surface as a whole so rapidly that the instability hardly has time to grow during the journey.
Evolution Of Geospots
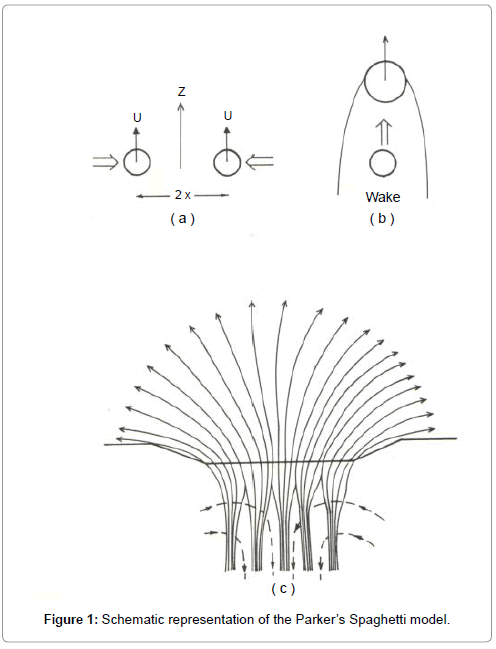
A Geospot may be defined as a region with strong magnetic field assumed to be formed in the core-mantle boundary, probably having the temperature lower than that of the surroundings. In order to explain the evolution of a Geospot, it is presumed that a magnetic flux tube is dragged up by convection to the core-mantle boundary, where its axis is approximately vertical. According to Parker’s spaghetti model [4] a cluster of small flux tube is assembled by hydrodynamic attraction during the formation process. As they rise through upper core convection zone, the flux tubes are attracted to each other due to Bernoulli Effect.
The rising flux tubes (Figure 1a) of radius ‘a’ are moving side-by-side with a constant vertical speed ‘u’ and separation 2x. as the fluid is accelerated between the gap and the cylinders, a force of attraction is produced, it is because, the pressure is reduced there. If the motion be irrotational and if x>>a, then, total kinetic energy of cylinders plus moving fluid can be expressed as:
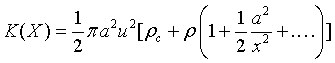
where ρc and ρ are the density of cylinder and fluid, respectively. Force of attraction for a length L
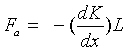
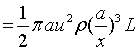
But the magnetic repulsion between the two tubes with field strength B0 is
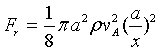
where VA=Alfven speed= 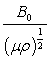
Thus the hydrodynamic attraction is able to overcome the repulsion provided the length of the cylinder exceeds=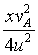
It is also suggested that one flux tube rising behind another (Figure 1b) is attracted in the wake of leading tube. When the flux tubes begin to cluster at the core-mantle boundary, a subsurface downdraft is set up and holds them together by aerodynamic drag. The tubes are kept together in the shape of a circle at the surface because of the effect of the magnetic buoyancy and by a downdraft beneath the Geospot (Figure 1c).
In the core-mantle boundary the iron permeates from the core into the lower most mantles, and mainly oxygen, to some extent Si+Mg enter into the core from the mantle. The iron carries the frozenin magnetic field associated with it and gets it deposited at the upper part of the core-mantle boundary. The sub-surface down draft caused by O-Si-Mg is assumed to flow between the individual flux strands towards the Geospot axis and to provide a confining force by exerting an aero-dynamic drag on the strands. This process also helps to remove some of the excess heat that has piled up below the spot and so reduces the force necessary for confinement.
Biermann was the first to propose that the inhibition of convection through the strong magnetic field [5] will cause the reduced heat flux and temperature in the region where the flux concentration occurs. If the heat be piled up in the magnetized region, the destruction of the spot will occur because pile-up of heat will lead to a pressure-increase in the spot. Thus, the heat excess must be efficiently transported away from the blocking region. The turbulent heat transport outside the magnetic region as proposed by [6] can be efficiently applied for resolving this issue. The diverted heat flux is stored in the core convection zone, where the turbulent heat transport coefficient greatly increases with depth. According to Spruit two time-scales are characteristic for the thermal adjustment of a star after the appearance of a spot.
Diffusive time-scale= 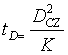
And Kelvin–Helmhotz time of the convection

K=turbulent thermal diffusivity
DCZ=depth, U=thermal contents
Parker (1975) points out the basic relation between the conversion of thermal energy into convective fluid motion and the convective transport of thermal energy. The thermal energy converted into Alfven waves when a strong magnetic field is present. These waves propagate away and dissipate elsewhere, reducing the surface temperature of the spot.
Growth Of Geospots
Let us suppose that a weak magnetic field threads a convection cell. The magnetic energy density=  and the Kinetic energy density =
and the Kinetic energy density = 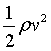
If 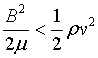
Then, convective motion is unhindered by magnetic field. But if Reynold’s number is very much greater than unity, the magnetic field is carried round and is wound up inexorably by the flow. This process stretches the field lines and increases the magnetic field strength under either of the two reasons
(i) 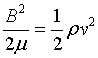 Or, (ii) magnetic Reynolds no≈1.
Or, (ii) magnetic Reynolds no≈1.
The maximum magnetic field strength in a Geospot can be estimated from the theoretical paper on kinematic process of flux expulsion by Weiss [7,8] The relation is given by
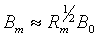
Energy Release Site And Storage
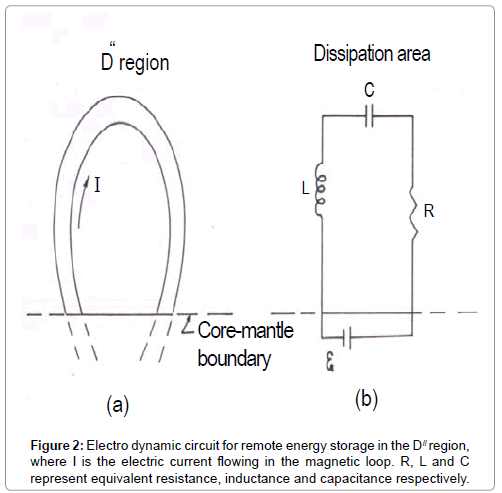
The interface between D// region and the mantle have been presumed to be the site for the liberation of energy which is convected to the mantle. The regions are characterized by a host strong magnetic fields, concentrated in the flux tubes that form loops and arches of different sizes in the D// layer. The foot points of these loops are lying on the upper core-D// region boundary. These loops are formed due to the variation of magnetic flux of the Geospots which are emerging or decaying.
The region where the energy is released, is considered part of a magnetic loop as shown in Figure 2a as D// region is heterogeneous in nature with assemblages of highly conducting as well as insulating alloys, resulting from chemical reaction at the core-mantle boundary and the percolation of iron into the mantle, we are prompted to consider the physical characteristics illustrated in Figure 2b.
An electric current I is assumed to flow in the magnetic loop between the upper core-mantle boundary and the D// region. An illustrating layer between two conducting layers gives rise to the effect of formation of a capacitor C, whereas, R and L give the total resistance and inductance respectively of the equivalent electro dynamic circuit.
Remote Energy Storage
It is assumed that an electric circuit transports energy from the upper core- mantle boundary to the upper most region of D// layer from where the energy in the form of heat is converted to the mantle. This is the heat source necessary for mantle convection.
To examine the global aspect of this sort of storage mechanism, we have used the equation for total current I of the electrical circuit shown in Figure 2b.
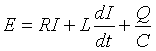
Here E is the e.m.f due to the electro dynamic force generation in the cooler layers of D// region where degree of ionization is low enough so that sufficient neutral atoms are available to carry the positive ions across the magnetic field lines. According to the Dynamo principle
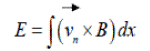
Where 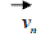
Putting
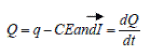
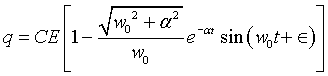
Average Inductive energy over a half cycle
Average capacitive energy over a half cycle
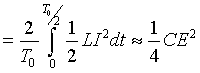
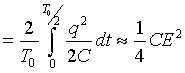
Hence total energy = 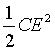
During oscillations the charge may become considerably greater than the final value CE, and consequently the potential difference between the plates may exceed E. This results in a breakdown of the dielectric between the plates, entailing destruction of the capacitor. So at the site where this happens in the D// region, the medium becomes homogeneous.
Formation Of Current Sheet
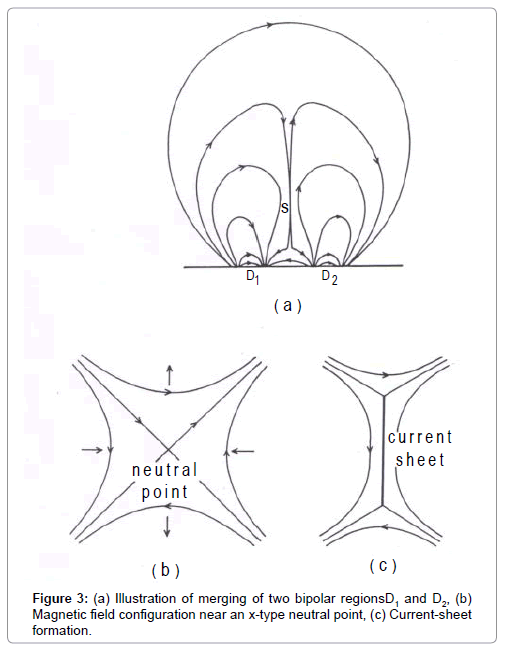
According to Sweet and later developed by Gold-Hoyle a pair of bipolar regions (Figure 3a) approach one another and merge together to form a neutral current sheet. In sketching these field lines it has been considered that the field strength increases with distance from the origin, so that hyperbolae (Figure 3b) are situated successively closer to one another. Any element of the material experiences a resultant magnetic tension due to the outwardly curving field lines. It acts outwards from the origin and is exactly balanced by the magnetic pressure which acts inwards as the magnetic field becomes smaller and smaller if the origin is approached.
Magnetic Reconnection
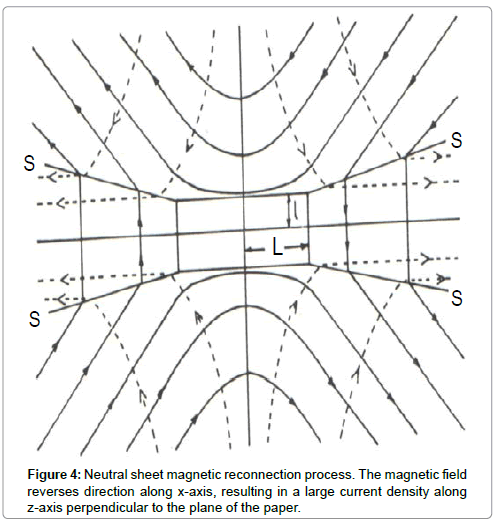
The major problem faced by any mechanism by which the stored magnetic energy is dissipated, is the high conductivity of the material of D// region, with associated long magnetic diffusion times and high magnetic Reynods number, which necessitates the frozen-in field to move the medium and so inhibits its motion. Since the diffusion time scales varies as the square of the characteristics length l associated with changes in magnetic field, it is desirable that this length l should be as small as possible. The neutral sheet (Figure 3c) satisfies this criterion. Such configuration can result in magnetic reconnection. According to Figure 4 the magnetic field component y B reverses direction along the lines X=0. For the sake of simplicity, let us assume that field geometry is independent of the co-ordinate Z (out of the paper).
If a closed rectangle as shown in Figure 4 is taken, then the line integral 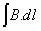 has the value ( By4L) so that applying Stoke’s theorem
has the value ( By4L) so that applying Stoke’s theorem
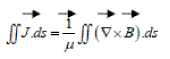
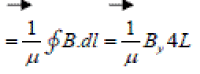
Again , 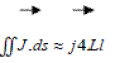
Hence , 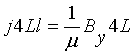
Or, 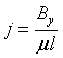
As l becomes smaller, j becomes as large as we please. By omitting the suffix in By we can write B instead, 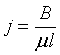
As the width of current sheet l is very small the sheet possesses much larger current densities so that magnetic field may quickly slip through the homogenous conducting medium.
direction along x-axis, resulting in a large current density along z-axis perpendicular to the plane of the paper.
Energy Evolved And Plate Motion
Most current sheets are likely to be rather transient in nature. Let us suppose that the faces of a current sheet have an area of a2. Let the magnetic flux of strength B is carried across the faces into the sheet, where it is converted into heat in a continuous manner. If the field B originally occupies two cubes of side a’ either side of the sheet, it contains magnetic energy of amount
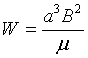
which is released in the form of heat. This energy released is of the order of 1025 Jules which is sufficient for plate motion.
If v be the speed with which magnetic flux is carried into the sheet, then the time of energy release is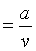
For a steady conversion process, the width of the sheet is
where η is the magnetic diffusivity.
The energy required for the plate motion is of the order of that is evolved during the annihilation of magnetic field by the reconnection mechanism, the energy being carried by the plume eruptions from the D// layer to the asthenosphere with the help of mantle convection. The plate motion as a consequence of the convection process has been discussed in terms of various kinds of models, each treating a specific aspect of the large problem (Richter, 1978). It is observed that the plate velocities do not depend upon the dimension and size of the plates, but they exhibit a bimodal distribution in which subducting plates move relatively fast (~9 cm/year), whereas, the nonsubducting plates move slower (~2 cm/year)
Acknowledgement
The authors are grateful to Professor C.K. Majumder, Ex Director, S.N. Bose National Centre for Basic Sciences, Calcutta for giving various suggestions during the period of this work.
References
- Das TK, Roy D (1997) Proc. Of the Tech. workshop for APT and APSG 1996, Communications Research Laboratory, Kashima, Japan.
- Fearn DR (1993) Solar and Planetary Dynamos, ed. by M. R. E. Proctor, P.C. Mattews and A.M.Rucklidge, Cambridge Univ. Press.
- Chandrasekhar S (1961) Hydrodynamic and Hydromagnetic stability, Oxford U.P
Citation: Das TK, Dhara R (2014) Concept of Geospot in Explaining the Source of Geothermal Energy. Innovative Energy Policies 3: 108. DOI: 10.4172/2090-5009.1000108
Copyright: ©2014 Das TK, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Select your language of interest to view the total content in your interested language
Share This Article
Recommended Journals
Open Access Journals
Article Tools
Article Usage
- Total views: 15552
- [From(publication date): 12-2014 - Sep 01, 2025]
- Breakdown by view type
- HTML page views: 10856
- PDF downloads: 4696