Determinants of Cardiac Ejection Fraction for the Patients with Dobutamine Stress Echocardiography
Received: 10-Nov-2016 / Accepted Date: 12-May-2017 / Published Date: 20-May-2017
Abstract
Objectives: The current article aims to identify the determinants of the baseline cardiac ejection fraction, and also the ejection fraction on dobutamine dose of 558 heart patients who underwent dobutamine stress echocardiography (DSE).
Background: Little is known about the determinants of ejection fraction with DSE.
Methods: The response ejection fraction is positive, heterogeneous, and gamma distributed, so joint generalized linear gamma model fitting is used.
Results: The baseline cardiac ejection fraction (baseEF) increases as the peak heart rate (pkhr) (P=0.0247), or systolic blood pressure (sbp) (P=0.0007), or ejection faction on dobutamine (dobEF) (P<0.001) increases. The baseEF decreases as the double product (DP) of peak heart rate and systolic blood pressure (dp) (P=0.0017), or dobutamine dose given (dose) (P=0.0255) increases. The baseEF increases of the cardiac patients with DSE who have recent angioplasty (newPTCA) (P=0.0101), or history of myocardial infraction (hxofMI) (P=0.0658), or baseline electrocardiogram diagnosis (ecg) at normal level (P=0.0555). The baseEF increases of the cardiac patients with DSE who have not resting wall motion abnormality on echocardiogram (ECDG) (restwma) (P=0.0003), or positive stress echocardiogram (posSE) (P<0.001), or history of angioplasty (hxofPTCA) (P=0.0384). On the other hand, the ejection fraction on dobutamine dose (dobEF) increases as the dp (P=0.0007), or dose (P=0.0110), or baseEF (P<0.001) increases. Also the dobEF decreases as the sbp (P=0.0012) increases. The dobEF increases of the cardiac patients with DSE who have posSE (P<0.001), or new myocardial infraction (newMI) (P=0.0054), or recent bypass surgery (newCABG) (P=0.0049). Again, the dobEF increases of the cardiac patients with DSE who have not newPTCA (P=0.0708). Also the dobEF decreases of the cardiac patients with DSE who have heavy history of smoking (hxofCig) (P=0.0261).
Conclusion: Impacts of pkhr, basal blood pressure, sbp, mbp, dobutamine dose, heart conditions, heavy smoking and others on baseEF and dobEF have been identified based on probabilistic modelling. Most of the present findings and their effects are almost new in the cardiac ejection fraction diagnosis literature.
Keywords: Cardiac ejection fraction; Cardiac parameters;Dobutamine dose; Gamma models; Heart conditions; Non-constant variance
165294Introduction
Ejection fraction (EF) indicates to the percentage of blood that is pumped (or ejected) out of the ventricles with each heartbeat. One of the most important determinants of the severity of systolic heart failure is the ejection fraction (EF). EF acts as a common measure of a person's cardiac function, and it is generally measured by echocadiogram. EF is always low in patients with systolic congestive heart failure. A low EF is always associated with some cardiac diseases. Generally, healthy individuals have EF between 50% and 65% [1]. In practice, normal values depend on the mathematical model (for example EF(%)=100SV/EDV, SV=stroke volume=end-diastolic volume (EDV) -end-systolic volume (ESV)) being used to compute the EF, and it may depend on the person's physical, biochemical, lifestyle, working nature, dietary parameters, etc. [2]. In some articles, the normal values of EF are reported as between 55% and 75% [2,3].
Determinants of the left ventricular ejection fraction (LVEF) and the right ventricular ejection fraction (RVEF) are described for different patients such as suffered from complete left bundle branch block, pulmonary arterial hypertension in many articles [4-17]. For example, some articles [6-8,17] have shown that age, smoking, hyperlipidemia, history of diabetes mellitus are not significant determinants of LVEF. Also, some articles [7,8,10,17] have identified many factors such as systolic blood pressure, New York Heart Association (NYHA) score, sex, history of systolic hypertension, presence of coronary artery disease as the significant determinants of LVEF. Again, for RVEF, it is noted in some articles [12,16] that the gender, age, race/ethnicity, type of pulmonary arterial hypertension (PAH), body mass index, oxygen consumption, systemic blood pressures, right atrial or right ventricular dilation assessed by echocardiography are not significantly associated with the RVEF in bivariate analyses. But in bivariate analyses, higher ventilatory equivalent for carbon dioxide at peak exercise, higher serum, hemoglobin, creatinine, more severe tricuspid regurgitation right atrial pressure (partially), mean pulmonary artery pressure from right heart catheterization (partially), and international normalized ratio (INR) are significantly associated with the lower RVEF [16]. After the adjustment for LVEF, based on multivariate analysis, it is observed that gender, age and higher pulmonary vascular resistance index are significantly associated with the lower RVEF [16].
It is noted that most of the earlier determinants for LVEF and RVEF are determined by using statistical techniques such as simple, multivariate, Logistic regression analyses, Pearson and Spearman rank correlation coefficients, Student-t test, Mann-Whitney U test, Chisquare test, Fisher exact test, F-test, and Normal distribution [7,8,10,16,17]. In earlier studies, the response cardiac EF is assumed as a normally distributed, continuous random variable with constant variance. But in practice, the cardiac ejection fraction is a physiological positive continuous non-normal random variable with non-constant variance. Therefore, the earlier used statistical techniques for determining factors of LVEF and RVEF [7,8,10,16,17] are inappropriate in many cases [18,19]. Thus, the earlier findings invite some doubts and debates. A positive data set (for example, cardiac EF) is generally analyzed either by the log-normal or the gamma model [18-23]. For a positive data set, the variance may be non-constant, as it may have relationship with the mean. The present data set is positive, its variance is non-constant, distribution is non-normal, and the earlier used statistical methods are inappropriate. These issues have motivated us to identify the cardiac EF determinants of the DSE data set [24].
The present report aims to identify the determinants of the baseline cardiac ejection fraction (baseEF), and the ejection fraction on dobutamine dose (dobEF) of the DSE data set [24]. Generally, interested hypotheses of the article are: What are the determinants of the (i) baseEF and (ii) dobEF? The present study has identified many cardiac EF determinants of 558 patients [24] who underwent DSE by separately analyzing the baseEF and dobEF, based on the remaining other explanatory variables (Table 1). These two non-replicated, positive response distributions are non-normal with non-constant variances. So, what are the appropriate statistical modelling techniques for these two responses? Joint generalized linear gamma model [21,25] is the most appropriate statistical technique for the DSE data set [24] which is described in the following section.
| Variable name | Operationalization |
|---|---|
| bhr (y1) | Basal heart rate (bpm) |
| basebp (y2) | Basal blood pressure (mmHg) |
| basedp (x1) | Basal double product (DP) bhr*basebp (bpm*mmHg) |
| pkhr (x2) | Peak heart rate (bpm) |
| sbp (x3) | Systolic blood pressure (mmHg) |
| dp (x4) | DP pkhr¤sbp (bpm*mmHg) |
| dose (x5) | Dobutamine dose (DD) given |
| maxhr (x6) | Maximum heart rate (bpm) |
| pctMphr (x7) | Percent maximum predicted heart rate |
| mbp (x8) | Maximum blood pressure (mmHg) |
| Dpmaxdo (x9) | DP on max DD (bpm¤mmHg) |
| dobdose (x10) | DD at max double product (mg) |
| age (x11) | Age (years) |
| gender (F12) | Gender (male=0, female=1) |
| baseEF (x13) | Baseline cardiac ejection fraction |
| dobEF (x14) | Ejection fraction on dobutamine |
| Chestpain (F15) | Chest pain (yes (y)=0, no (n)=1) |
| restwma (F16) | Resting wall motion abnormality on echocardiogram (ECDG) (y=0, n=1) |
| posSE (F17) | Positive stress ECDG (y=0, n=1) |
| newMI (F18) | New myocardial infraction (MI) (y=0, n=1) |
| newPTCA (F19) | Recent angioplasty (y=0, n=1) |
| newCABG (F20) | Recent bypass surgery (y=0, n=1) |
| death (F21) | Death (y=0, n=1) |
| hxofHT (F22) | History of hypertension (y=0, n=1) |
| hxofDM (F23) | History of diabetes (y=0, n=1) |
| hxofCig (F24) | History of smoking (non-smoker=0, moderate=1, heavy=2) |
| hxofMI (F25) | History of MI (y=0, n=1) |
| hxofPTCA (F26) | History of angioplasty (y=0, n=1) |
| hxofCABG (F27) | History of coronary artery bypass surgery (y=0, n=1) |
| any event (F28) | Death, newMI, newPTCA or newCABG (death=0, no=1) |
| ecg (F29) | Baseline electrocardiogram diagnosis (normal=0, equivocal=1, MI=2) |
Table 1: Operationalization of variables in the analysis.
Materials and Methods
Statistical joint gamma generalized linear models
Some continuous positive heteroscedastic responses have nonnormal error distributions. In practice, they are analyzed by the class of generalized linear models. Generally, the gamma and the log-normal distributions are often used for modelling non-constant variance positive data sets [22], when the response variance has the relationship with its mean. For analyzing the positive response yi's, Nelder and Lee [26] derived a modeling technique (known as the joint generalized linear models (JGLMs)) for the response yi when
E(yi)=μi and Var(yi)=σi tV(μi),
where V(.) is the variance function and σi2, s are the dispersion parameters. The variance function V(.) in GLMs consists of two components. One is V(μI), which depends on the mean changes, and the other is σi2, which is the independent of mean adjustment. The variance function plays the vital role in GLMs as it characterizes the where V(.) is the variance function and σi 2, s are the dispersion parameters. The variance function V(.) in GLMs consists of two components. One is V(μI), which depends on the mean changes, and the other is σi2, which is the independent of mean adjustment. The variance function plays the vital role in GLMs as it characterizes the GLM family distribution. For example, the distribution is Poisson if V(μ)=μ, normal if V(μ)=1, gamma if V(μ)=μ2, etc.
Joint generalized linear models for the mean and dispersion parameters are
ɳi=g(μi)=xit β and εi=h(σi2)=wit γ,
where g(.) and h(.) are respectively, GLM link functions (mean or the variance is a function of the linear predictors) for the mean and the dispersion. Note that xit, and wit are the known row vectors of the study variables for the regression models, and β, γ are unknown regression parameters. These unknown mean parameters are estimated by maximum likelihood (ML) method, while the unknown dispersion parameters are estimated by restricted ML (REML) method [19].
Description of data, JGLM analysis, results and interpretation
Description of data
The considered data set (UCLA stress echocardiography data) in the current study consists of 31 factors/variables on 558 individuals, which is originally taken from a total of 1183 patients referred for DSE between March 1991 and March 1996 to the UCLA Adult Cardiac Imaging and Hemodynamics Laboratories. For every subject, 31 factors/variables (Table 1) have been examined and noted. The considered data set in the current analysis consists of 558 individuals with all non-missing information on 31 factors/ variable. Note that the DSE is widely and successfully applied to identify an individual with or without known coronary artery disease has ischemia [27-29]. The patient population, data collection method, and the DSE used are clearly described in [24]. We have not reproduced the detailed data description in the report as it would increase its length.
Variables
Dependent variables: The present article has aimed to identify the determinants of baseline cardiac ejection fraction and the ejection fraction on dobutamine. Thus, we have considered two separate analyses. The first analysis considers baseline cardiac ejection fraction as the dependent variable, and the remaining others (Table 1) as the independent factors/ variables.
Similarly, the second analysis considers the ejection fraction on dobutamine as the dependent variable, and the remaining others as the independent variables/ factors.
Independent variables: The present data set contains two sets of independent characteristics, which are qualitative and quantitative. Sixteen independent characteristics (Table 1) are qualitative and the remaining others are continuous variables. Table 1 reveals a description of each set of item and how they are operationalized for the current analysis. The percentage of all the levels of the qualitative characters, the means and the standard deviations of all the continuous variables are displayed in Table 2. The average age of the subjects under the study is 67.34 years. The percentage of male (39.43%) patients is lower than the female (60.57%). Note that the average value of baseEF (dobEF) is 55.60 (65.24), while its minimum and maximum values are respectively, 20.00 (23.00) and 83.00 (94.00). Now it is interesting to examine what are the statistical significant determinants of baseline cardiac ejection fraction and the ejection fraction on dobutamine? These issues are addressed in the following sections.
| Variable name | Mean | S.D. | Proportion |
|---|---|---|---|
| Basal heart rate (bpm) | 75.29 | 15.42 | - |
| Basal blood pressure (mmHg) | 135.3 | 20.77 | - |
| Basal double product (DP) bhr*basebp (bpm*mmHg) | 10181 | 2579.75 | - |
| Peak heart rate (bpm) | 120.6 | 22.57 | - |
| Systolic blood pressure (mmHg) | 146.9 | 36.53 | - |
| DP pkhr¤sbp (bpm¤mmHg) | 17634 | 5220.53 | - |
| Dobutamine dose (DD) given | 33.75 | 8.13 | - |
| Maximum heart rate (bpm) | 119.4 | 21.91 | - |
| Percent maximum predicted heart rate | 78.57 | 15.12 | - |
| Maximum blood pressure (mmHg) | 156.0 | 31.71 | - |
| DP on max DD (bpm¤mmHg) | 18550 | 4901.43 | - |
| DD at max double product (mg) | 30.24 | 9.54 | - |
| Age (years) | 67.34 | 12.05 | - |
| Gender (male=0, female=1) | - | - | 0%=39.43,1%=60.57 |
| Baseline cardiac ejection fraction | 55.60 | 10.32 | - |
| Ejection fraction on dobutamine | 65.24 | 11.76 | - |
| Chest pain (yes (y)=0, no (n)=1) | - | - | 0%=69.18, 1%=30.82 |
| Resting wall motion abnormality on echocardiogram (ECDG) (y=0,n=1) | - | - | 0%=53.94, 1%=46.06 |
| Positive stress ECDG (y=0, n=1) | - | - | 0%=75.63, 1%=24.37 |
| Nw myocardial infraction (MI) (y=0, n=1) | - | - | 0%=94.98, 1%=5.02 |
| Recent angioplasty (y=0, n=1) | - | - | 0%=95.16, 1%=4.84 |
| Recent bypass surgery (y=0, n=1) | - | - | 0%=94.09, 1%=5.91 |
| Dath (y=0, n=1) | - | - | 0%=95.70, 1%=4.30 |
| History of hypertension (y=0, n=1) | - | - | 0%=29.57, 1%=70.43 |
| History of diabetes (y=0, n=1) | - | - | 0%=63.08, 1%=36.92 |
| History of smoking (non-smoker=0, moderate=1, heavy=2) | - | - | 0%=53.41, 1%=24.73, 2%=21.86 |
| History of MI (y=0, n=1) | - | - | 0%=72.40, 1%=27.60 |
| History of angioplasty (y=0, n=1) | - | - | 0%=92.65, 1%=7.35 |
| History of coronary artery bypass surgery (y=0, n=1) | - | - | 0%=84.23, 1%=15.77 |
| Death, newMI, newPTCA or newCABG (death=0, no=1) | - | - | 0%=84.05, 1%=15.95 |
| Baseline electrocardiogram diagnosis (normal=0, equivocal=1, MI=2) | - | - | 0%=55.91, 1%=31.54, 2%=12.72 |
Table 2: Summarized statistics.
Baseline cardiac ejection fraction (baseEF) analysis
The current report aims to identify the determinants of the baseline cardiac ejection fraction (baseEF) and the ejection fraction on dobutamine (dobEF). We have examined the baseEF and the dobEF using both the log-normal and the gamma models, which are generally used for modelling a positive data set [18,22,30,31].
These two dependent variables have been identified herein as nonconstant response variance. Moreover, the gamma model analysis gives more better results than the log-normal model for each EF.
Therefore, for each case, only the gamma model analysis results are displayed. The present section displays the gamma fit analysis of baseline cardiac ejection fraction.
For qualitative characters (or factors), we accept the constraint that the effects of the first levels are zero. So, it is considered that the first level of each factor as the reference level by estimating it’s as zero.
Let us assume that ai for i=1,2,3 represents the main effect of B. Thus, â1=0 is accepted, hence, â2=â2 - â1. For example, the difference between the effect of the second and the first levels in the main effect B (i.e., â2 - â1.) represents the estimate of the effect B2.
The continuous response baseline cardiac ejection fraction (with non-constant variance) has been modeled based on the remaining other explanatory variables, using the joint gamma models (Methods section), and the results are displayed in Table 3.
The selected models have the smallest Akaike information criterion (AIC) value in each class. It is well known that AIC selects a model which minimizes the predicted additive errors and squared error loss. Based on AIC (=3232.214), the final gamma fitted models (Table 3) have been selected.
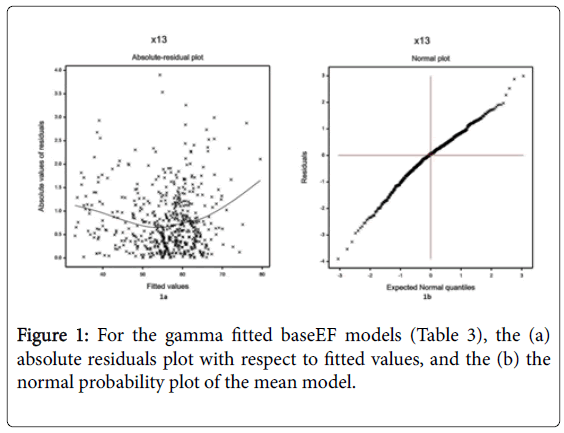
Some partially insignificant effects (basebp, hxoCig, hxofHT), known as confounder in epidemiology, are included in the model. Note that it is not necessary that all the selected effects in the models are significant [30]. The joint GLM diagnostic plots have been examined in Figure 1, for the fitted gamma models in Table 3.
| Model | Covariate | Estimate | Standard error | t-value | P-value |
|---|---|---|---|---|---|
| Mean Model | Constant | 3.0632 | 0.0812 | 37.75 | <0.001 |
| basebp (y2) | -0.0002 | 0.0002 | -1.30 | 0.1934 | |
| pkhr (x2) | 0.0013 | 0.0006 | 2.25 | 0.0247 | |
| sbp (x3) | 0.0015 | 0.0004 | 3.40 | 0.0007 | |
| dp (x4) | -0.0001 | 0.0001 | 3.15 | 0.0017 | |
| dose (x5) | -0.0009 | 0.0004 | -2.24 | 0.0255 | |
| dobEF (x14) | 0.0124 | 0.0004 | 31.37 | <0.001 | |
| restwma (F161) | 0.0269 | 0.0074 | 3.66 | 0.0003 | |
| posSE(F171) | 0.0400 | 0.0087 | 4.60 | <0.001 | |
| newPTCA(F191) | -0.0447 | 0.0173 | -2.58 | 0.0101 | |
| hxofCig (F241) | -0.0032 | 0.0077 | -0.41 | 0.6820 | |
| hxofCig(F242) | 0.0115 | 0.0079 | 1.45 | 0.1476 | |
| hxofMI(F251) | -0.0155 | 0.0084 | -1.84 | 0.0658 | |
| hxofPTCA(F261) | 0.0294 | 0.0142 | 2.08 | 0.0384 | |
| ecg (F291) | -0.0135 | 0.0071 | -1.92 | 0.0555 | |
| ecg (F292) | 0.0069 | 0.0105 | 0.66 | 0.5089 | |
| Dispersion Model |
Constant | -0.1692 | 0.5321 | -0.32 | 0.7506 |
| basebp (y2) | -0.0067 | 0.0041 | -1.63 | 0.1030 | |
| basedp(x1) | 0.0001 | 0.0001 | 2.36 | 0.0185 | |
| mbp(x8) | -0.0060 | 0.0024 | -2.47 | 0.0139 | |
| dobEF(x14) | -0.0605 | 0.0050 | -12.04 | <0.001 | |
| hxofHT(F221) | 0.1879 | 0.1430 | 1.31 | 0.1894 | |
| hxofCABG(F271) | 0.3597 | 0.1725 | 2.09 | 0.0375 |
Table 3: Results for mean and dispersion models of baseline cardiac ejection fraction from gamma fit.
The absolute residual values of the fitted gamma models (Table 3) are plotted with respect to fitted values in Figure 1a. Note that the Figure 1a is almost flat with the running means, indicating that the variance is constant for the fitted model. Figure 1b displays the normal probability plot of the gamma fitted mean model (Table 3), which does not show any lack of fit with respect to variables and outliers, as there is not any gap in the figure.
Results
Interpretations of baseEF analysis
Gamma fitted results of baseEF are displayed in Table 3. The following results and the interpretations can be drawn from Table 3.
(i) The mean baseEF is positively associated with the peak heart rate (pkhr) (P=0.0247). This indicates that the baseEF increases as the pkhr increases, and vice-versa.
(ii) The mean baseEF is positively associated with the systolic blood pressure (sbp) (P=0.0007), indicating that the baseEF increases as the sbp increases.
(iii) The mean baseEF is positively associated with the ejection fraction on dobutamine (dobEF) (P<0.001), indicating that the baseEF increases as the dobEF increases.
(iv) The mean baseEF is positively associated with the resting wall motion abnormality on echocardiogram (restwma) (P=0.0003). The presence and absence of restwma are indicated by the level 0 and 1 (Table 1), respectively. As the association between baseEF and restwma is positive, so baseEF is higher of the cardiac patients with DSE who have no restwma. Note that the factor levels (Table 1) are arranged in the reverse order than the normal presentation, yet the present analyses identify the correct interpretations.
(v) The mean baseEF is positively associated with the positive stress on echocardiogram (posSE) (P<0.001). Levels of posSE are 0 (presence) and 1 (absence) (Table 1). This result indicates that the baseEF is higher of the cardiac patients with DSE who have no posSE. This result focuses the real situation.
(vi) The mean baseEF is positively associated with the history of angioplasty (yes=0, no=1) hxofPTCA (P=0.0384), indicating that the baseEF is higher of the cardiac patients with DSE who have no hxofPTCA, which is observed in practice.
(vii) The mean baseEF is negatively associated with the double product of pkhr and sbp (P=0.0017), indicating that the baseEF decreases as the double product of pkhr and sbp increases.
(viii) The mean baseEF is negatively associated with the dobutamine dose given (dose) (P=0.0255), indicating that the baseEF decreases as the dose increases.
(ix) The mean baseEF is negatively associated with the recent angioplasty (yes=0, no=1) (newPTCA) (P=0.0101), indicating that the baseEF is higher of the cardiac patients with DSE who have newPTCA.
(x) The mean baseEF is negatively associated with the history of myocardial infraction (yes=0, no=1) hxofMI (P=0.0658), indicating that the baseEF is higher of the cardiac patients with DSE who have hxofMI.
(xi) The mean baseEF is negatively associated with the baseline electrocardiogram diagnosis (normal=0, equivocal=1, MI=2) (ecg) (P=0.0555), indicating that the baseEF is higher of the cardiac patients with DSE who have normal ecg.
(xii) The variance of baseEF is positively associated with the double product of basal blood pressure and heart rate (basedp) (P=0.0185), indicating that the baseEF variance increases as the basedp increases.
(xiii) The baseEF variance is positively associated with the history of coronary artery bypass surgery (yes=0, no=1) (hxofCABG) (P=0.0375), indicating that the baseEF variance is higher of the cardiac patients with DSE who have no hxofCABG. That is the baseEF variance is highly scattered of the cardiac patients with no hxofCABG.
(xiv) The baseEF variance is negatively associated with the basal blood pressure (basebp) (P=0.1030), indicating that the baseEF variance increases as the basebp decreases. Similar association is observed between the baseEF variance and the maximum blood pressure (mbp) (P=0.0139).
(xv) The baseEF variance is negatively associated with the dobEF (P<0.001), indicating that the baseEF variance increases as the dobEF decreases. Note that the dobEF has dual reverse effect with the mean and variance of baseEF.
Ejection fraction on dobutamine (dobEF) analysis
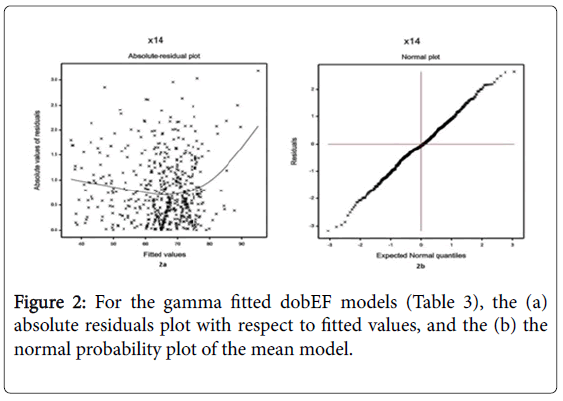
The continuous non-constant variance response ejection fraction on dobutamine has been modeled based on the remaining other explanatory variables, using the joint gamma models, and the results are displayed in Table 4. The selected models have the smallest Akaike information criterion (AIC) value in each class. Based on AIC (=3343.535), the final gamma fitted models (Table 4) have been selected. Note that some insignificant effects are included in both the mean and variance models for proper fitting [30]. The joint GLM diagnostic plots have been examined in Figure 2, for the fitted gamma models (Table 4).
The gamma fitted (Table 4) absolute residual values are plotted with respect to fitted values in Figure 2a. Figure 2a is almost flat except the right tail, with the running means, indicating that the variance is constant for the fitted model. Right tail is increasing due to the largest absolute residual value which is located at the right boundary. Figure 2b displays the normal probability plot of the gamma fitted mean model (Table 4), which does not show any lack of fit. Thus, the fitted models (Table 4) are very close to the unknown true models.
| Model | Covariate | Estimate | Standard error | t-value | P-value |
|---|---|---|---|---|---|
| Mean Model | Constant | 3.3289 | 0.0327 | 101.90 | <0.001 |
| sbp (x3) | -0.0004 | 0.0001 | -3.24 | 0.0012 | |
| dp (x4) | 0.0001 | 0.0001 | 3.40 | 0.0007 | |
| dose (x5) | 0.0010 | 0.0004 | 2.55 | 0.0110 | |
| baseEF (x13) | 0.0149 | 0.0004 | 35.89 | <0.001 | |
| posSE(F171) | -0.0349 | 0.0082 | -4.25 | <0.001 | |
| newMI(F181) | -0.0477 | 0.0171 | -2.79 | 0.0054 | |
| newPTCA(F191) | 0.0314 | 0.0173 | 1.81 | 0.0708 | |
| newCABG(F201) | -0.0495 | 0.0175 | -2.82 | 0.0049 | |
| hxofCig (F241) | -0.0061 | 0.0072 | -0.84 | 0.4012 | |
| hxofCig(F242) | -0.0161 | 0.0072 | -2.23 | 0.0261 | |
| Dispersion Model |
Constant | -1.0093 | 0.4515 | -2.24 | 0.0257 |
| dobdose (x10) | -0.0217 | 0.0068 | -3.19 | 0.0015 | |
| baseEF (x13) | -0.0656 | 0.0063 | -10.35 | <0.001 | |
| posSE(F171) | 0.3381 | 0.1539 | 2.20 | 0.0285 | |
| hxofPTCA (F261) | -0.3560 | 0.2482 | -1.43 | 0.1521 | |
| hxofCABG (F271) | 0.2589 | 0.1748 | 1.48 | 0.1392 | |
| ecg (F291) | 0.2062 | 0.1384 | 1.49 | 0.1368 | |
| ecg (F292) | 0.0516 | 0.2046 | 0.25 | 0.8011 |
Table 4: Results for mean and dispersion models of ejection fraction on dobutamine dose from gamma fit.
Interpretations of dobEF analysis
Table 4 displays the summarized results of dobEF analysis, based on joint gamma models fitting. The following results and interpretations can be drawn from Table 4.
(i) The mean dobEF is positively associated with the dp (P=0.0007), indicating that the dobEF increases as the dp increases. Note that the baseEF and dobEF are oppositely associated with the dp.
(ii) The mean dobEF is positively associated with the dobutamine dose (P=0.0110), indicating that the dobEF increases as the dose increases. Here also the baseEF and dobEF are oppositely associated with the dose.
(iii) The mean dobEF is positively associated with the baseEF (P<0.001), indicating that the dobEF increases as the baseEF increases. Note that the baseEF is also similarly associated with the dobEF.
(iv)The mean dobEF is positively associated with the newPTCA (yes=0, no=1) (P=0.0708), indicating that the dobEF is higher of the cardiac patients with DSE who have no newPTCA. Here also the baseEF and dobEF are oppositely associated with the newPTCA.
(v) The mean dobEF is negatively associated with the sbp (P=0.0012), indicating that the dobEF increases as the sbp decreases. Here also the baseEF and dobEF are oppositely associated with the sbp.
(vi)The mean dobEF is negatively associated with the posSE (yes=0, no=1) (P<0.001), indicating that the dobEF is higher of the cardiac patients with DSE who have posSE. Here also the baseEF and dobEF are oppositely associated with the posSE.
(vii) The mean dobEF is negatively associated with the new myocardial infraction (MI) (yes=0, no=1) (newMI) (P=0.0054), indicating that the dobEF is higher of the cardiac patients with DSE who have newMI.
(viii) The mean dobEF is negatively associated with the recent bypass surgery (yes=0, no=1) newCABG (P=0.0049), indicating that the dobEF is higher of the cardiac patients with DSE who have newCABG.
(ix) The mean dobEF is negatively associated with the history of smoking (non-smoker=0, moderate=1, heavy=2) hxofCig (P=0.0261), indicating that the dobEF is lower of the cardiac patients with DSE who have heavy smoking status.
(x) The variance of dobEF is positively associated with the posSE (P=0.0285), indicating that the dobEF variance is higher of the cardiac patients with DSE who have no posSE.
(xi) The dobEF variance is negatively associated with the dobdose (P=0.0015), indicating that the dobEF variance increases as the dobdose decreases.
(xii) The dobEF variance is negatively associated with the baseEF (P<0.001), indicating that the dobEF variance increases as the baseEF decreases. Note that the baseEF variance also satisfies the same association with the dobEF, and also the mean and variance relationships between the baseEF and the dobEF are identical.
Discussion
The present report has identified many determinants of the baseline ejection fraction and also the ejection fraction on dobutamine (Results and interpretation Sections) of UCLA stress echocardiography data. In both cases, the gamma fitted model gives better results than the lognormal (not shown here), so only the gamma model results are displayed herein. One can verify the present results examining the data set given in (https://www.stat.ucla.edu:16080/projects/datasets/cardiacexplanation.html). To the best of our knowledge, most of these derived results (Result and interpretation Sections) are new in hypertension literature with DSE. Specially, all the findings of the variance model are completely new. The present analyses have derived many interaction effects, which focus most probably the real practical situations.
In the present analyses, it is observed that the some mean predicting parameters of baseEF and dobEF are common (Tables 3 and 4). The common mean predicting parameters of both baseEF and dobEF are sbp, dp, dose, posSE, newPTCA and hxofCig. But their effects are completely different on the dobEF than the baseEF. For example, sbp and posSE are positively associated with the baseEF, while they are inversely associated with dobEF. Similarly, dp, dose and newPTCA are negatively associated with the baseEF, but they are positively associated with the dobEF. Again hxofCig is positive insignificantly associated with the baseEF, while it is negative significantly associated with the dobEF. But for the variance predicting common parameter of both baseEF and dobEF is hxofCABG (Tables 3 and 4), which has the same effect on both the ejection fractions.
The present findings of baseEF and dobEF analyses are described in the results and interpretations sections. In the present analyses, age and sex are insignificant effects of both the baseEF and dobEF, but age is insignificant and sex is significant effect in the earlier analyses [16,17]. Smoking is significant in the current dobEF analysis, but it is insignificant of LVEF [17]. Systolic blood pressure (sbp) is significant in the current both the baseEF and dobEF analyses, and it is also significant of RVEF and LVEF [16,17]. To the best of our knowledge, it is the first article which has considered the joint mean and variance effects of baseEF and dobEF. Moreover, many new factors (Tables 3,4) are identified as significant effects of baseEF and dobEF in the current analyses, which are not discussed in the earlier articles.
The current report tries to fill some gaps of the hypertension literature by deriving the present results (Tables 3 and 4), which illuminate the complex relationships. Fortunately, a true mathematical model can open the truth that is covered by the complex relationships. Our research had two purposes. The first was to compare our results to those of previous research. A second purpose was to evaluate the statistical assumptions made by previous research regarding the cardiac ejection fraction determinants. Our concern was that previous research, making some inappropriate assumptions, would draw important conclusions from erroneous assumptions. As the given data set is positive heterogeneous, so only the gamma JGLM results are displayed, based on comparison with the log-normal (not shown). The present reported results, though not completely conclusive, are revealing:-
The present results have been derived based on five criteria. First, is the comparison of both the log-normal and gamma models. Second, is the smallest AIC. Third, is very small standard deviation of the estimates (Tables 3 and 4), consequently, they are stable [19]. Fourth, are the regression diagnostic checks by graphical analysis. Fifth, is the locating the appropriate dependent variable distribution.
These findings confirm some previous research findings, and they also try to remove some conflicts of earlier research findings. This can be observed on comparison of the present results (Table 3 and 4) with the Tables 1-3 of [7,16,17].
An important conclusion has to do with the use of earlier used statistical models. While further research is called for, we find that the gamma JGLMs are much more effective than either joint log-normal or multivariate regression analysis, because they better fit the data. In short, research should have greater faith in these results than those emanating from the earlier models.
The findings of the present analyses along with the effects are described in result and interpretation sections. Medical practitioners and cardiac patients will be benefited from these findings. Even though these findings are related with the DSE data set, yet the present report recommends the following for all individuals. For an appropriate medical treatment, cardiac events, the amount of dobutamine dose and its interaction effects, and the history of the disease should be considered by the medical practitioners (Tables 3 and 4). Cardiac patients should be aware of the effects of cardiac events and their history. Smoking should be stopped (Table 4).
Acknowledgement
The author is very much indebted to the referees who have provided valuable comments to improve the paper. The author thanks Dr. Alan Garfinkel, UCLA School of Medicine, Department of Physiology, Los Angeles, California, USA, who generously provided the data sets to freely distribute and use for non-commercial purposes.
References
- Kumar V, Abbas AK, Aster J (2009) Robbins Cotran pathologic basis of disease. St. Louis, Mo: Elsevier Saunders.
- Maceira A (2006) Reference right ventricular systolic and diastolic function normalized to age, gender and body surface area from steady-state free precession cardiovascular magnetic resonance. Euro Heart J 27: 2879-2888.
- Maceira A (2006) Normalized left ventricular systolic and diastolic function by steady state free precession cardiovascular magnetic resonance. J cardiovas mag reso 8: 417-426.
- Kitzman DW, Higginbotham MB, Cobb FR, Sheikh KH, Sullivan MJ (1991) Exericise intolerance in patients with heart failure and preserved left ventricular systolic function failure of the Frank-Starling mechanism. J Am Coll Cardiol 17: 1065-1072.
- Vasan RS, Larson MG, Benjamin EJ, Evans JC, Reiss CK, et al. (1999) Congestive heart failure in subjects with normal versus reduced left ventricular ejection fraction: Prevalence and mortality in a population based cohort. J Am Coll Cardiol 33: 1948-1955.
- Maeder MT, Kaye DM (2009) Heart failure with normal left ventricular ejection fraction. J Amer Coll Cardio 53: 905-918.
- Ndrepepa G, Mehilli J, Martinoff S, Schwaiger M, Schoming A, et al. (2007) Evolution of left ventricular ejection fraction and its relationship to infract size after acute myocardial infraction. J Am Coll Cariol 50: 149-156.
- Bruyne BD, Heyndrickx GR (2007) Changes in infract size and left ventricular ejection fraction. J Am Coll Cariol 50: 157-158.
- Zile MR, Lewinter MM (2007) Left ventricular end-diastolic volume is normal in patients with heart failure and a normal ejection fraction: A reviewed consensus in diastolic heart failure. J Am Coll Cariol 49: 982-985.
- Owan TE, Hodge DO, Herges RM, Jacobsen SJ, Roger VL, et al. (2006) Trends in prevalence and outcomes of heart failure with preserved ejection fraction. N Eng J Med 355: 251-259.
- Sanderson JE (2007) Heart failure with a normal ejection fraction. Heart 93: 155-158.
- Simone G, Gottdiener JS, Chinali M, Maurer MS (2008) Left ventricular mass predicts heart failure not related to previous myocardial infraction: The cardiovascular heart study. Eur Heart J 29: 741-747.
- Marin JM, Carrizo SJ, Vicente E, Agusti AG (2005) Long-term cardiovascular outcomes in men with obstructive sleep apnoea-hypopnoea with or without treatment with continuous positive airway pressure: An observational study. Lancet 365: 1045-1053.
- Borlaug BA, Kass DA (2006) Mechanisms of diastolic dysfunction in heart failure. Trend Cardiovasc Med 16: 273-279.
- Kawut SM, Al-Naamani N, Agerstrand C, Rosenzweig EB, Rowan C, et al. (2009) Determinants of right ventricular ejection fraction in pulmonary arterial hypertension. Chest 135: 752-759.
- Jazi MH, Nilforoush P, Gharipour M, Batvandi A, Mohammadi R, et al. (2015) Clinical determinants of left ventricular ejection fraction deterioration in patients suffered from complete left bundle branch block. Iran Red Cres Med 17: 16570.
- Myers RH, Montgomery DC, Vining GG (2002) Generalized linear models with applications in engineering and the sciences. J Wil Son.
- Lee Y, Nelder JA, Pawitan Y (2006) Generalized linear models with random effects (Unified Analysis via H-likelihood). Chap Hal.
- Myers RH, Carter WH (1973) Response surface techniques for dual response systems. Techno 15: 301-317.
- Das RN, Lee Y (2010) Analysis strategies for multiple responses in quality improvement experiments. Int J Qual Eng Techno 1: 395-409.
- Firth D (1988) Multiplicative errors: Log-normal or gamma. J R Statist Soc B 50: 266-268.
- Das RN, Park JS (2012) Discrepancy in regression estimates between log-normal and gamma: Some case studies. J App Stat 39: 97-111.
- Krivokapich J, Child JS, Walter DO, Garfinkel A (1999) Prognostic value of dobutamine stress echocardiography in predicting cardiac events in patients with known or suspected coronary artery disease. J Amer Col Cardio 33: 708-716.
- Das RN, Lee Y (2009) Log normal versus gamma models for analyzing data from quality-improvement experiments. Qual Eng 21: 79-87.
- Nelder JA, Lee Y (1991) Generalized linear models for the analysis of Taguchi-type experiments. App Stoc Mod Data Anal 7: 107-120.
- Marcovitz PA, Armstrong WF (1992) Accuracy of dobutamine stress echocardiography in detecting coronary artery disease. Am J Cardiol 69: 1269-1273.
- Davila-Roman VG, Waggoner AD, Sicard GA, Geltman EM, Schechtman KB, et al. (1993) Dobutamine stress echocardiography predicts surgical outcome in patients with an aortic aneurysm and peripheral vascular disease. J Am Coll Cardiol 21: 957-963.
- Secknus MA, Marwick TH (1997) Evolution of dobutamine echocardiography protocols and indications: safety and side effects in 3,011 studies over 5 years. J Am Coll Cardiol 29: 1234-1240.
- Das RN (2014) Robust response surfaces, regression, and positive data analyses. Chap Hall.
- Hastie T, Tibshirani R, Friedman J (2001) The Elements of Statistical Learning. Springer.
Citation: Das RN (2017) Determinants of Cardiac Ejection Fraction for the Patients with Dobutamine Stress Echocardiography. Epidemiology (Sunnyvale) 7:307.
Copyright: © 2017 Das RN, This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Select your language of interest to view the total content in your interested language
Share This Article
Recommended Journals
Open Access Journals
Article Usage
- Total views: 5044
- [From(publication date): 0-2017 - Sep 03, 2025]
- Breakdown by view type
- HTML page views: 4131
- PDF downloads: 913