Research Article Open Access
Fractal Analysis of Pre-Seismic Electromagnetic and Radon Precursors: A Systematic Approach
Nikolopoulos D1*, Petraki E1, Cantzos D2, Yannakopoulos P1, Panagiotaras D3, Nomicos D41Department of Electronic Computer Systems Engineering, Piraeus University of Applied Sciences, Petrou Ralli and Thivon 250, GR-12244 Aigaleo, Greece
2Department of Automation Engineering, Piraeus University of Applied Sciences, Petrou Ralli and Thivon 250, GR-12244 Aigaleo, Greece
3Department of Mechanical Engineering, Technological Educational Institute (TEI) of Western Greece, M. Alexandrou 1, 263 34 Patras, Greece
4TEI of Athens, Department of Electronic Engineering, Agiou Spyridonos, GR-12243, Aigaleo, Greece
- *Corresponding Author:
- Nikolopoulos D
Department of Electronic Computer Systems Engineering
Piraeus University of Applied Sciences
Petrou Ralli and Thivon 250
GR-12244 Aigaleo, Greece
Tel: 210-5381100
E-mail: dniko@teipir.gr
Received date: September 15, 2016; Accepted date: November 15, 2016; Published date: November 19, 2016
Citation: Nikolopoulos D, Petraki E, Cantzos D, Yannakopoulos P, Panagiotaras D et al. (2016) Fractal Analysis of Pre-Seismic Electromagnetic and Radon Precursors: A Systematic Approach. J Earth Sci Clim Change 7: 376. doi: 10.4172/2157-7617.1000376
Copyright: © 2016 Nikolopoulos D, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Journal of Earth Science & Climatic Change
Abstract
This paper reports characteristic pre-seismic disturbances of electromagnetic radiation of the MHz range and of radon in soil. All the disturbances were collected in an organised manner from a telemetric network operating in Greece in a period of five distinct years during which a total of thirty seven earthquakes occurred. This study includes thirty-three pre-seismic MHz electromagnetic disturbances with duration of a few days up to one month and four lengthy radon precursors, all recorded prior to earthquakes that occurred in years 2007, 2008, 2009, 2014, 2015 with M L ≥ 5.0. The paper is a systematic investigation of the outputs of the fractal analysis from the thirty seven earthquakes. The results indicated that the majority of the investigated signals (both electromagnetic radiation and radon) exhibited characteristic epochs with fractal organisation. Continuous epochs were detected in several one-month, electromagnetic radiation, signals. As fractal epochs were considered those with successive (r2 ≥ 0.95) power-law behaviour and b - exponent in the fBm class (1 ≤ b ≤ 3). As enhanced precursory fractal epochs were considered the successive fBm ones with many successive (r2 ≥ 0.95) segments above 1.5 with extra attention given to the ones above 2.0. These epochs indicated well-established long-memory dynamics well away from fGn randomness. Several successive ( r2 ≥ 0.95) fractal electromagnetic and radon segments showed anti-persistency (1.5 ≤ b < 2.0). Nevertheless, numerous persistent ( 2.0 < b ≤ 3.0 ) parts were detected. Switching between persistency and anti-persistency was identified. This switching was considered of enhanced precursory value of the electromagnetic and radon signals. The findings indicated selforganised critical state characteristics of the last stages of the investigated earthquakes. It was concluded that the fractal analysis can be employed as a first screening method for the identification of long-memory patterns hidden in pre-seismic time-series. The method is reliable in identifying pre-earthquake patterns.
Keywords
Earth; Electromagnetic radiation; Radon; Fractals; Earthquakes
Introduction
It is well accepted within the earthquake scientific community that several electromagnetic (EM) phenomena have been recognised as seismic precursors, viz., they are recorded prior to significant earthquakes. The EM seismic precursors include ultra-low frequencies (ULF) from 0.001 to 1 Hz [1-7], low frequencies (LF) from 1 to 10 kHz [6,8-13], high frequencies (HF) from 40 to 60 MHz [6,8,14- 17] and very high frequencies (VHF) up to 300 MHz [18]. A key strategy for recognising the EM pre-earthquake precursors is the direct detection of EM radiation emission from the lithosphere [5]. A significant alternative is the indirect detection of seismic effects that take place in a form of propagation of an EM anomaly due to existing transmitter signals [5]. The idea is that the EM disturbances emerge out of the hypocentre of the earthquakes because of various tectonic displacements [5]. Investigators have indicated that the principal EM transmitters are within the earth's crust [6]. As indicated by researchers [10,11,19], these principal transmitters are the dynamically unstable multi-cracks that are continuously generated and moved during the earthquake preparation process. It is the movement of the cracks that causes the fragment of the ionic bonds at the surfaces of new small scale cracks and brings out the surface-charge division which transforms the smaller scale cracks into effective electric dipoles and electromagnetic emitters before seismic events [9-11,20,21]. Therefore, the study of EM precursors is a significant step towards reliable earthquake prediction.
Apart from the EM precursors, radon has also been utilised extensively for the prognosis of earthquakes. As it is well known, radon-222 (hereafter radon) is a natural noble radioactive gas that is generated by the decay of radium-226. Being almost chemically inactive, radon migrates from the region of its generation and can be easily detected even at low levels [22-24]. Radon is naturally released from the soil and approximately 10% of it, is diluted in the atmosphere [22-24]. Apart from soil, radon is present in fragmented rocks, building materials, underground and surface waters [23,24]. While in fluids all the generated radon atoms are diluted, in the porous media and the fragmented rocks, only a percentage of radon emanates, enters the volume of the pores and dissolves into the pore's fluid [22,24]. However, once there, a macroscopic transport is possible via molecular diffusion, advection or convection [22]. This transport is achieved through the interconnected pores of the underlying soil, as well as, via the water aquifers [24-26]. When the pores are saturated with water, radon is dissolved into the water and is transported by it [22]. The transportation is implemented through flow of fluids that are present in the soil and the fragmented rocks [22,24-26]. Through these processes radon can be detected in short, medium or long distances from its generation, either in the water aquifers or air [27,28]. Noteworthy variations of the concentration of radon and progeny have been observed in geothermal fields [29], thermal spas [30], active faults [31-35], soil experiments [36], volcanic processes [37,38] and seismotectonic environments [16,21,25,27,36,39-46]. Due to its importance, radon monitoring is also a significant study area in the search of premonitory signals prior to earthquakes [25]. In the following analysis, results from the spectral fractal analysis of electromagnetic time-series of the MHz range and radon time signals are presented. By looking into the fractal characteristics concealed in both MHz electromagnetic and radon time-series, the examination endeavours to explore potential relationships of the outcomes with thirty seven earthquakes. The earthquakes happened in Greece between years 2007 and 2015 and had local magnitudes of M L ≥ 5.0. Most of the investigated time-series showed various parts connected with long-memory behaviour. These instances are considered to be tied with the characteristic conditions of the last phases of the preparation of the explored events. The results demonstrate that fractal analysis accomplishes to identify effectively if the signal is modelled satisfactorily as fractional Brownian motion (fBm). The precursory value of the signals is also discussed.
Materials and Methods
Theoretical aspects
Rather than describing a procedure in the time domain, it is often preferable to describe it in the frequency domain [47,48]. This approach has numerous applications in physics, time series analysis, investigation of pre-earthquake signals etc. A significant tool for the analysis in the frequency domain is the Fourier transform. The Fourier transform can modify a time function, w(t),from the time to the frequency domains without any loss of information:
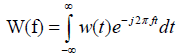 (1)
(1)
The inverse Fourier transform can reproduce the time function from its frequency-domain representation [47,48]:
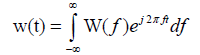 (2)
(2)
According to the Fourier transform, a physical signal can be examined through its decomposition into a linear combination of sinusoidal functions of different frequencies. These frequency components describe the signal completely by means of the amount in which each frequency component contributes to the signal [48]. The power spectral density (PSD) gives information concerning to which extend each frequency is present in the signal [47,48].
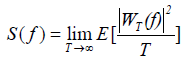 (3)
(3)
With WT(f) the truncated Fourier transform, given as 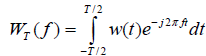 . In various cases the PSD is linked with the so-called 1/ f processes. The 1/f processes are self-similar procedures which model an extensive variety of natural signals [49]. They are procedures which are characterised as having PSD complying with a power law relationship of the form
. In various cases the PSD is linked with the so-called 1/ f processes. The 1/f processes are self-similar procedures which model an extensive variety of natural signals [49]. They are procedures which are characterised as having PSD complying with a power law relationship of the form
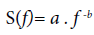 (4)
(4)
where b is the spectral fractal parameter connected with the parameter H given by the relation:
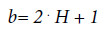 (5)
(5)
Η is a self-similarity parameter of the procedure which is widely known as Hurst exponent [49,50].
The most well-known models for 1/ f processes are the fBm and the fGn. In the work of Mandelbrot and Van Ness [51], the fBm procedures are the ones related to PSD exponents of 1< b < 3. The Brownian motion is a case corresponding to b = 2 [48,51]. Conversely, forms related to exponents of − 1< b <1 are fractional Gaussian noises and stationary Gaussian noise is the exceptional case corresponding to b = 0 [49]. The theory does not straightforwardly include the cases of b > 3 and b < −1 and, moreover, does not operate well for the cases b = 1, b = −1 and b = 3 [49].
Regarding the fBm class, this is defined by its stochastic representation
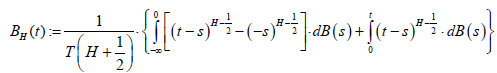 (6)
(6)
where Γ is the Gamma function
 (7)
(7)
0 < H <1 is the Hurst exponent and B is the so-called ordinary Brownian motion. It is essential to note here that the fBm classes are, in point of fact, fractals. More specifically, fBm models have selfsimilarity parameters in the range of 0 < H <1 (i.e. 1< b < 3) and a fractal dimension of D = 2 - H which, importantly, is a measure of their roughness [49].
On the other hand, an incremental process, X , is defined as fGn when it follows the relation
 (8)
(8)
where Xt has a normal distribution for every t [50]. For 1/ 2 < H <1 the fGn process demonstrates persistent correlation structure, for H = 1/ 2 it has no correlation, whereas for 0 < H < 1/ 2 it demonstrates persistent anti-correlation [49].
Especially regarding signals recorded prior to earthquakes and according to [3,4,10,11,16,27,43,51], a series of steps in the lithosphere linked in time and space, constitute the complex process of earthquake preparation. These linkages produce characteristic fractal structures which affect electromagnetic and soil-radon disorders emitted from the lithosphere during seismic activity [3,4,10,11,16,27,43,51]. The power spectral density, S (f), is likely the most often utilised method to give helpful information about the inherent memory and the critical behaviour of the system [3,4,10,11,16,27,43,51]. Furthermore, the power spectrum reflects directly the physical scales of the processes that affect the structure formation [10].
Fractal analysis
If a time series A(ti) is a temporal fractal, then the spectrum follows a power-law S (f )= a . f -b ,where f is the frequency of the transform. The log (S (f ))- log (f ) representation of the power spectrum is a straight line with slope b . The amplification a quantifies the power of the spectral components following the power law and the spectral scaling exponent b is a measure of the strength of time correlations. It is significant to recognise areas in the signals with distinct changes of the scaling exponent b, since such changes are reported to emerge [10,11,16,17,27,43,44] before or during anomalies in the EM radiation or in the concentration of radon in soil. Accounting these facts, several lengthy EM and radon signals were analysed in this paper, to identify segments with distinct changes of the PSD exponent b . Note, that the fBm class has been linked to pre-earthquake activity of noteworthy precursory value and, especially, in the high b segments. For the analysis, all the studied EM and radon signals were investigated through fractal analysis [10,11,16,17,27,43,44] based on a waveletderived PSD. To calculate the PSD of this study, the continuous wavelet transform (CWT) was used with the Morlet wavelet as a base function. The goodness of the power-law fit of the PSD of the investigated timeseries was analysed through the square of the Spearman's correlation coefficient following similar analysis as in [16,17,27,43,44]. In specific the following steps were followed:
(i) The MHz EM and the radon signals were divided in segments (windows). More specifically, 1024 samples per segment were used for the EM signals and 128-512 samples per segment for radon. These divisions-segmentations were expected to reveal the fractality of the signals [10,11,16,17,27,43,44].
(ii) In each segment the PSD of the signal was calculated. As aforementioned, for the PSD calculation, the CWT using the Morlet wavelet was employed.
(iii) In each segment the existence of a power-law of the form of 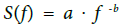 was investigated. In the CWT PSD calculation, the employed frequency f was the central frequency of the Fourier transform of each Morlet scale.
was investigated. In the CWT PSD calculation, the employed frequency f was the central frequency of the Fourier transform of each Morlet scale.
(iv) The least square method was applied to the log(S(f ))- log(f) linear representation. Successive representations were considered those that exhibited squares of the Spearman's correlation coefficient above 0.95.
Seismicity of the investigated time-period (2007-2015)- Criteria for the selection of the investigated earthquakes
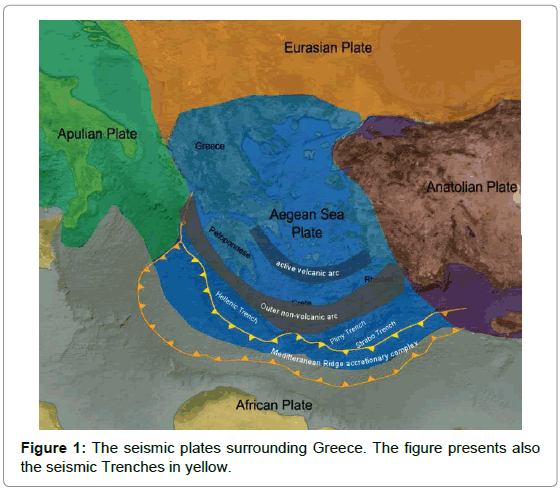
Greece lies on the boundary convergence of the Eurasian and African plates, on two micro-plates: the Aegean Sea Plate and the Anatolian Plate. Therefore, Greece is inclined to earthquakes since it is traversed by the convergence of the two aforementioned plates and the western zone of the North Anatolian Fault (Figure 1). The country is dominated by extensive seismicity structures and numerous active faults of complex active stress field. The seismicity structures of Greece evoked several earthquakes of M L ≥ 5.0 during the last century. During the period of the analysis of this research, i.e., between January 2007 and May 2015, several earthquakes occurred in Greece and near areas with local magnitudes M L ≥ 5.0 and with depths ranging from 2 km to 165 km. Thirty seven of these events were analysed in this paper. The total number of the events with M L ≥ 5.0 between 2007 and 2015, the number of the analysed events through fractal analysis and the succeeded rate of the analysis of the actual events are presented in Table 1.
| Year | Number of earthquakes with M L ≥ 5.0 | Analysed events | Rate of the analysed events |
|---|---|---|---|
| 2007 | 7 | 4 | 57.00% |
| 2008 | 20 | 12 | 60.00% |
| 2009 | 10 | 9 | 90.00% |
| 2013 | 8 | 3 | 37.50% |
| 2014 | 12 | 6 | 50.00% |
| 2015 | 3 | 3 | 100% |
Table 1: Number of earthquakes between 2007 and 2015 with M L ≥ 5.0, number of events analysed via fractal analysis and succeeded rates.
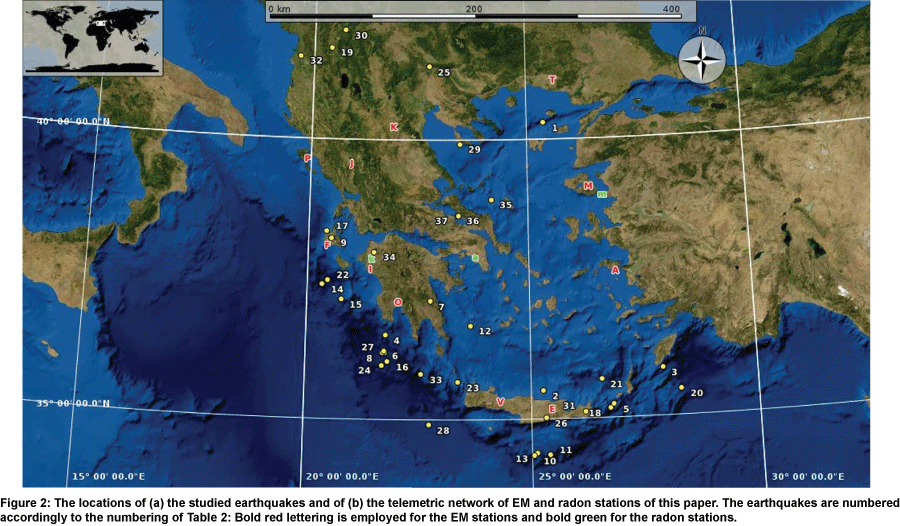
It becomes evident from Table 1 that the earthquakes analysed with fractal methods had local magnitudes of M L ≥ 5.0. The M L = 5.0 threshold was selected as a characteristic critical risk levelcompensating between the catastrophic potential of an earthquake, the interest of the Hellenic State and the public and the usefulness of focusing the investigation on a noteworthy number of earthquakes with scientific concern. A percentage of 67.5% of the events of Table 1 occurred in the Hellenic Trench. As can be observed from Figure 1, the Hellenic Trench is developed in the western part of the Hellenic Arc which is an area of great seismicity. This fact adds scientific value in the investigation of these earthquakes. On the other hand, the remaining seismic events of Table 1 occurred in the other two main seismic plates that surround Greece, viz., the Anatolian and Aegean Plates. In specific, 5.5% of the events occurred near the Anatolian Plate and the remaining 27%, in the Aegean Plate. As can be observed from Table 1, the investigated events were more than 50% of the occurred ones for all the years except 2013. This marks up a fairly good proportion for the implemented analysis with fractals. It should be emphasised that this is the first study of this range, viz. it is the first study with this amount of analysed events. As will be described in the reviews of [5,52-54], the majority of the earthquake related papers are limited to one event or few events (mainly of low magnitudes and, in the majority of cases, scattered in space and time). Especially for the case of Greece, the majority of papers (more than 60) referred to three great earthquakes and especially the Pyrgos earthquake (1993), the Kozani-Grevena earthquake (1995) and the Athens earthquake (1999). In comparison, this paper includes nine great earthquakes with M L ≥ 6.0 and the remaining twenty seven events with 5.0 ≤ M L < 6.0 . It should be noted though, that this paper includes also the re-analysis of some earthquake raw data published in other papers of the reporting team [16,27,43,44,55-58], however, under a different view and with new approach. It can be, thus, supported, that either from the view of great earthquakes ( M L ≥ 6.0 ) or the perspective of the number of the analysed events (37), this research includes a significant amount of seismic data. Table 2 presents the partial data of the analysed earthquakes and Figure 2 depicts their corresponding locations. The earthquakes with event number 1-33 were analysed through MHz time-series and the earthquakes from 34 to 37 through radon time-series. The numbering of the earthquakes of Table 2 is used in Figure 2 as well and will be used hereafter as a reference to the aforementioned earthquakes.
| Event | Date | Location | Lat. (0N) | Long. (0E) | Depth (km) | ML |
|---|---|---|---|---|---|---|
| 1 | 24-05-2014 | 22.9 km SSW of Samothraki | 40.29 | 25.4 | 28 | 6.3 |
| 2 | 12-10-2013 | 66.6 km W of Chania | 35.5 | 23.28 | 65 | 6.2 |
| 3 | 15-07-2008 | 71.1 km SSW of Rhodes | 35.85 | 27.92 | 56 | 6.2 |
| 4 | 14-02-2008 | 35.9 km SSE of Methoni | 36.5 | 21.78 | 41 | 6.2 |
| 5 | 16-04-2015 | 56.7 km SSW of Karpathos | 35.23 | 26.82 | 37 | 6.1 |
| 6 | 14-02-2008 | 66.5 km S of Methoni | 36.22 | 21.75 | 38 | 6.1 |
| 7 | 06-01-2008 | 9.3 km SW of Leonidion | 37.11 | 22.78 | 86 | 6.1 |
| 8 | 20-02-2008 | 70.8 km S of Methoni | 36.18 | 21.72 | 25 | 6 |
| 9 | 26-01-2014 | 6.7 km NE of Argostoli | 38.22 | 20.53 | 21 | 5.8 |
| 10 | 15-06-2013 | 109.7 km S of Iraklion | 34.34 | 25.06 | 32 | 5.8 |
| 11 | 01-07-2009 | 111.2 km SSE of Iraklion | 34.35 | 25.4 | 30 | 5.8 |
| 12 | 29-08-2014 | 69.4 km W of Milos | 36.67 | 23.67 | 97 | 5.7 |
| 13 | 16-06-2013 | 116.2 km S of Iraklion | 34.28 | 25.13 | 28 | 5.6 |
| 14 | 03-11-2009 | 65.6 km SW of Zakynthos | 37.39 | 20.35 | 39 | 5.6 |
| 15 | 16-02-2009 | 74.2 km S of Zakynthos | 37.13 | 20.78 | 15 | 5.5 |
| 16 | 21-06-2008 | 88.2 km S of Methoni | 36.03 | 21.83 | 12 | 5.5 |
| 17 | 25-03-2007 | 19.3 km NNW of Argostoli | 38.34 | 20.42 | 15 | 5.5 |
| 18 | 17-04-2015 | 67.2 km SSW of Karpathos | 35.16 | 26.74 | 40 | 5.4 |
| 19 | 06-09-2009 | 124.6 km NW of Florina | 41.62 | 20.41 | 10 | 5.4 |
| 20 | 19-06-2009 | 107.8 km ESE of Karpathos | 35.46 | 28.31 | 42 | 5.4 |
| 21 | 27-03-2015 | 52.9 km W of Karpathos | 35.68 | 26.82 | 37 | 5.3 |
| 22 | 11-11-2009 | 51.8 km SW of Zakynthos | 37.47 | 20.47 | 21 | 5.3 |
| 23 | 13-01-2009 | 68.2 km W of Karpathos | 35.66 | 26.39 | 42 | 5.2 |
| 24 | 26-02-2008 | 95.3 km S of Methoni | 35.96 | 21.7 | 5 | 5.2 |
| 25 | 24-05-2009 | 36.0 km NNW of Kilkis | 41.3 | 22.74 | 23 | 5.1 |
| 26 | 28-03-2008 | 39.4 km SSE of Iraklion | 35.01 | 25.33 | 50 | 5.1 |
| 27 | 19-02-2008 | 70.0 km S of Methoni | 36.19 | 21.77 | 22 | 5.1 |
| 28 | 28-01-2007 | 133.6 km WSW of Chania | 34.9 | 22.75 | 34 | 5.1 |
| 29 | 22-08-2014 | 50.6 km S of Poliyiros | 39.92 | 23.46 | 29 | 5 |
| 30 | 08-01-2009 | 139.9 km NNW of Florina | 41.94 | 20.74 | 2 | 5 |
| 31 | 12-06-2008 | 99.2 km ESE of Iraklion | 35.11 | 26.19 | 29 | 5 |
| 32 | 16-04-2007 | 162.5 km WNW of Florina | 41.46 | 19.68 | 5 | 5 |
| 33 | 03-02-2007 | 63.8 km SW of Kithira | 35.8 | 22.58 | 99 | 5 |
| 34 | 08-06-2008 | 23.1 km ENE Andravida | 37.98 | 21.51 | 25 | 6.5 |
| 35 | 19-03-2008 | 34.1 km W of Skyros | 38.92 | 24.17 | 35 | 5 |
| 36 | 17-11-2014 | 25.6 km NW of Chalkida | 38.64 | 23.41 | 23 | 5.2 |
| 37 | 17-11-2014 | 26.2 km NW of Chalkida | 38.64 | 23.4 | 24 | 5.2 |
Table 2: List of seismic events investigated with fractal analysis. In descending local magnitudes (ML). Lat, Long and Depth are the latitude, longitude and depth of the epicentre of the earthquake.
Significance of the analysed earthquakes
Following the reviews of [5,52,53], and [54], the short term electromagnetic earthquake precursors are promising tools for the prediction of earthquakes. In general, it is well accepted that electromagnetic phenomena are detectable before the occurrence of earthquakes [3,4,9,10,18]. [5] reported that several seismogenic phenomena have already been found from direct current (DC), ULF up to VHF. According to [52], most of the electromagnetic precursors are in the ULF and LF ranges [4,59-63]. Additionally, since 1980, a small number of scientific papers have been published which made use of the MHz electromagnetic precursors in an effort to predict earthquakes [8,14,64-69]. This paper, as the related papers of the reporting team [16,17,27,56], adopts this view and presents the re-analysis of MHz electromagnetic signals of 33 seismic events from 2007 to 2015 in Greece through chaotic fractal methods. The adopted high frequencies (41 MHz & 46 MHz) have advantages over the ULF and LF emissions. For example, the electric and magnetic antennas that detect ULF, perform usually in shallow depths and hence the recordings contain, frequently, electromagnetic noise. Moreover, due to their installation position, they are often destructed by agricultural activities, thunderstorms and other reasons. In addition, the LF emissions of the kHz range have been employed only in few cases (Kozani-Grevena, Athina and L'Aquila earthquakes) as seismic precursors. Despite the great research and argumentation [6,10-13,70,71], the few detected signals still restrict the results and set them under scientific debate. Note that, based on several arguments, the investigators of these papers claim that the detected kHz anomalies refer to the inevitable last phase of the earthquake evolution. On the contrary to the ULF and LF emissions, the HF MHz radiation has low to medium electromagnetic noise and, hence, higher prediction ability [14,16,17]. In the following sections, further arguments will be provided regarding the predictability of the MHz precursors especially when combined with the continuous recordings of radon in soil.
As regards to radon precursors, according to the review of [72], the related studies have shown that noteworthy geophysical and geochemical changes can occur before earthquakes, with the more intense being the changes of the concentration of gases and, especially, soil radon. It is very important that the bulk of the experiments reported in the gas related pre-seismic scientific literature have focused on radon [21]. According to [16,27,40,43,44,56,73] a radon anomaly acts as a precursor of a seismic event. Radon concentration may alter (increase or decrease) significantly before earthquakes in a manner that it cannot be attributed to the diurnal or meteorological variations [74]. As reported by [52], from 1969 to 2014 the earthquakes with M L ≥ 5.0 with related recorded radon emissions, were about fifty worldwide. In this view, the three of these worldwide events [16,27,43] that are re-analysed in this paper, make an important point and, especially because one of these [27] (earthquake 33, Table 2), corresponded to an earthquake of M L = 6.5. Taking into account that the magnitude and the duration of a radon anomaly depend on the distance of the observation site to the earthquake epicentre and the magnitude of the event [21] and that the greatest anomalies were reported at the closest distance to the epicentres of the forthcoming earthquakes [21], the Ileia M L = 6.5 pre-earthquake radon anomalies [16,27,43] which were recorded only 29 km away from the epicentre of the earthquake, makes the present paper more significant. Note, that it is very rare to address the coincidence or the vicinity between recordings of an observation site and the epicentre of a large earthquake. This explains why radon signals with great anomalies and long duration are very rare in the literature. Most importantly, according to [16,27,43,44] , the radon anomalies of the earthquake 33 of Table 2, were not detected only with active techniques but also through passive ones. It is significant to note also, that in the radon related earthquake literature, the methods that are used for processing the radon signals are, mostly, statistical or visual [46,75-79].
Instrumentation
MHz antennas: The MHz electromagnetic signals were continuously monitored by a telemetric network, consisting of 12 stations [80]. These stations are now located in the following seismic regions: (1) Ithomi (O), Peloponnese, (2) Valsamata (F), Kefalonia Island, (3) Ioannina (J), (4) Kozani (K), (5) Komotini (T), (6) Kalloni (M), Lesvos Island, (7) Rhodes (A), Rhodes Island, (8) Neapolis (E), Crete Island, (9) Vamos (V), Crete Island, (10) Corfu (P), Corfu Island, (11) Ileia (I), Peloponnese and (12) Atalanti (H). Stations 1, 2, 9, 10 and 11 are located along the Hellenic Trench. Stations 5, 6, 7 are located in the vicinity of the Anatolian Plate and stations 3, 4, 8 are located in the wider area of the Aegean Plate. The locations of the EM stations are shown in Figure 2 with the corresponding lettering in bold red. Each station comprises (1) bipolar antennas synchronized at 41 and 46 MHz; (2) novel acquisition data-loggers [81] and (3) telemetry equipment (e.g. RF modem-wired or cordless internet).
Apparatus for radon measurements
Alpha guard: The active techniques utilised Alpha Guard (AG), Genitron Ltd. AG equipped with a soil gas unit (Genitron Ltd.) which consists of an 1m probe, a gas tight pump (Alpha Pump) and accompanying equipment [82]. The AG probe was immersed 1m below the ground to minimise the meteorological influences [25,83]. Soil gas was pumped at the maximum available rate of 1L . min-1 [82] for maximising the gas quantity and enhancing the detection efficiency. The gas was driven into the AG through an input flow adapter where it was measured at the rate of 1 measurement per 10 min. The pumped gas escaped the AG through an output flow adapter. Atmospheric pressure (AP), relative humidity (RH) and temperature (T) were continuously monitored as well [82]. The whole set-up was connected to a PC which handled the AG through its licensed software (AVIEW) [82]. The whole operation of the AG (including data manipulation and transfer) was remotely controlled through a secured internet connection. The overall system (AG, host-remote computer, remote control-operation) constituted the AG radon-telemetry station. The measurements derived from Alpha Guard and re-analysed in this study, were recorded from two radon-telemetry stations. These two stations were established in Kardamas, Ileia, Peloponnese (k, Figure 2) and in Mytilene in Lesvos Island (m, Figure 2).
Barasol MC2: Active radon measurements were conducted also with the VDG Baracol (ALGADE, France) unit which was installed in the Campus of Technological Educational Institution of Athens (a, Figure 2). Radon in soil was monitored by the radon probe Barasol MC2 (BMC2 and accessed through a telemetric station. The main quantities measured by the BMC2 probe were the concentration of 222Rn, the temperature and the atmospheric pressure. For the measurement, the BMC2 sensor (implanted silicon detector) achieved the counting of atoms of 222Rn and progeny by spectrometry. The instrument is designed for the use in difficult environments and to collect passive measurements not disturbing the nearby environment. For the monitoring purposes, the BMC2 probe was installed in a borehole at 1m depth and the radon in soil was sampled at the rate of 1 measurement per 15 minutes. This radon telemetric station comprises also a solar panel, an IEEE box with all the electronic equipment and the telemetric 3G emitting instrumentation. Figure 2 shows also the network of the radon stations in Greece. As aforementioned, the network comprises of 3 stations: the Ileia (k) station operating with Alpha Guard, the Lesvos station (m) with Alpha Guard and the Athens station (a) operating with the VDG Barasol unit.
Results and Discussion
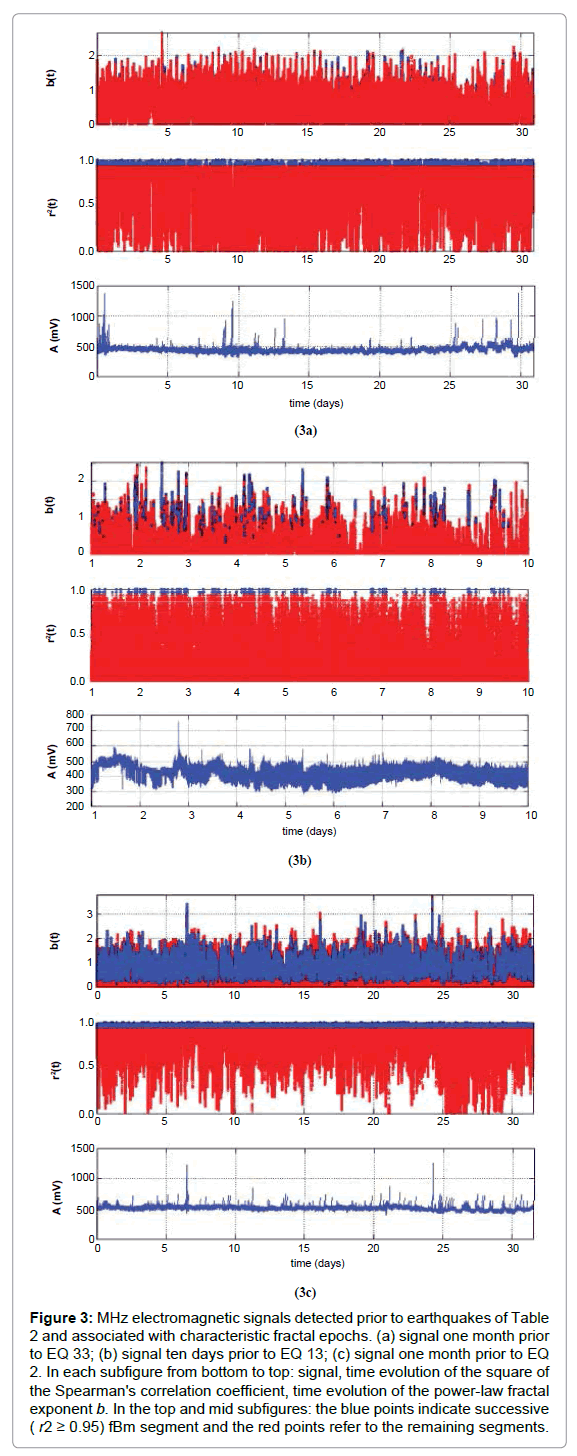
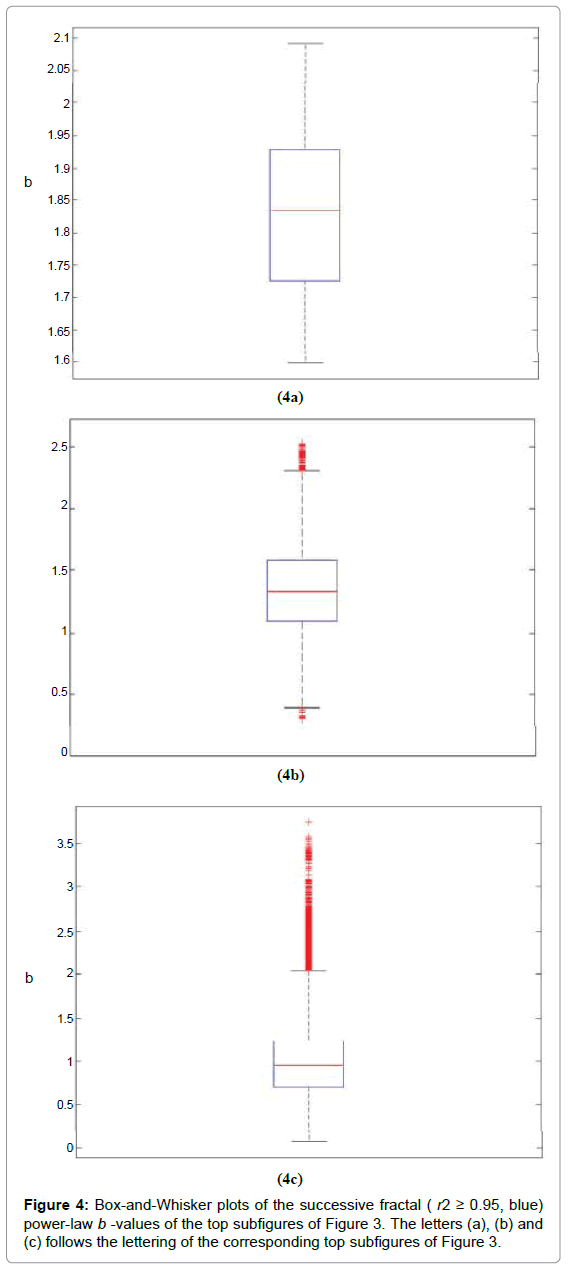
The complex long-term connections between space and time before earthquakes are concealed in traces in earthquake hazard systems [11,16,17,43,44,55-58]. The pre-seismic traces may unfold with fractal methods [3,6,8,9,11,14,16,17,43,44,52,55-58,61,84]. These seismic systems evolve naturally into self-organised critical (SOC) states with fractal organisation in space and time [4]. The evolution of fractals can describe different stages towards the final catastrophe [4,5,8,14,84]. As the SOC states of a seismical system progress and gradually accelerate to the final rupture the system approximates critical points which exhibit long memory trends [8]. These trends can be traced effectively through the identification of temporal power-laws in the power spectral density (PSD) of the associated time series, accounting that the PSD is one of the prevailing measures for that purpose [4,5,8,14,84]. Importantly, when the time-series exhibit noteworthy time-periods of high b - exponent power-laws, they are considered as well-established temporal fractals, which for the cases of the seismical critical systems, are associated with the spatial fractal evolution of the earth's crust during rupture [3,4,6,8,9- 11,14,16-18,43,44,52,55-58,61,84]. In this sense, Figure 3 presents three example cases with the above characteristics, namely time-series containing fractal epochs associated with temporal PSD power-laws close to critical points and associated with long-memory dynamics. Figure 3 was derived by applying the fractal analysis method described in section 2 in three electromagnetic MHz signals collected by the continuous telemetric electromagnetic network of figure 2. Figure 4 shows the corresponding Box-and-Whisker plots of these example cases. What makes important these two associated figures (Figures 3 and 4) is that they enclose and outline different long-memory patterns which require further attention. However, prior to commenting that it is crucial to place emphasis on the following issues as well [e.g.10-13, 16, 17, 43, 44, 55-58, 61, 70, 71, 84 and the referenced therein]: (I) A power-law value of b = 2 means that there is no correlation between the process increments. This means that the disturbance generating system follows random paths driven by non-memory dynamics (randomwalk). (II) The power-law value range 2 < b ≤ 3 suggests the signal’s persistency. This means that the accumulation of the fluctuations of the system is faster than in fBm modelling. (III) The power-law value range 1<b<2 implies anti-persistency. (IV) A power-law value of b = 1 suggests that the fluctuations of the processes do not grow and the electromagnetic signal is stationary. Accounting for these facts, it can be supported that the one-month preseismic signal of Figure 3a (viz. the first example case) exhibits fractal epochs, however, scattered in time. Despite the scattered behaviour of the successive (r2 ≥ 0.95) fractal segments, there can be identified successive fractal segments in this signal with high power-law b - values above 1.5, namely well away from randomness. This can be characteristically observed in Figure 4a. Indeed, all the successive fractal b - values were above 1.6, with the median being almost 1.85. These values are well associated with the fBm class [11,16,17,43,44,55-58] and are considered as pre-earthquake signs of noteworthy value. It is important to note also that some values above 2 can be observed. These are associated with persistency which has been interpreted by some researchers [10-13,70,71] as the most significant precursory sign of the inevitable phase of the earthquake occurrence. According to other researchers [11,16,17,43,44,55-58] the most important sign is the change between anti-persistency and persistency – which can be observed in Figure 3a – whereas the majority of values is well above 1.5 – the case of Figure 4a, as aforementioned. The above arguments hold also for the cases of Figures 3b and 3c. Figure 3b is a ten-day preseismic signal while Figure 3c shows an on month signal. In Figure 3b the variations of the power-law b -values are mild, whereas those of Figure 3c, very intense. When comparing Figures 3a, 3b and 3c, the latter is of increased preseismic value as this exhibits continuous succesive fractal (r2 ≥0.95) behaviour [17] with change between persistency and anti-persistency. It is significant to emphasise that the increased preseismic value is due to the fact that the system generated a self-similar alarm continuously one month prior to this earthquake. However according to Figure 4c, the majority of the successive fractal (r2 ≥ 0.95) epochs were below 1.5 with many of them below 1 ( b <1 ), viz., described by the random fGn class. It is also interesting in Figure 4c, that some outlier values exceeded 3. This peculiar finding has been addressed in preseismic MHz signals [17] as well. The values above 3 correspond to the saturation of the fractal dimension values [17]. On the contrary, the mild variations of the power-law b - values of Figure 3b, despite of higher precursory value [17] in respect to those of Figure 3a at first sight, correspond mainly to b - values between 1 and 1.7 (50% of the cases) which are of lower precursory value when compared to the ones of Figure 4a. It can thus be deduced, that it is of significance to locate characteristic epochs hidden in preseismic time-series in order to trace the inherent long-memory of an earthquake system towards the catastrophe. Accounting for the related fractal-based literature [e.g.10-13, 16, 17, 43, 44, 55-58, 61, 70, 71, 84] and the referenced therein and the aforementioned implications from the results from Figures 3 and 4, it can be supported that, from the fractal-point of view, a pre-earthquake signal of noteworthy precursory value should meet the following criteria: (a) be relatively long; (b) exhibit sufficient number of successive (r2 ≥ 0.95) fBm fractal segments; (c) present low variations in the successive (r2 ≥0.95) segments; (d) the majority of the power-law b - values to be above the threshold of 1.5 and preferably higher, viz., well away from randomness. In this consensus, Table 3 was generated so as to include as many power-law data of the above types as possible. Importantly, Table 3 presents the results of the fractal analysis of all the earthquakes of Table 2, viz., a total of 37 earthquakes. It is very significant to stress the attention to the extent of the analysis of Table 3 since it includes a total of 1819 days of continuous signal days analysed. To the knowledge of the authors of this paper, this is the first approach of this extend, namely with this amount of analysed data and this should be emphasised.
Figure 3: MHz electromagnetic signals detected prior to earthquakes of Table 2 and associated with characteristic fractal epochs. (a) signal one month prior to EQ 33; (b) signal ten days prior to EQ 13; (c) signal one month prior to EQ 2. In each subfigure from bottom to top: signal, time evolution of the square of the Spearman's correlation coefficient, time evolution of the power-law fractal exponent b. In the top and mid subfigures: the blue points indicate successive ( r2 ≥ 0.95) fBm segment and the red points refer to the remaining segments.
| SEISMIC ACTIVITY | Fractal Analysis | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i/i | EQ:n | Location | Lat. (0N) | Long. (0E) | D (km) | L.M.(ML) | f(MHz) | S | T.S.b.V. | Median V.b. | IQR | Min/Max V.b. | %s.V.b.>=1.5 | %s.V.b.>2.0 | |
| 2007 | 1 | 32 | 162.5 km WNW of Florina | 41.46 | 19.68 | 8 | 5 | 41 | J | None | ~ | ~ | ~ | ~ | ~ |
| K | None | ~ | ~ | ~ | ~ | ~ | |||||||||
| 46 | K | Scattered | 0.77 | 0.21 | 0.75/1.46 | 0% | 0% | ||||||||
| 2 | 17 | 19.3 km NNW of Argostoli | 38.34 | 20.42 | 15 | 5.5 | 41 | J | None | ~ | ~ | ~ | ~ | ~ | |
| F | Scattered | 2.15 | 0.25 | 0.80/2.41 | 80% | 73.34% | |||||||||
| 46 | J | None | ~ | ~ | ~ | ~ | ~ | ||||||||
| F | Continuous | 2.31 | 0.2 | 1.20/2.69 | 90% | 75% | |||||||||
| 3 | 33 | 63.8 km SW of Kithira | 35.8 | 22.58 | 99 | 5 | 41 | E | None | ~ | ~ | ~ | ~ | ~ | |
| O | None | ~ | ~ | ~ | ~ | ~ | |||||||||
| V | Scattered | 2.03 | 0.12 | 1.50/2.16 | 100% | 65% | |||||||||
| 46 | V | Scattered | 1.83 | 0.23 | 1.59/2.09 | 100% | 13.34% | ||||||||
| 4 | 28 | 133.6 km WSW of Chania | 34.9 | 22.75 | 34 | 5.1 | 41 | E | None | ~ | ~ | ~ | ~ | ~ | |
| I | Scattered | 1.59 | 1.42 | 0.82/2.00 | 55% | 0% | |||||||||
| 46 | E | None | ~ | ~ | ~ | ~ | ~ | ||||||||
| I | Mild | 2.03 | 0.31 | 0.88/2.21 | 86.67% | 61.54% | |||||||||
| O | None | ~ | ~ | ~ | ~ | ~ | |||||||||
| V | Scattered | 1.84 | 0.24 | 1.21/2.13 | 86.67% | 16.67% | |||||||||
| 2008 | 1 | 3 | 71.1 km SSW of Rodhos | 35.85 | 27.92 | 56 | 6.2 | 41 | V | Continuous | 2.03 | 0.34 | 1.11/2.51 | 96.00% | 0.51 |
| 2 | 16 | 88.2 km S of Methoni | 36.03 | 21.83 | 12 | 5.5 | 41 | V | Continuous | 2.03 | 0.34 | 1.11/2.51 | 96.00% | 0.51 | |
| 46 | V | Mild | 1.48 | 0.51 | 0.69/2.22 | 24% | 3.00% | ||||||||
| 3 | 31 | 99.2 km ESE of Iraklion | 35.11 | 26.19 | 29 | 5 | 41 | V | Continuous | 1.87 | 0.47 | 1.13/2.33 | 85.00% | 0.32 | |
| 4 | 34 | 23.1 km ENE of Andravida | 37.98 | 21.51 | 25 | 6.5 | |||||||||
| 5 | 26 | 39.4 km SSE of Iraklion | 35.01 | 25.33 | 50 | 5.1 | 41 | E | Mild | 2.08 | 0.82 | 1.00/3.37 | 82.59% | 53.34% | |
| V | Continuous | 1.38 | 0.41 | 0.57/2.63 | 37.20% | 0.80% | |||||||||
| 46 | E | Mild | 1.44 | 0.55 | 0.46/2.76 | 36.40% | 11.30% | ||||||||
| V | Continuous | 1.24 | 0.42 | 0.50/2.50 | 23.10% | 1.40% | |||||||||
| 6 | 35 | 34.1 km W of Skyros | 38.92 | 24.17 | 35 | 5 | |||||||||
| 7 | 24 | 95.3 km S of Methoni | 35.96 | 21.7 | 5 | 5.2 | 41 | E | None | ~ | ~ | ~ | ~ | ~ | |
| V | Continuous | 1.26 | 0.4 | 0.25/2.92 | 29.47% | 6.94% | |||||||||
| 46 | E | Scattered | 1.31 | 0.43 | 0.46/2.76 | 30.71% | 3.00% | ||||||||
| V | Continuous | 1.61 | 0.37 | 0.50/2.69 | 64.92% | 7.67% | |||||||||
| 8 | 8 | 70.8 km S of Methoni | 36.18 | 21.72 | 25 | 6 | 41 | E | None | ~ | ~ | ~ | ~ | ~ | |
| V | Continuous | 1.33 | 0.41 | 0.25/2.92 | 28.47% | 7.93% | |||||||||
| 46 | E | Scattered | 1.32 | 0.44 | 0.46/2.76 | 33.17% | 3.50% | ||||||||
| V | Continuous | 1.62 | 0.37 | 0.50/2.69 | 66.82% | 7.18% | |||||||||
| 9 | 27 | 70.0 km S of Methoni | 36.19 | 21.77 | 22 | 5.1 | 41 | E | None | ~ | ~ | ~ | ~ | ~ | |
| V | Continuous | 1.33 | 0.41 | 0.25/2.92 | 28.47% | 7.93% | |||||||||
| 46 | E | Scattered | 1.32 | 0.44 | 0.46/2.76 | 33.17% | 3.50% | ||||||||
| V | Continuous | 1.62 | 0.37 | 0.50/2.69 | 66.82% | 7.18% | |||||||||
| 10 | 6 | 66.5 km S of Methoni | 36.22 | 21.75 | 38 | 6.1 | 41 | E | None | ~ | ~ | ~ | ~ | ~ | |
| V | Continuous | 1.06 | 0.38 | 0.25/2.62 | 23.85% | 2.38% | |||||||||
| 46 | E | Scattered | 1.26 | 0.45 | 0.46/2.22 | 27.20% | 2.20% | ||||||||
| V | Continuous | 1.59 | 0.37 | 0.50/2.69 | 62.22% | 6.33% | |||||||||
| 11 | 4 | 35.9 km SSE of Methoni | 36.5 | 21.78 | 41 | 6.2 | 41 | E | None | ~ | ~ | ~ | ~ | ~ | |
| V | Continuous | 1.06 | 0.38 | 0.25/2.62 | 23.85% | 2.38% | |||||||||
| 46 | E | Scattered | 1.26 | 0.45 | 0.46/2.22 | 27.20% | 2.20% | ||||||||
| V | Continuous | 1.59 | 0.37 | 0.50/2.69 | 62.22% | 6.33% | |||||||||
| 12 | 7 | 9.3 km SW of Leonidhion | 37.11 | 22.78 | 86 | 6.1 | 41 | V | Mild | 0.9 | 0.6 | 0.25/2.56 | 14% | 1.00% | |
| 2009 | 1 | 22 | 51.8 km SW of Zakynthos | 37.47 | 20.47 | 21 | 5.3 | 41 | I | Mild | 1.66 | 0.58 | 0.50/3.00 | 62.55% | 17.06% |
| 46 | I | Mild | 1.57 | 0.54 | 0.50/3.00 | 56.96% | 11.57% | ||||||||
| 2 | 14 | 65.6 km SW of Zakynthos | 37.39 | 20.35 | 39 | 5.6 | 41 | I | Mild | 1.43 | 1.1 | 0.50/3.00 | 46.50% | 14.05% | |
| 3 | 19 | 124.6 km NW of Florina | 41.62 | 20.41 | 10 | 5.4 | 41 | J | Mild | 1.36 | 0.5 | 0.50/2.70 | 34.88% | 2.92% | |
| P | Continuous | 1.6 | 0.52 | 0.50/3.00 | 59,92% | 16.57% | |||||||||
| 46 | J | Continuous | 1.57 | 0.54 | 0.50/3.00 | 56.96% | 11.57% | ||||||||
| P | Continuous | 1.6 | 0.51 | 0.50/3.00 | 60.69% | 15.30% | |||||||||
| 4 | 11 | 111.2 km SSE of Iraklion | 34.35 | 25.4 | 30 | 5.8 | 41 | E | Continuous | 1.43 | 0.49 | 0.50/3.00 | 42.31% | 5.90% | |
| V | Continuous | 1.43 | 0.49 | 0.50/2.95 | 42.31% | 5.90% | |||||||||
| 46 | E | Continuous | 1.48 | 0.6 | 0.50/2.99 | 48.28% | 9.48% | ||||||||
| V | Continuous | 1.35 | 0.55 | 0.50/3.00 | 37.38% | 4.64% | |||||||||
| 5 | 20 | 107.8 km ESE of Karpathos | 35.46 | 28.31 | 42 | 5.4 | 41 | A | Continuous | 1.38 | 0.61 | 0.50/3.00 | 38.41% | 9.90% | |
| 46 | A | Continuous | 1.68 | 0.5 | 0.50/3.00 | 68.20% | 19.41% | ||||||||
| 6 | 25 | 36.0 km NNW of Kilkis | 41.3 | 22.74 | 23 | 5.1 | 41 | T | Continuous | 1.53 | 0.71 | 1.00/3.00 | 52.61% | 21.72% | |
| 46 | T | Continuous | 1.68 | 0.5 | 0.80/3.00 | 61.52% | 16.71% | ||||||||
| 7 | 15 | 74.2 km S of Zakynthos | 37.13 | 20.78 | 15 | 5.5 | 46 | I | Continuous | 1.69 | 0.65 | 0.50/3.00 | 64.51% | 26.48% | |
| 8 | 23 | 68.2 km W of Karpathos | 35.66 | 26.39 | 42 | 5.2 | 41 | E | Mild | 2.21 | 1.29 | 1.00/3.00 | 84.15% | 58.68% | |
| 46 | E | Continuous | 2.81 | 1.41 | 0.50/3.00 | 87.18% | 67.65% | ||||||||
| V | Continuous | 1.49 | 0.53 | 0.50/3.00 | 48.62% | 8.92% | |||||||||
| 9 | 30 | 139.9 km NNW of Florina | 41.94 | 20.74 | 2 | 5 | 41 | J | Continuous | 1.74 | 1.78 | 0.50/3.00 | 62.91% | 39.24% | |
| 46 | J | Continuous | 1.67 | 0.68 | 0.50/3.00 | 57.95% | 25.88% | ||||||||
| 2013 | 1 | 2 | 66.6 km W of Chania | 35.5 | 23.28 | 65 | 6.2 | 41 | A | Mild | 0.98 | 0.6 | 0.40/2.42 | 18.00% | 10.00% |
| 41 | H | Continuous | 1.2 | 0.64 | 0.10/2.80 | 25.03% | 3.14% | ||||||||
| 41 | E | Scattered | 2.04 | 0.74 | 0.50/2.95 | 90.00% | 5.34% | ||||||||
| 41 | V | Continuous | 0.96 | 0.54 | 0.07/3.00 | 11.36% | 1.58% | ||||||||
| 2 | 13 | 116.2 km S of Iraklion | 34.28 | 25.13 | 28 | 5.6 | 41 | E | Mild | 1.32 | 0.48 | 0.50/2.52 | 31.56% | 4.07% | |
| V | Continuous | 1.49 | 0.51 | 0.59/2.82 | 48.27% | 7.61% | |||||||||
| 3 | 10 | 109.7 km S of Iraklion | 34.34 | 25.06 | 32 | 5.8 | 41 | E | Mild | 1.32 | 0.48 | 0.50/2.52 | 31.56% | 4.07% | |
| V | Continuous | 1.49 | 0.51 | 0.50/2.82 | 48.27% | 7.61% | |||||||||
| 2014 | 1 | 36 | 25.6 km NW of Chalkida | 38.64 | 23.41 | 23 | 5.2 | ||||||||
| 2 | 37 | 26.2 km NW of Chalkida | 38.64 | 23.4 | 24 | 5.2 | |||||||||
| 3 | 12 | 69.4 km W of Milos | 36.67 | 23.67 | 97 | 5.7 | 41 | E | Scattered | 0.72 | 0.19 | 038/1.35 | 0.00% | 0.00% | |
| 46 | E | Scattered | 0.86 | 0.41 | 0.25/1.62 | 1.16% | 0.00% | ||||||||
| V | Scattered | 0.82 | 0.2 | 0.26/1.77 | 0.70% | 0.00% | |||||||||
| 4 | 29 | 50.6 km S of Poliyiros | 39.92 | 23.46 | 29 | 5 | 41 | J | Scattered | 0.76 | 0.2 | 0.28/1.58 | 0.10% | 0.00% | |
| K | Continuous | ~ | ~ | ~ | 0.8/1.6 | ~ | |||||||||
| 46 | J | Mild | ~ | ~ | ~ | 0.8/1.7 | ~ | ||||||||
| T | Continuous | ~ | ~ | ~ | 0.2/2.2 | ~ | |||||||||
| 5 | 1 | 22.9 km SSW of Samothraki | 40.29 | 25.4 | 28 | 6.3 | 41 | M | Continuous | 0.73 | 0.25 | 0.30/1.94 | 4.60% | 0.00% | |
| T | Mild | 0.77 | 0.34 | 0.03/2.02 | 1.63% | 0.07% | |||||||||
| 46 | M | Scattered | 1.06 | 0.33 | 0.89/1.35 | 0,00% | 0.00% | ||||||||
| T | Continuous | 1.04 | 0.6 | 0.05/2.09 | 15.07% | 0.03% | |||||||||
| 6 | 9 | 6.7 km NE of Argostoli | 38.22 | 20.53 | 21 | 5.8 | 41 | F | Scattered | 2.1 | 0.2 | 0.80/2.40 | 80% | 73.34% | |
| 2015 | 1 | 18 | 67.2 km SSW of Karpathos | 35.16 | 26.74 | 40 | 5.4 | 46 | E | Continuous | ~ | ~ | 0.3/1.8 | ~ | ~ |
| 2 | 5 | 56.7 km SSW of Karpathos | 35.23 | 26.82 | 37 | 6.1 | 46 | E | Continuous | ~ | ~ | 0.3/1.8 | ~ | ~ | |
| 3 | 21 | 52.9 km W of Karpathos | 35.68 | 26.56 | 67 | 5.3 | 46 | E | Continuous | ~ | ~ | 0.3/1.8 | ~ | ~ | |
Table 3: Collection of the results derived through the spectral fractal analysis. The purple rows refer to the radon precursors. The remaining rows refer to the MHz precursors. Columns 1-3: Different colouring for each year. Columns 9 and 10: Different colouring for each MHz channel (except of the radon precursors). ~ is employed for no data (please see text as well). EQ:n is the number of each earthquake in Table 2.
Very significant is to note that the shallow earthquake EQ:19 (Table 3) produced also a continuous one-month fractal pre-seismic warning in the Corfu station. In comparison, the same earthquake (EQ:19, Table 3) did not give a continuous alarm of such type to the near Ioannina station but rather a scattered alarm. Probably, this could be an indication of the sensitivity or the locality of each station regarding the collection of MHz pre-seismic signals. Locality and sensitivity are considered a common issue of the ULF network stations [1,2]. Important is to mention that there were no systematic observations both in the 41 MHz and the 46 MHz frequencies of the temporal power-law b - profiles of the aforementioned type, even from the data of the same earthquake and from the same station. The systematics of the observations indicate that it is a fortunate conjuncture to recognise: (1) simultaneous visual anomalies in the recordings of a certain station in both the 41 MHz and the 46 MHz frequencies, (2) in parallel with high power-law b -values.
In Table 3, the epicentre locations of Table 2 are repeated in order to illustrate the distance between the epicentre and the station's MHz time-series that were employed in the fractal analysis. The following abbreviations were used in Table 3: (1) (S): Station Letter. For reference the reader could see and Figure 2. (2) (L.M.): Local Magnitude of the earthquake. This was derived from the data of the National Observatory of Athens. (3) (f): Frequency of the antennas for the cases of the MHz electromagnetic radiation. Purple was employed for the 46 MHz and grey for the 41 MHz. (4) (Lat.): Latitude of the epicentre of the earthquake. (5) (Long.): Longitude of the epicentre of the earthquake. (6) (D): Depth of the epicentre of the earthquake. (7) (T.S.b.V.): Typification of successful b - values. This refers to a quality quantification of the images of the time evolution of the successive power-law b - values. The quality quantification was arbitrarily characterised as scattered, mild and continuous in the manner used above in text (Figure 3). (8) (Median Vb): Median value of the evolution of b - values. This value corresponds to the threshold value, above which the 50% of b - values are. The Median Vb was calculated after the end of each run from the output ASCII file which contained the full b - data. This was an output of the custom made software generated for that purpose. (9) (IQR): Interquartile range of b - values. It corresponds to the difference between the upper (3rd) and lower (1st) quartiles, viz., IQR = Q3-Q1. Q1 corresponds to the cut-off value, below of which 25% of the b-values are. Q3 corresponds to the threshold value above which the 75% of of the b-values are. IQR contains, more or less, the 50% of b - values. IQR was calculated after the end of each run, as in (9), from the ASCII file which contained the full b - data. This was an output of the custom made software. (10) (Min/Max V.b): Minimum/Maximum value of b. (11) %Vb >=1.5: The percentage of values above 1.5. As aforementioned, this value was selected as a threshold value adequate to discriminate between long-memory critical dynamics and randomness (please see also text). (12) %Vb >=2.0: The percentage of values above 2.0. This value was selected by other investigators as another value adequate to discriminate long-memory dynamics from randomness (please see also text). The missing values in Table 3 were due to deficient computer runs, namely cases where the ASCII file of the full b - data was not produced. It should be stressed here that the corresponding fractal analysis of all the electromagnetic and radon data of Table 3 took approximately 1300 days to implement and for this reason it was selected not to repeat the deficient runs only to additionally generate the b - data ASCII file. This justifies the missing data. In the sense of the above argumentation and according to the opinion of the authors, the data of Table 3 imply that a noteworthy pre-earthquake sign is not simply to identify some power-law b - values above a threshold as for example in [10,11], but rather the combination of the following issues: (I) The T.S.b.V. to be continuous, namely to observe continuously high b -values (above a threshold) during a certain period. To the opinion of the authors, this discriminates strongly the long-memory dynamics from randomness. (II) The median value Vb to be high, because this indicates that the great majority of b-values are high; and this is a good sign for a pre-earthquake activity.(III) %Vb>1.5 and %Vb>2 to be high. In the sense of the above argumentation (I-II), as well as, according to the data presented in text, several cases of noteworthy precursory value can be identified in Table 3. Characteristic such examples are the following specific data of Table 3: (1) EQ:17, 41 and 46 MHz, station F. (2) EQ:3 and EQ: 16, 41 MHz, station V. (3) EQ:24, 41 MHz and 46 MHz, station V. (4) EQ:27, 46 MHz, station V. (5) EQ:4, 46 MHz, station V. (6) EQs: 19, 20, 25, 15. (7) EQ:34 and EQ:35 identified through radon. It is important to emphasise in Table 3, that there were detected deep undersea earthquakes which gave continuous alarms, as for example EQ:11 41 MHz and 46 MHz, stations E and V and EQ:10 41 MHz station V. It is worth to mention that these MHz pre-earthquake signals were, more or less, detected and exhibited noteworthy fractal behaviour, despite that the focal points and depths of the corresponding earthquakes prohibit, in principle, the transferability of the MHz electromagnetic waves. It is, possibly, the complicated transport of micro-cracks [8-11,14,16,17,43,44,55-58], and the extent of the heterogeneous medium that obstructs the crackslip [8-11], which could provide air pathways to earth’s surface for the MHz radiation.
According to the aspects expressed so-far and the findings of Figures 3 and Table 3 the MHz radiation and the variations of the radon-in soil show several precursory signs of significant value. The various fractal regimes that were detected imply that the corresponding signals exhibited long-range spatial-temporal correlations, i.e., strong memory of the system which generated the electromagnetic or the radon disturbances. This significant implication means that each value of the time-series within these key-periods/regimes, correlates not only to its most recent value but also to its long-term history in a scale-invariant, fractal manner [9-11,16,17,27,43]. Hence, the history of the system defines its future (non-Markovian behaviour) [9-11,16,17,27,43]. This suggests that the underlying dynamics are governed by positive feedback mechanisms and, thus, any external influences tend to lead the system out of equilibrium [85]. The system acquires, hence, a selfregulating character and, to a great extent, the property of irreversibility, one of the important components of prediction reliability [86]. From another viewpoint, this behaviour suggests that the final output of fracture is affected by many processes that act on different time scales [3,4,9]. All these results are in good agreement with a hypothesis that the evolution of the earth’s crust towards general failure takes place as a SOC phenomenon [9-11,16,17,27,43]. All these issues are compatible with the last stages of the generation of earthquake. Observing the data of Table 3, it can be observed that the Hellenic network showed sensitivity differentiations due to locality. For example, all earthquakes of 2009 with M L ≥ 5.0 were pre-signalised through interrupted or continuous MHz fractal segments of long memory. Two earthquakes were detected by two more stations. The remaining stations did not give MHz signals with characteristic pre-earthquake fractal footprints. Data, although of great amount, are still limited to identify the sensitivity dependencies of the Hellenic network. It can be observed also that there are some significant pre-signalised earthquakes gave fractal warnings up to one month prior to some events. Some warnings evolved up to some hours prior to the earthquake. The remaining investigated MHz signals gave significant alarms 2-3 weeks and 1 week prior to the event. The latter is the most usual behaviour (Table 3). It may be supported hence that the MHz electromagnetic and the radon precursors correspond to the same pre-earthquake phase. The time lag of the radon precursors can be up to 2-3 months prior to the event. Although several associations were reported, the available data are based only on the fractal analysis is still limited, so as to attempt an association of the dependence of the earthquake data with the station that identified a pre-seismic sign, as well as a further investigation of the role of the earthquake parameters, namely depth and position of the epicentre. What complicates the situation is that the fractal methods are not sufficient to signalise that an earthquake is going to occur in some near or far area. Such results should be combined with other long-memory methods or methods of self-organisation, in order to provide better estimations [e.g. 55, 58]. Even in such a case, it is still questionable, whether a certain earthquake can, up-to-now, be associated to an anomaly of some kind.
Conclusions
Summarising the most important findings, the following issues can be supported:
1. Thirty-three pre-seismic MHz electromagnetic disturbances lasting between some days up to one-month duration and four lengthy radon variations recorded prior to earthquakes of 2007, 2008, 2009, 2014, 2015 with M L ≥ 5.0, indicated that the MHz electromagnetic, as well as, the radon disturbances can be used as reliable pre-seismic precursors of noteworthy scientific value.
2. Almost all the investigated signals (both MHz and radon) exhibited characteristic epochs with fractal organisation in space and time. Continuous epochs were detected in several MHz one-month signals.
3. The precursor fractal epochs were considered those with successive (r2 ≥ 0.95) power-law behaviour with the corresponding power-law b - exponent in the fBm class (1 ≤ b ≤ 3).
4. Enhanced precursory fractal epochs were considered the successive fBm ones with many successive (r2 ≥ 0.95) segments above 1.5 and better, above 2.0. These epochs indicated wellestablished long-memory dynamics well away from fGn randomness.
5. Several successive (r2 ≥ 0.95) fractal electromagnetic and radon segments showed anti-persistency (1.5 < b < 2.0). Numerous persistent (2.0 < b < 3.0) parts were also detected. Although several references suggested that the MHz electromagnetic precursors show only anti-persistent behaviour, the systematics of this research supported a different aspect, namely the change between anti-persistency and persistency. The switching between anti-persistency and persistency enhances the precursory value of the electromagnetic and radon precursors.
6. The Hellenic electromagnetic network showed sensitivity differentiations due to locality. For example, all earthquakes of 2009 with M L ≥ 5.0 were pre-signalised through interrupted or continuous fractal segments of long memory. Two earthquakes were detected by two more stations. The remaining stations did not give MHz signals with characteristic pre-earthquake fractal footprints. The results, although of great amount, are still limited to identify the sensitivity dependencies of the Hellenic network.
7. Significant pre-signalised earthquakes gave fractal warnings up to one month prior to some events. Some warnings evolved up to some hours prior to the earthquake. The remaining investigated MHz signals gave significant alarms 2-3 weeks and 1 week prior to the event. The latter is the most usual behaviour (Table 3). It may be supported hence that the MHz electromagnetic and the radon precursors correspond to the same pre-earthquake phase. It may be also supported that the MHz electromagnetic provides pre-seismic signs ranging from some weeks up to some hours prior to the event. The time lag of the radon precursors can be up to 2-3 months prior to the event.
8. The findings indicate self-organised critical state characteristics of the last stages of the investigated earthquakes.
9. The fractal analysis method can be employed as a first screening method for the identification of long-memory patterns hidden in pre-seismic time-series. It is also, from the results, a reliable method for identifying pre-earthquake patterns.
References
- Varotsos P, Alexopoulos K (1984) Physical properties of the variations of the electric field of the earth preceding earthquakes. I Tectonophysics 110: 73-98.
- Varotsos P, Alexopoulos K (1984) Physical properties of the variations of the electric field of the earth preceding earthquakes, II, determination of epicenter and magnitude. Tectonophysics 110: 99-125.
- Smirnova N, Hayakawa M, Gotoh K (2004) Precursory behaviour of fractal characteristics of the ULF electromagnetic fields in seismic active zones before strong earthquakes. Phys Chem Earth 29: 445-451.
- Smirnova, N, Hayakawa M (2007) Fractal characteristics of the ground-observed ULF emissions in relation to geomagnetic and seismic activities. J Atmos Sol-Terr Phys 69: 1833-1841.
- Hayakawa M, Hobara Y (2010) Current status of seismo-electromagnetics for short-term earthquake prediction. Geomat Nat Haz Risk 1:115-155.
- Eftaxias K (2010) Footprints of non-extensive Tsallis statistics, self-affinity and universality in the preparation of the L'Aquila earthquake hidden in a pre-seismic EM emission. Physic A 389: 133-140.
- Varotsos PA, Sarlis NV, Skordas ES (2011) Scale-specific order parameter fluctuations of seismicity in natural time before main shocks. EPL 96: 59002-p1/59002-p6.
- Kapiris P, Eftaxias K, Nomikos K, Polygiannakis J, Dologlou E, et al. (2003) Evolving towards a critical point: A possible electromagnetic way in which the critical regime is reached as the rupture approaches. Nonlinear Process Geophys. 10: 511-524.
- Eftaxias K, Contoyiannis Y, Balasis G, Karamanos K, Kopanas J, et al. (2008) Evidence of fractional-Brownian-motion-type asperity model for earthquake generation in candidate pre-seismic electromagnetic emissions. NHESS 8: 657-669.
- Eftaxias K, Athanasopoulou L, Balasis G, Kalimeri M, Nikolopoulos S, et al. (2009) Unfolding the procedure of characterizing recorded ultra low frequency, kHz and MHz electromagnetic anomalies prior to the L’Aquila earthquake as pre-seismic ones – Part 1. NHESS 9: 1953-1971.
- Eftaxias K, Balasis G, Contoyiannis Y, Papadimitriou C, Kalimeri M, et al. (2010) Unfolding the procedure of characterizing recorded ultra low frequency, kHZ and MHz electromagnetic anomalies prior to the L’Aquila earthquake as pre-seismic ones - Part 2. NHESS 10: 275-294
- Minadakis G, Potirakis S, Nomicos C, Eftaxias K (2012) Linking electromagnetic precursors with earthquake dynamics: An approach based on non-extensive fragment and self-affine asperity models. Physica A 391: 2232-2244.
- Potirakis S, Minadakis G, Eftaxias K (2012) Analysis of electromagnetic pre-seismic emissions using Fisher information and Tsallis entropy. Physica A 391: 300-306.
- Kapiris P, Polygiannakis J, Peratzakis A, Nomicos K, Eftaxias K (2002) VHF-electromagnetic evidence of the underlying pre-seismic critical stage. Earth Planets Space 54: 1237-1246.
- Stavrakas I, Clarke M, Koulouras G, Stavrakakis G, Nomicos C (2007) Study of directivity effect on electromagnetic emissions in the HF band as earthquake precursors: Preliminary results on field observations. Tectonophysics 431: 263-271.
- Petraki E, Nikolopoulos D, Fotopoulos A, Panagiotaras D, Koulouras G, et al. (2013) Self-organised critical features in soil radon and MHz electromagnetic disturbances: Results from environmental monitoring in Greece. Appl Radiat Isot 72: 39-53.
- Petraki E, Nikolopoulos D, Chaldeos Y, Coulouras G, Nomicos C, et al. (2016) Fractal evolution of MHz electromagnetic signals prior to earthquakes: results collected in Greece during 2009. Geomat Nat Haz Risk 7: 550-564.
- Yonaiguchi N, Ida Y, Hayakawa M, Masuda S (2007) Fractal analysis for VHF electromagnetic noises and the identification of preseismic signature of an earthquake. J Atmos Sol-Terr Phys 69: 1825-1832.
- Kalimeri M, Papadimitriou C, Balasis G, Eftaxias K (2008) Dynamical complexity detection in pre-seismic emissions using non-additive Tsallis entrop. Physica A 387: 1161-1172.
- Eftaxias K, Panin V, Deryugin Y (2007) Evolution-EM signals before earthquakes in terms of meso-mechanics and complexity. Tectonophysics 431: 273-300.
- Cicerone R, Ebel J, Britton J (2009) A systematic compilation of earthquake precursors. Tectonophysics 476: 371-396.
- Nazaroff W, Nero A (1988) Radon and its decay products in indoor air. Wiley, New York.
- Vogiannis E, Nikolopoulos D (2015) Radon sources and associated risk in terms of exposure and dose. Front Pub Heal Env Heal 2: 207.
- Nikolopoulos D, Louizi A (2008) Study of indoor radon and radon in drinking water in Greece and Cyprus: implications to exposure and dose. Rad Meas 43: 1305-1314.
- Ghosh D, Deb A, Sengupta R (2009) Anomalous radon emission as precursor of earthquake. J App Geophys 69: 67-81.
- Khayrat AH, Oliver MA, Durrani SA (2001) The effect of soil particle size on soil radon concentration. Rad Meas 34: 365-371.
- Nikolopoulos D, Petraki E, Marousaki A, Potirakis S, Koulouras G, et al. (2012) Environmental monitoring of radon in soil during a very seismically active period occurred in South West Greece. J Environ Monitor 14: 564-578.
- Richon P, Bernard P, Labed V, Sabroux J, Beneito A, et al (2007) Results of monitoring 222Rn in soil gas of the Gulf of Corinth region, Greece. Rad Meas 42: 87-93.
- Whitehead NE, Barry BJ, Ditchburn RG, Morris CJ, Stewart MK (2007) Systematics of radon at the Wairakei geothermal region, New Zealand. J Env Rad 92: 16-29.
- Vogiannis E, Nikolopoulos D (2008) Modelling of radon concentration peaks in thermal spas: Application to Polichnitos and Eftalou spas (Lesvos Island-Greece). Sc Tot Env 405: 36-44.
- Al-Tamimi MH, Abumura KM (2001) Radon anomalies along faults in North of Jordan. Rad Meas 34: 397-400.
- King CY (1985) Impulsive radon emanation on a creeping segment of the San Andreas fault, California. Pure App Geophys 122: 340-352.
- King CY (1980) Episodic radon changes in Subsurface soil gas along active faults and possible relation to earthquakes. J Geophys Res 85: 3065-3078
- Tansi C, Tallarico A, Iovine G, Gallo MF, Falcone G (2005) Interpretation of radon anomalies in seismotectonic and tectonic-gravitational settings: the south-eastern Crati graben (Northern Calabria, Italy). Tectonophys 396: 181-193.
- Walia V, Yang T, Hong W, Lin S, Fu C, et al. (2009) Geochemical variation of soil–gas composition for fault trace and earthquake precursory studies along the Hsincheng fault in NW Taiwan. App Rad Isot 67: 1855-1863.
- Zafrir H, Steinitz G, Malik U, Haquin G, Gazit-Yaari N (2009) Response of Radon in a seismic calibration explosion, Israel. Rad Meas 44: 193-198.
- Imme´ G, Delf SL, Nigro SL, Morelli D, Patane´ G (2005) Gas radon emission related to geodynamic activity on Mt. Etna. Ann Geophys 48: 65-71.
- Morelli D, Martino SD, Imme´ G, Delfa SL, Nigro SL, et al. (2006) Evidence of soil radon as tracer of magma uprising in Mt. Etna. Rad Meas 41: 721-725.
- Chyi L, Quick T, Yang T, Chen C (2005) Soil gas radon spectra and earthquakes. Ter Atmc Oc Sci 4: 763-774.
- Ghosh D, Deb A, Dutta S, Sengupta R (2012) Multifractality of radon concentration variation in earthquake related signal. Fractals 20: 33-39.
- Kuo T, Lin C, Fan K, Chang G, Lewis C, et al. (2009) Radon anomalies precursory to the 2003 Mw = 6.8 Chengkung and 2006 Mw = 6.1 Taitung earthquakes in Taiwan. Radiation Measurements 44: 295-299.
- Majumdar K (2004) A study of fluctuation in radon concentration behaviour as an earthquake precursor. Curr Sci 86: 1288-1292.
- Nikolopoulos D, Petraki E, Vogiannis E, Chaldeos Y, Giannakopoulos P, et al. (2014) Traces of self-organisation and long-range memory in variations of environmental radon in soil: Comparative results from monitoring in Lesvos Island and Ileia (Greece). J Radioanal Nucl Chem 299: 203-219.
- Petraki E, Nikolopoulos D, Fotopoulos A, Panagiotaras D, Nomicos C, et al. (2013) Long-range memory patterns in variations of environmental radon in soil. Anal Methods 5: 4010-4020.
- Singh M, Ramola R, Singh B, Singh S, Virk H (1991) Subsurface soil gas radon changes associated with earthquakes. Nuc Trac Rad Meas 19: 417-420.
- Singh S, Kumar A, Singh BB, Mahajan S, Kumar V, et al. (2010) Radon Monitoring in Soil Gas and Ground Water for Earthquake Prediction Studies in North West Himalayas, India. Terr Atm Oc Sci 21: 685-695.
- Dieker T (2004) Simulation of fractional Brownian motion (Thesis dissertation). Amsterdam: University of Twente, Department of Mathematical Sciences.
- Yannakoloulos PH (2012) Digital Communications. Athens, Greece: Sinchroni Ekdotiki E.P.E.
- Wornell G (1995) Signal Processing with Fractals. A wavelet-based approach. Indianapolis, United States of America: BooksCraft, Inc.
- Hurst H (1951) Long Term Storage Capacity of Reservoirs. T Am Soc Civ Eng 116: 770-799.
- Mandelbrot BB, Van Ness JW (1968) Fractional Brownian motions, fractional noises and applications. SIAM Rev Soc Ind Appl Math 10: 422-437.
- Petraki E, Nikolopoulos D, Nomicos C, Stonham J, Cantzos D, et al. (2015) Electromagnetic Pre-earthquake Precursors: Mechanisms, Data and Models-A Review. J Earth Sci Clim Change 6: 1-11.
- Shrivastava A (2014) Are pre-seismic ULF electromagnetic emissions considered as a reliable diagnostics for earthquake prediction? Curr Sci 107: 596-600.
- Uyeda S, Nagao T, Kamogawa M (2009) Short-term earthquake prediction: current status of seismo-electromagnetics. Tectonophys 470: 205-213.
- Cantzos D, Nikolopoulos D, Petraki E, Nomicos C, Yannakopoulos PH, et al. (2015) Identifying Long-Memory Trends in Pre-Seismic MHz Disturbances through Support Vector Machines. J Earth Sci Clim Change 6: 1-9.
- Nikolopoulos D, Petraki E, Nomicos C, Koulouras G, Kottou S, et al. (2015) Long-Memory Trends in Disturbances of Radon in Soil Prior ML=5.1 Earthquakes of 17 November 2014 Greece. J Earth Sci Clim Change 6: 1-11.
- Nikolopoulos D, Cantzos D, Petraki E, Yannakopoulos PH, Nomicos CD (2016) Traces of long-memory in pre-seismic MHz electromagnetic time series-Part1: Investigation through the R/S analysis and time-evolving spectral fractals. J Earth Sci Clim Change (in press).
- Cantzos D, Nikolopoulos D, Petraki E, Yannakopoulos PH, Nomicos CD (2016) Fractal analysis, information-theoretic similarities and SVM classification for multichannel, multi-frequency pre-seismic electromagnetic measurements. J Earth Sci Clim Change 7: 1-9.
- Fraser-Smith AC, Bernardi A, McGill PR, Ladd ME, Helliwell RA, Viilard OG (1990). Low-frequency magnetic field measurements near the epicenter of the Ms 7.1 Loma Prieta earthquake. Geophys Res Lett 17: 1465-1468.
- Fujinawa Y, Takahashi K (1998) Electromagnetic radiations associated with major earthquakes. Phys Earth Planet Inter 105: 249-259.
- Hayakawa M, Ida Y, Gotoh K (2005) Multifractal analysis for the ULF geomagnetic data during the Guam earthquake. Electromagnetic Compatibility and Electromagnetic Ecology, 2005. IEEE 6th International Symposium 2005: 239-243.
- Kopytenko Yu A, Matiashviali TG, Voronov PM, Kopytenko EA, Molchanov OA (1993) Detection of ultra-low-frequency emissions connected with the Spitak earthquake and its aftershock activity, based on geomagnetic pulsations data at Dusheti and Vardzia observatories. Phys Earth Planet Inter 77: 85-95.
- Smith B, Johnston M (1976) A tectonomagnetic effect observed before a magnitude 5.2 earthquake near Hollister, California. J Geophys Res 81: 3556-3560.
- Eftaxias K, Kapiris P, Polygiannakis J, Bogris N, Kopanas J, et al. (2001) Signature of pending earthquake from electromagnetic anomalies. Geophys Res Lett 29: 3321-3324.
- Eftaxias K, Kapiris P, Dologlou E, Kopanas J, Bogris N, et al. (2002) EM anomalies before the Kozani earthquake: a study of their behavior through laboratory experiments. Geophys Res Lett 29: 1-4.
- Enomoto Y, Tsutsumi A, Fujinawa Y, Kasahara M, Hashimoto H (1997) Candidate precursors: pulse-like geoelectric signals possibly related to recent seismic activity in Japan. Geophys J Int 131: 485-494.
- Maeda K, Tokimasa N (1996) Decametric radiation at the time of the Hyogo-ken Nanbu earthquake near Kobe in 1995. Geophys Res Lett 23: 2433-2436.
- Varotsos P, Sarlis N, Eftaxias K, Lazaridou M, Bogris N, et al. (1999) Prediction of the 6.6 Grevena-Kozani Earthquake of May 13, 1995. Phys Chem Earth 24: 115-121.
- Warwick J, Stoker C, Meyer T (1982) Radio Emission Associated With Rock Fracture: Possible Application to the Great Chilean Earthquake of May 22, 1960. J Geophys Res 87: 2851-2859.
- Potirakis SM, Minadakis G, Eftaxias K (2013) Relation between seismicity and pre-earthquake electromagnetic emissions in terms of energy, information and entropy content. NHESS 12: 1179-1183.
- Potirakis SM, Minadakis G, Nomicos C, Eftaxias K (2011) A multidisciplinary analysis for traces of the last state of earthquake generation in preseismic electromagnetic emissions. NHESS 11: 2859-2879.
- Thomas D (1988) Geochemical precursors to seismic activity. Pure Appl Geophys 126: 241-266.
- Namvaran M, Negarestani A (2012) Measuring the radon concentration and investigating the mechanism of decline prior to earthquake. J Radioanal Nucl Chem 298: 1-8.
- King CY (1985) Impulsive radon emanation on a creeping segment of the San Andreas fault, California. Pure Appl Geophys 122: 340-352.
- Chyi LL, Quick TJ, Yang TF, Chen CH (2010) The experimental investigation of soil gas radon migration mechanisms and its implication in earthquake forecast. GEOFLUIDS 10: 556-563.
- Chyi LL, Quick TJ, Yang TF, Chen CH (2011) The origin and detection of spike-like anomalies in soil gas radon time series. Geochem J 45: 431-438.
- Sac MM, Harmansah C, Camgoz B, Sozbilir H (2011) Radon Monitoring as the Earthquake precursor in Fault Line in Western Turkey. Ecology 20: 93-98.
- Zoran M, Savastru R, Savastru D, Chitaru C, Baschir L, et al. (2012) Monitoring of radon anomalies in South-Eastern part of Romania for earthquake surveillance. J Radioanal Nucl Chem 293:769-781.
- Choubey VM, Kumar N, Arora BR (2009) Precursory signatures in the radon and geohydrological borehole data for M4.9 Kharsali earthquake of Garhwal Himalaya. Sci Total Environ 407: 5877-5883.
- Nomicos K, Vallianatos F (1998) Electromagnetic variations associated with the seismicity of the frontal Hellenic arc. Geol Carpath 49: 57-60.
- Koulouras G, Kontakos K, Stavrakas I, Stonham J, Nomicos K (2005) Embedded Compact Flash. IEEE Circuits Devices Mag 21: 27-34.
- Genitron V (1997) Alpha Guard PQ2000/MC50 Multiparameter Radon Monitor Germany, Frankfurt: Genitron Instruments.
- Roumelioti Z, Benetatos C, Kiratzi A (2009) The 14 February 2008 earthquake (M6.7) sequence offshore south Peloponnese (Greece): source models of the three strongest events. Tectonophysics 471: 272-284.
- Surkov V, Uyeda S, Tanaka H, Hayakawa M (2002) Fractal properties of medium and seismoelectric phenomena. J Geodyn 33: 477-487.
- Telesca L, Lasaponara R (2006) Vegetational patterns in burned and unburned areas investigated by using the detrended fluctuation analysis. Physica A 368: 531-535.
- Morgounov V (2001) Relaxation creep model of impending earthquake. Ann Geophys 44: 369-381.
Relevant Topics
- Atmosphere
- Atmospheric Chemistry
- Atmospheric inversions
- Biosphere
- Chemical Oceanography
- Climate Modeling
- Crystallography
- Disaster Science
- Earth Science
- Ecology
- Environmental Degradation
- Gemology
- Geochemistry
- Geochronology
- Geomicrobiology
- Geomorphology
- Geosciences
- Geostatistics
- Glaciology
- Microplastic Pollution
- Mineralogy
- Soil Erosion and Land Degradation
Recommended Journals
Article Tools
Article Usage
- Total views: 4619
- [From(publication date):
November-2016 - Aug 28, 2025] - Breakdown by view type
- HTML page views : 3576
- PDF downloads : 1043