Multicollinearity in Regression Analyses Conducted in Epidemiologic Studies
Received: 15-Feb-2016 / Accepted Date: 29-Feb-2016 / Published Date: 07-Mar-2016 DOI: 10.4172/2161-1165.1000227
Abstract
The adverse impact of ignoring multicollinearity on findings and data interpretation in regression analysis is very well documented in the statistical literature. The failure to identify and report multicollinearity could result in misleading interpretations of the results. A review of epidemiological literature in PubMed from January 2004 to December 2013, illustrated the need for a greater attention to identifying and minimizing the effect of multicollinearity in analysis of data from epidemiologic studies. We used simulated datasets and real life data from the Cameron County Hispanic Cohort to demonstrate the adverse effects of multicollinearity in the regression analysis and encourage researchers to consider the diagnostic for multicollinearity as one of the steps in regression analysis.
Keywords: Multicollinearity; Regression analysis; Simulation; BMI; Waist circumference
164138Introduction
Multicollinearity arises when at least two highly correlated predictors are assessed simultaneously in a regression model. The adverse impact of multicollinearity in regression analysis is very well recognized and much attention to its effect is documented in the literature [1-11]. The statistical literature emphasizes that the main problem associated with multicollinearity includes unstable and biased standard errors leading to very unstable p-values for assessing the statistical significance of predictors, which could result in unrealistic and untenable interpretations [4,7,12,13]. Multicollinearity does not affect the overall fit or the predictions of the model [14]. If the purpose of the regression model is to investigate associations, multicollinearity among the predictor variables can obscure the computation and identification of key independent effects of collinear predictor variables on the outcome variable because of the overlapping information they share. When the predictor variables are highly correlated the common interpretation of a regression coefficient of one predictor as measuring the change in expected value of the response variable due to one unit increase in that predictor variable when holding the other predictors constant may be practically impossible [14]. These can lead to misleading conclusions for the role of each of the collinear predictors in the regression model. For example, using multivariable logistic regression to analyze data from a nested case-control study revealed that some carotenoids were inversely associated with breast cancer suggesting that plasma levels of α- or β-carotene may play a role in reducing breast cancer risk [15]. The authors reported that they had limited ability to conclude whether the observed association is specific for α-carotene due to a high degree of collinearity between the plasma carotenoids. As another example, in order to develop efficient public health interventions addressing the obesity epidemic, Leal et al. [16] had a methodological challenge to disentangle the effects of highly correlated neighborhood characteristics and identify exactly which aspects of the environments (physical and service) influence obesity risk. Individual/neighborhood socioeconomic adjusted physical and service-related neighborhood characteristics were inversely associated with BMI/waist circumference, but the authors reported that they were unable to determine which one of these factors had an independent effect on BMI/waist circumference [16].
Although conducting a multicollinearity diagnosis does not solve nor lead to any specific solution of the problem, realizing its potential impact on findings from regression analysis allows a more careful interpretation of data. For example, when the purpose of a multivariable regression analysis is to explain the individual effects of the predictors on an outcome variable, it is important that a potential multicollinearity between the predictors be investigated; a potential severity be quantified; and potential impact of multicollinearity on the reported results are acknowledged and discussed. A recent non-systematic review of epidemiological papers listed in PubMed for the period from January 2004 to December 2013 by our research team, revealed that in a majority of epidemiologic studies that performed regression analysis the diagnostic for identifying potential multicollinearity are not performed. For example, to investigate the role of the intrauterine environment in childhood adiposity, Fleten et al. (2012) [17] considered multivariable linear regression analyses of children’s body mass index (BMI) as an outcome on several prenatal and postnatal factors, including both parental BMIs [17]. The authors noted decrease in both parentaloffspring associations of BMI after adjusting for other factors, but the largest decrease in coefficient estimate for a parent’s BMI occurred after adjusting for the other parent’s BMI. The parents’ BMI are expected to be highly correlated, but no multicollinearity diagnostic was performed to investigate and discuss the potential impact of multicollinearity in the instability of the estimated coefficients when BMIs from both parents were kept in the regression model. Numerous studies [18-22] have shown that BMIs of spouses are correlated possibly due to the shared environment and the change in the coefficient estimate may be due to collinearity between the BMIs of spouses. Similarly, Desai et al. [23] investigated independent effects of selected variables on diastolic dysfunction as an outcome variable, defined as severe-diastolic dysfunction versus normal diastolic function, using polytomous logistic regression analysis [23]. Some of the predictors were BMI, waist circumference (WC), triglycerides, total cholesterol, high density lipoprotein (HDL), blood glucose, systolic and diastolic blood pressure. Multicollinearity diagnostic among the predictors was not discussed despite evidence in the literature that significant positive correlation among BMI, age, systolic and diastolic blood pressure may exist [24]. On the other hand, BMI and WC are some of the widely known risk factors for obesity related health outcomes and some studies [25,26] reported significant correlation between these two variables that may cause multicollinearity when both of these variables are included simultaneously in a regression model. Janssen et al. [27] investigated whether BMI and WC have independent effects on obesity–related health risks using a logistic regression model when adjusting for age, gender, smoking, alcohol intake, and poverty ratio [27]. Although, after adjusting for confounding variables, WC and BMI individually were strong predictors of co-morbidities, when both of these variables were included in the model, BMI was no longer a significant predictor. No multicollinearity diagnostic was reported in the paper and its potential impact on the findings were discussed [27]. Similarly, Feller et al. (2010) [26] examined how the risk for type 2 diabetes can be explained by BMI and WC. The authors used Cox proportional hazard regression model and assessed both variables together including their interaction term. The authors reported a high correlation between these variables, but they did not conduct multicollinearity diagnostic to determine whether reported results for inverse relationship between BMI and diabetes in women, or non-significant regression coefficient for BMI, were due to multicollinearity [26].
In order to assess the magnitude of this problem in clinical and epidemiological studies we estimated the frequency of not performing multicollinearity diagnostic in regression analyses by conducting a non-systematic search in PubMed for the period from January 2004 to December 2013. Because of the difference between the terms multivariable or multiple regression and the term multivariate regressions [28] we restricted the search only to multivariable and multiple regressions, which are often used interchangeably in epidemiologic literature. Next, among papers using the terms multivariable regression, multiple regression or regression, we searched for terms collinearity, multicollinearity, collinear or multicollinear. The search result revealed that in PubMed the terms collinearity, multicollinearity, collinear or multicollinear were found in only 0.12% of the studies that used multivariable regression. Although these percentages are subject to limitations as whether the papers searched had issues related to multicollinearity, it is clear that a majority of these papers did not acknowledge and did not discuss the impact of multicollinearity on the their findings.
The main aim of this study was to demonstrate the effect of different degrees of multicollinearity among predictors on their regression coefficients and the corresponding standard errors estimates as well as the potential impact on the p-values using generated simulated datasets with different scenarios for multicollinearity between the predictors. Since multicollinearity in a regression can involve more than two independent variables, in this simulation study we considered three independent variables with varying pairwise Pearson product moment correlation coefficients. Furthermore, using data from the Cameron County Hispanic Cohort (CCHC), we demonstrated the effect of multicollinearity caused by Body Mass Index (BMI) and waist circumference (WC) on two outcome variables a) systolic blood pressure and b) diastolic blood pressure in two separate linear regression analyses.
Materials and Methods
Simulation study for investigating the effect of multicollinearity on regression parameters
Dataset Generation
Several datasets of sample size 800 with one response variable y and three predictors xi , i=1, 2, 3 were generated from a multivariate normal distributions MVN 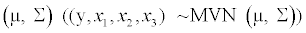 with mean vector
with mean vector 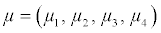 =(116.68, 30.98, 101.7, 45.14) that resemble the distributions of systolic blood pressure, BMI, waist circumference and age observed in CCHC data. For the purpose of these simulations, we considered a4×4 covariance matrix Σ=DRD where R is a pre-specified correlation matrix define in Table 1 and D is a diagonal matrix with elements on the diagonal representing the standard deviations
=(116.68, 30.98, 101.7, 45.14) that resemble the distributions of systolic blood pressure, BMI, waist circumference and age observed in CCHC data. For the purpose of these simulations, we considered a4×4 covariance matrix Σ=DRD where R is a pre-specified correlation matrix define in Table 1 and D is a diagonal matrix with elements on the diagonal representing the standard deviations 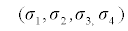 = (17.32,6.73,15.35,15.42) of the observed variables systolic blood pressure, BMI, waist circumference and age, respectively. The Covariance matrix Σ was calculated using the formula
= (17.32,6.73,15.35,15.42) of the observed variables systolic blood pressure, BMI, waist circumference and age, respectively. The Covariance matrix Σ was calculated using the formula 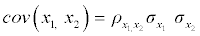 where ρ x1,x2 is correlation of two random variables x1 and x2;σ x1 and σ x2 are the standard deviations of x1 and x2, respectively.
where ρ x1,x2 is correlation of two random variables x1 and x2;σ x1 and σ x2 are the standard deviations of x1 and x2, respectively.
| Correlation Scenario | Corr(y, x1) | Corr(y, x2) | Corr(y, x3) | Corr(x1, x2) | Corr (x2, x3) | Corr(x1, x3) |
|---|---|---|---|---|---|---|
| 1 | 0.17 | 0.2 | 0.43 | 0.1 | 0.1 | 0.1 |
| 2 | 0.17 | 0.2 | 0.43 | 0.25 | 0.1 | 0.1 |
| 3 | 0.17 | 0.2 | 0.43 | 0.5 | 0.1 | 0.1 |
| 4 | 0.17 | 0.2 | 0.43 | 0.85 | 0.1 | 0.1 |
| 5 | 0.17 | 0.2 | 0.43 | 0.25 | 0.25 | 0.1 |
| 6 | 0.17 | 0.2 | 0.43 | 0.5 | 0.25 | 0.1 |
| 7 | 0.17 | 0.2 | 0.43 | 0.85 | 0.25 | 0.1 |
| 8 | 0.17 | 0.2 | 0.43 | 0.85 | 0.5 | 0.1 |
| 9 | 0.17 | 0.2 | 0.43 | 0.25 | 0.25 | 0.25 |
| 10 | 0.17 | 0.2 | 0.43 | 0.5 | 0.5 | 0.5 |
| 11 | 0.17 | 0.2 | 0.43 | 0.85 | 0.5 | 0.25 |
| 12 | 0.17 | 0.2 | 0.43 | 0.85 | 0.85 | 0.5 |
Table 1: Correlation matrices R considered in simulating datasets with variables y, x1, x2, and x3 with different degrees of collinearity.
Since the signs of the correlation coefficients between predictors and the correlations between the response variable and the predictors can moderate the effect of the collinearity on parameter inference [12], for the purpose of this simulation study, all pairwise correlation coefficients were positive and the correlations between the response variable y and the predictors xi, i=1,2,3 were fixed and estimated based on data from the CCHC, as shown in Table 1. To simulate predictor variables with different degree of collinearity, the Pearson pairwise correlation coefficients were varied from a weak correlation (i.e.,0<= |r|< 0.3) to a moderate correlation (i.e., 0.3≤|r|<0.7) and a strong correlation (i.e., |r|>=7). As shown in Table 1, different degrees of correlation coefficients were considered between x1 and x2 only, both independent of x3.The generated datasets were replicated 1000 times.
Model Comparisons
Various multivariable linear regression models (1) using least squares approach were fitted under each of the scenarios representing the correlation matrix and dataset replications using the generated datasets with response variable y and predictors x1, x2, and x3:
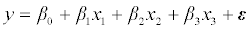 ……………………..(1)
……………………..(1)
where β0, β1, β2, and β3 are the regression coefficients and the error term ε is normally distributed with mean 0 and variance 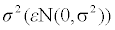
Multicollinearity was assessed using variance inflation factor (VIF) [14], which measures the inflation in the variances of the parameter estimates due to multicollinearity potentially caused by the correlated predictors. In each scenario for correlation matrix the average estimates of regression coefficient, standard errors, t-test statistics, p-values, and VIF over the 1000 simulations were calculated.
To illustrate the effects of different degrees of multicollinearity on regression estimates, the estimated regression coefficients, their standard errors, t-test statistics, p-values and VIFs of the models with the larger pairwise correlation coefficients between the predictor variables x1, x2, and x3 were compared to the those of the model with the smallest pairwise correlation coefficients between x1, x2, and x3 in scenario 1.
On the other hand, to demonstrate how the coefficient estimates, their standard errors, t-test statistics, ρ-values and VIF change when adding a variable in the model with different degrees of correlation with other variables in the model we fit the multivariable linear regression model.
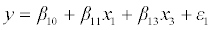 ……………..(2)
……………..(2)
Where β10, β11, and β13 are the regression coefficients and the error term ε1 is normally distributed with mean 0 and variance σ1 2 and model
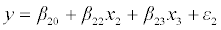 ………………..(3)
………………..(3)
Where β20, β22, and β23 are the corresponding regression coefficients and the error term ε2 is normally distributed with mean 0 and variance σ2 2. The averaged parameter estimates for variables x1 and x2 from models (2) and (3) are then compared to the corresponding estimates from model (1). For simplicity, these comparisons were performed only under correlation scenarios 1, 2, 3 and 4 where the correlation between x1 and x2 increased from 0.1 to 0.85, while the correlation coefficients between x1 and x3, x2 and x3 were held fixed at 0.1.
Empirical example for multicollinearity based on the analysis of Cameron County Hispanic Cohort data
To demonstrate the effect of multicollinearity between predictors in regression models in real life epidemiologic studies, in this section we present the analyses of empirical data from Cameron County Hispanic Cohort (CCHC) using linear regression models. The study population is the Brownsville population represented by CCHC initiated in Cameron County, Texas in 2004, and currently includes more than 3000 participants of age 18 years or older. Information regarding sampling and eligibility criteria of the cohort participants and data collection has been reported previously [29].
The response variables of interest were baseline systolic blood pressure and diastolic blood pressure as continuous variables. Readings of blood pressure were taken following standard protocols. Participants sat quietly for 5 minutes and then readings were taken three times 5 minutes apart using a Hawksley Random Zero sphygmomanometer. Diastolic blood pressure was determined at the 5th Korotkoff sound. The final pressure was based on the average of the 2nd and 3rd measurements.
The predictors of interest were Body mass index (BMI) and waist circumference (WC), known to be highly correlated obesity related risk factors. Other covariates, such as age at initial visit (baseline), family history of hypertension, smoking and drinking status, as well as education were included in the regression analysis. Waist circumference (visceral adiposity) was measured at the level of the umbilicus to the nearest 10th cm, with the participant in a standing position and breathing normally. Height was measured to the nearest 10th cm using a stadiometer. Weight (to the nearest 10th kilogram) was measured on a calibrated beam balance. BMI was calculated as weight in kilograms divided by height squared in meters (kg/m2).
The Committee for the Protection of Human Subjects at the University of Texas Health Science Center at Houston approved the study protocol, written consent forms and procedures and free and informed consent was obtained from all subjects. The investigators had no conflict of interest to disclose at consent.
Data Analysis
Three linear regression models for each of the predictors systolic and diastolic blood pressure were fitted using least squares approach: (1) models with BMI and waist circumference individually and (2) a model including both predictors BMI and waist circumference, all controlled for the effect of age, gender, smoking and drinking status, family history of hypertension and education level. Multicollinearity between BMI and waist circumference was assessed using VIF [14]. In order to investigate the potential effect of multicollinearity, based on the results from the simulation study, we estimated the regression coefficients and their corresponding standard errors and p-values of BMI and waist circumference when both variables were included in model (2), which was compared to the corresponding regression parameters estimates from using model (1).
All simulations and statistical analyses were performed using SAS 9.4 [30]. All statistical tests were two-sided and were performed at 5% level of significance.
Results
Simulation study
Table 2 provides the averaged estimates of regression coefficient, standard errors, t-test statistics, p-values and VIF over the 1000 simulations under each correlation scenario. The comparisons, measured in percent change, of estimates from models with higher degree of multicollinearity to estimates from the model with the lowest degree of multicollinearity in scenario 1.
| Correlation Scenario (Corr(x1, x2), Corr(x2, x3), Corr(x1, x3)) | Predictor Variable | Parameter Estimate | Standard Error | t Value | Pr> |t| | VIF | %Change Coefficient Estimate based on scenario 1* | % Change in Standard Error based on scenario 1* | % Change in t Value based on scenario 1* | % Change in Variance Inflationbased on scenario 1* |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 (.1,.1,.1) | Intercept | 70.08 | 4.34 | 16.18 | <.0001 | 0 | 0 | 0 | 0 | 0 |
| x1 | 0.3 | 0.08 | 3.65 | 0.0101 | 1.02 | 0 | 0 | 0 | 0 | |
| x 2 | 0.17 | 0.04 | 4.68 | 0.0008 | 1.02 | 0 | 0 | 0 | 0 | |
| x 3 | 0.45 | 0.04 | 12.86 | <.0001 | 1.02 | 0 | 0 | 0 | 0 | |
| 2 (.25,.1,.1) | Intercept | 72.93 | 4.14 | 17.63 | <.0001 | 0 | 4.07 | -4.5 | 8.96 | 0 |
| x1 | 0.24 | 0.08 | 2.9 | 0.0382 | 1.08 | -18.14 | 2.91 | -20.55 | 5.33 | |
| x 2 | 0.15 | 0.04 | 4.21 | 0.0038 | 1.08 | -7.53 | 2.78 | -10.04 | 5.36 | |
| x 3 | 0.46 | 0.04 | 12.91 | <.0001 | 1.02 | 0.4 | 0.03 | 0.39 | -0.24 | |
| 3 (.5,.1,.1) | Intercept | 76.11 | 3.93 | 19.4 | <.0001 | 0 | 8.6 | -9.4 | 19.9 | 0 |
| x1 | 0.17 | 0.09 | 1.86 | 0.1746 | 1.34 | -41.05 | 15.47 | -49.04 | 31.39 | |
| x 2 | 0.14 | 0.04 | 3.46 | 0.0122 | 1.34 | -14.77 | 15.29 | -26.07 | 31.34 | |
| x 3 | 0.46 | 0.04 | 12.95 | <.0001 | 1.02 | 1.15 | 0.42 | 0.7 | -0.53 | |
| 4 (.85,.1,.1) | Intercept | 77.08 | 4.02 | 19.21 | <.0001 | 0 | 9.98 | -7.35 | 18.73 | 0 |
| x1 | -0.05 | 0.15 | -0.34 | 0.495 | 3.64 | -117.73 | 90.15 | -109.32 | 255.94 | |
| x 2 | 0.2 | 0.07 | 2.93 | 0.0359 | 3.63 | 18.98 | 89.94 | -37.39 | 255.9 | |
| x 3 | 0.47 | 0.04 | 13.14 | <.0001 | 1.01 | 2.75 | 0.59 | 2.18 | -0.76 | |
| 5 (.25,.25,.1) | Intercept | 78.92 | 4.07 | 19.43 | <.0001 | 0 | 12.61 | -6.18 | 20.09 | 0 |
| x1 | 0.29 | 0.08 | 3.48 | 0.015 | 1.07 | -1.58 | 3.34 | -4.66 | 4.96 | |
| x 2 | 0.08 | 0.04 | 2.2 | 0.1138 | 1.13 | -50.2 | 6.18 | -52.99 | 10.84 | |
| x 3 | 0.45 | 0.04 | 12.33 | <.0001 | 1.07 | -0.71 | 3.56 | -4.12 | 4.92 | |
| 6 (.5,.25,.1) | Intercept | 82.52 | 3.83 | 21.56 | <.0001 | 0 | 17.74 | -11.65 | 33.25 | 0 |
| x1 | 0.28 | 0.09 | 2.95 | 0.0344 | 1.34 | -6.47 | 15.79 | -19.18 | 30.91 | |
| x 2 | 0.05 | 0.04 | 1.13 | 0.3327 | 1.41 | -71.44 | 18.88 | -75.85 | 38.33 | |
| x 3 | 0.46 | 0.04 | 12.55 | <.0001 | 1.07 | 1.22 | 3.76 | -2.41 | 4.85 | |
| 7 (.85,.25,.1) | Intercept | 87.48 | 3.86 | 22.71 | <.0001 | 0 | 24.82 | -11.06 | 40.36 | 0 |
| x1 | 0.44 | 0.16 | 2.77 | 0.0455 | 3.81 | 48.63 | 95.62 | -24.11 | 272.72 | |
| x 2 | -0.06 | 0.07 | -0.82 | 0.4069 | 4.02 | -135.02 | 100.7 | -117.52 | 293.64 | |
| x 3 | 0.48 | 0.04 | 12.68 | <.0001 | 1.12 | 5.06 | 6.56 | -1.4 | 10.08 | |
| 8 (.85,.5,.1) | Intercept | 118.26 | 3.74 | 31.68 | <.0001 | 0 | 68.75 | -13.8 | 95.8 | 0 |
| x1 | 2.69 | 0.2 | 13.39 | <.0001 | 7.33 | 811.49 | 148.21 | 266.85 | 617.85 | |
| x 2 | -1.28 | 0.1 | -12.63 | <.0001 | 9.69 | -869.35 | 185.11 | -369.87 | 849.21 | |
| x 3 | 1 | 0.05 | 18.74 | <.0001 | 2.72 | 120.24 | 51.14 | 45.72 | 166.13 | |
| 9 (.25,.25,.25) | Intercept | 82.52 | 4.06 | 20.33 | <.0001 | 0 | 17.74 | -6.3 | 25.65 | 0 |
| x1 | 0.13 | 0.09 | 1.46 | 0.268 | 1.12 | -57.38 | 6.33 | -60 | 9.17 | |
| x 2 | 0.1 | 0.04 | 2.66 | 0.0594 | 1.11 | -39.75 | 6.01 | -43.16 | 9.12 | |
| x 3 | 0.44 | 0.04 | 11.84 | <.0001 | 1.12 | -2.19 | 6.27 | -7.93 | 9.25 | |
| 10 (.5,.5,.5) | Intercept | 97.9 | 3.84 | 25.5 | <.0001 | 0 | 39.69 | -11.35 | 57.6 | 0 |
| x1 | -0.15 | 0.1 | -1.49 | 0.249 | 1.5 | -150.83 | 24.42 | -140.82 | 47.34 | |
| x 2 | 0 | 0.04 | 0.03 | 0.5073 | 1.5 | -99.09 | 24.25 | -99.36 | 47.31 | |
| x 3 | 0.51 | 0.04 | 11.7 | <.0001 | 1.5 | 13.19 | 24.39 | -9.02 | 47.3 | |
| 11 (.85,.5,.25) | Intercept | 103.2 | 3.88 | 26.66 | <.0001 | 0 | 47.25 | -10.61 | 64.77 | 0 |
| x1 | 0.85 | 0.17 | 5.08 | 0.0003 | 4.23 | 186.15 | 105.48 | 39.18 | 314.32 | |
| x 2 | -0.38 | 0.08 | -4.69 | 0.0006 | 5.29 | -330.12 | 129.47 | -200.21 | 417.93 | |
| x 3 | 0.58 | 0.04 | 13.15 | <.0001 | 1.57 | 27.93 | 25.09 | 2.26 | 53.45 | |
| 12 (.85,.85,.85) | Intercept | 254 | 4.27 | 59.59 | <.0001 | 0 | 262.43 | -1.59 | 268.29 | 0 |
| x1 | 5.41 | 0.15 | 35.53 | <.0001 | 10.1 | 1731.77 | 88.07 | 873.42 | 890.17 | |
| x 2 | -4.31 | 0.11 | -39.22 | <.0001 | 27.4 | -2688.58 | 208.88 | -938.03 | 2578.29 | |
| x 3 | 2.95 | 0.07 | 44.27 | <.0001 | 10.1 | 548.07 | 88.25 | 244.25 | 891.6 |
Table 2: Results from multivariable linear regression models fitted using simulated data under different scenarios for pairwise correlations between the predictors. *Comparison of estimates of models with higher degree of multicollinearity to estimates of the model with the lowest degree of multicollinearity in scenario 1.
Scenarios with two correlated predictors: In correlation matrix scenarios 1, 2, 3 and 4 the correlation between x1 and x2 increased from 0.1 to 0.85, while the correlations between x1 and x3, x2 and x3 were held fixed at 0.1. Larger change as well as a switch in the sign and the statistical significance of the regression coefficient estimates was observed for one of the variables x1 involved in the multicollinearity when the correlation between x1 and x2 was 0.5 and 0.85. In the last two cases VIF for variable x1 was 1.34 and 3.64, respectively.
Scenarios with three correlated predictors: In correlation matrix scenarios 5, 6, and 7 variable x2 had a weak to moderate correlation with variable x3 (r=0.25), and at the same time variable x2 had a varying correlation from 0.1 to 0.85 with variable x1, while the correlation between x1 and x3 were held fixed at 0.1. As the correlation between the two variables x1 and x2 increased, the results showed changes in estimates and values of test statistics for all variables when compared to the model in scenario 1. Larger changes were observed for variables x1 and x2, in particular for variable x2, which altered the statistical significance of the regression coefficient estimates when the correlation between x1 and x2 became 0.25, and altered its sign when the correlation between x1 and x2 was 0.85. Similar were the results in correlation scenario 8 when the correlation between x2 and x3 was increased to 0.5.
Interesting were the results in correlation scenarios 5, 9 and 10. In the correlation scenario 5 the correlation in two pairs was set to 0.25 and in the correlation scenario 9 the pairwise correlation between all three variables was set to 0.25. Larger changes in regression coefficient estimates, standard errors, values of test statistics, and switch in the statistical significance to non-significance were observed for two of the predictors (x1 and x2), while the change in VIF was only 9% (from VIF=1.02 to VIF=1.12). The results were similar to correlation scenario 10 where the pairwise correlation between all three variables was set to 0.5. The only difference was that with the increase of the pairwise correlation between all variables from 0.25 (scenario 9) to 0.5, regression coefficient estimate of one of the variables (x2) changed its sign.
Finally, in the last two scenarios the correlation between x1 and x2 was set to 0.85. All variables were involved in multicollinearity of different degrees by varying the pairwise correlations between x1 and x3 and x2 and x3 from 0.25 to 0.85. The percent change in the coefficient estimates, standard errors, values of test statistics and VIF was very large and switching in signs was observed for coefficient estimate of variable x2.
Table 3 presents how the coefficient estimates, their standard errors, values of test statistics, p-values and VIF changed when adding variable x1 (or x2) in the model with variable x2 (or x1) and x3, and the correlation between x1 and x2 increased from 0.1 to 0.85, while the correlations between x1 and x3 (Model (2)), x2 and x3 (Model (3)) was fixed at 0.1. Models (2) and (3), respectively, with two predictors with fixed correlation resulted in identical regression coefficients and corresponding standard errors estimates across the four correlations scenarios. When variable x2, was added to model (2) with predictors x1 and x3 and the correlation between x1 and x2 was 0.5 and 0.85 increasing in standard error estimates (12.5% and 87.5%), decrease in the magnitude of the regression coefficient estimates (-48.5% and -115.2%), and switching in the sign and the statistical significance was observed for variable. In contrast, the inclusion of variable x2 in model (2) with predictors x1 and x3 when the correlation between x1 and x2 was 0.1 or 0.25 did not impact as high the magnitude of the regression coefficient estimates of variable x_1 (9.1% and 27.3%); its standard error remained unchanged (0.0% and 0.0%) and therefore it did not alter its significance.
| Models | Model (2) | Model (3) | Model (1) | Model (2) compared to Model (1) | Model (3) compared toModel (1) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Correlation Scenario (Corr(x1, x2), Corr(x2, x3), Corr(x1, x3)) | Variable | Parameter Estimate | SE | Pr> |t| | VIF | Parameter Estimate | SE | Pr> |t| | VIF | Parameter Estimate | SE | Pr> |t| | VIF | %Change in Parameter Estimates | %Change in SE | %Change in Parameter Estimates | %Change in SE |
| 1 (.1,.1,.1) | Intercept | 85.24 | 2.92 | <.0001 | 0 | 77.5 | 3.86 | <.0001 | 0 | 70.08 | 4.34 | <.0001 | 0 | -17.79 | 48.63 | -9.57 | 12.44 |
| x1 | 0.33 | 0.08 | 0.005 | 1 | 0.3 | 0.08 | 0.01 | 1 | -9.09 | 0 | |||||||
| x 2 | 0.18 | 0.04 | 4.00E-04 | 1 | 0.17 | 0.04 | 8.00E-04 | 1 | -5.56 | 0 | |||||||
| x 3 | 0.47 | 0.04 | <.0001 | 1 | 0.47 | 0.04 | <.0001 | 1 | 0.45 | 0.04 | <.0001 | 1 | -4.26 | 0 | -4.26 | 0 | |
| 2 (.25,.1,.1) | Intercept | 85.42 | 2.92 | <.0001 | 0 | 77.45 | 3.85 | <.0001 | 0 | 72.93 | 4.14 | <.0001 | 0 | -14.62 | 41.78 | -5.84 | 7.53 |
| x1 | 0.33 | 0.08 | 0.005 | 1 | 0.24 | 0.08 | 0.038 | 1.1 | -27.27 | 0 | |||||||
| x 2 | 0.18 | 0.04 | 6.00E-04 | 1 | 0.15 | 0.04 | 0.004 | 1.1 | -16.67 | 0 | |||||||
| x 3 | 0.47 | 0.04 | <.0001 | 1 | 0.46 | 0.04 | <.0001 | 1 | 0.46 | 0.04 | <.0001 | 1 | -2.13 | 0 | 0 | 0 | |
| 3 (.5,.1,.1) | Intercept | 85.27 | 2.92 | <.0001 | 0 | 77.48 | 3.86 | <.0001 | 0 | 76.11 | 3.93 | <.0001 | 0 | -10.74 | 34.59 | -1.77 | 1.81 |
| x1 | 0.33 | 0.08 | 0.004 | 1 | 0.17 | 0.09 | 0.175 | 1.3 | -48.48 | 12.5 | |||||||
| x 2 | 0.18 | 0.04 | 1.00E-04 | 1 | 0.14 | 0.04 | 0.012 | 1.3 | -22.22 | 0 | |||||||
| x 3 | 0.47 | 0.04 | <.0001 | 1 | 0.46 | 0.04 | <.0001 | 1 | 0.46 | 0.04 | <.0001 | 1 | -2.13 | 0 | 0 | 0 | |
| 4(.85,.1,.1) | Intercept | 85.21 | 2.92 | <.0001 | 0 | 77.46 | 3.86 | <.0001 | 0 | 77.08 | 4.02 | <.0001 | 0 | -9.54 | 37.67 | -0.49 | 4.15 |
| x1 | 0.33 | 0.08 | 0.004 | 1 | -0.05 | 0.15 | 0.495 | 3.6 | -115.15 | 87.5 | |||||||
| x 2 | 0.18 | 0.04 | 3.00E-04 | 1 | 0.2 | 0.07 | 0.036 | 3.6 | 11.11 | 75 | |||||||
| x 3 | 0.47 | 0.04 | <.0001 | 1 | 0.47 | 0.04 | <.0001 | 1 | 0.47 | 0.04 | <.0001 | 1 | 0 | 0 | 0 | 0 | |
Table 3: Comparison of estimates between multivariable linear regressions nested models fitted using simulated data under scenarios from 1 to 4 for pairwise correlation between the predictors.
Results from the analysis of CCHC data
BMI and WC were highly correlated with correlation coefficient of 0.86 (p-value<0.0001). The correlation coefficients between BMI and WC and the rest of the covariates included in the models were less than 0.2. Table 4 presents the results from multivariable linear regression models of systolic and diastolic blood pressure on BMI (model 1), waist circumference (model 2) and BMI and waist circumference (model 3) when covariates age, gender, smoking and drinking status, family history of hypertension and education level were added of these models. When BMI and waist circumference were assessed individually, they were significantly associated with systolic blood pressure, controlling for the other covariates. When both variables BMI and waist circumference were assessed together in a model, BMI was still significantly associated with systolic blood pressure (p-value<0.0001) but the association of waist circumference with systolic blood pressure was no longer significant (p-value=0.0526). The changes in BMI coefficient estimate and its standard error in the last model were 33% and 125%, respectively; and for waist circumference -162% and 100%, respectively. In addition, when BMI and waist circumference were assessed in separate models, while other covariates kept in the model, their VIFs were 1.01 and 1.06, respectively. When BMI and waist circumference were assessed together, while other covariates kept in the model, their VIFs increased to 4.48 and 4.46, respectively, indicating potential for multicollinearity.
| Variables | Estimates | Models* for Systolic Blood Pressure | Models* for Diastolic Blood Pressure | ||||
|---|---|---|---|---|---|---|---|
| Model 1† | Model 2‡ | Model 3^ | Model 1† | Model 2‡ | Model 3^ | ||
| BMI | Coefficient estimate | 0.4 | 0.53 | 0.34 | 0.43 | ||
| SE | 0.04 | 0.09 | 0.03 | 0.06 | |||
| p-value | <0.0001 | <0.0001 | <0.0001 | <0.0001 | |||
| VIF | 1.01 | 4.48 | 1.01 | 4.48 | |||
| Waist circumference | Coefficient estimate | 0.13 | -0.08 | 0.12 | -0.05 | ||
| SE | 0.02 | 0.04 | 0.01 | 0.03 | |||
| p-value | <0.0001 | 0.0526 | <0.0001 | 0.0679 | |||
| VIF | 1.06 | 4.67 | 1.06 | 4.67 | |||
Table 4: Results from multivariable linear regression models of systolic and diastolic blood pressure fitted using Cameron County Hispanic Cohort data, 2003-2014.
Similar results were observed in the models for diastolic blood pressure when the effects of BMI and waist circumference assessed individually or both in the model simultaneously. When assessed individually, BMI and waist circumference were significantly associated with diastolic blood pressure (both p-values<0.0001), controlling for the other covariates. When both variables BMI and waist circumference were included together in a model and controlled for the other covariates., BMI was still significantly associated with diastolic blood pressure (p-value<0.0001), but the association between waist circumference and diastolic blood pressure was no longer significant (p-value=0.0679). In the models with BMI and WC, coefficient estimate for BMI increased by at least 30% and the standard error of coefficient estimate for BMI increased by more than 100%. Changes were observed in the coefficient estimate and its standard error for WC, by more than 140% and a reduction of 100%, respectively. VIF of BMI and waist circumference in the three models changed as well. When BMI and waist circumference were assessed in separate models, while controlling for the other covariates, their VIFs were 1.01 and 1.06, respectively. When BMI and waist circumference were included together in a model, while controlling for the other covariates, their VIFs changed to 4.48 and 4.46, respectively.
Discussion
Using simulated data we demonstrated how different degrees of multicollinearity between independent variables in multivariable regression models affect the parameter estimates of the collinear variables in the model and their standard errors. According to the Gauss- Markov Theorem if all the underlying assumptions of the regression models are met (e.g., correctly specified with no assumptions violated), then the least square regression coefficient estimates are unbiased and have minimum variance among all unbiased linear estimators [14]. This is true even in the presence of high collinearity between the regression predictors as long as they are estimable. Although the parameter estimates are unbiased in the correctly specified model (1) in all different correlation scenarios, the comparisons across scenarios showed that even small increase in the pairwise correlation from 0.1 (correlation scenario 1) to 0.25 (correlation scenario 2) caused changes in the magnitude of the regression coefficient estimates and their standard errors for the collinear variables. The magnitude of the changes in the regression slopes estimates and their variances were related to the degree of collinearity between the predictors in the model. Mathematically, the regression coefficient estimates and their variances can be expressed as functions of the correlations of each predictor with all of the other predictors [14,31]. The greater the correlation between the predictors in the model the greater the change in the slopes estimates and their standard errors.
When only two of the predictors in model (1) were correlated with correlation coefficient of 0.5 and there were no other correlations among the predictors in the models the statistical significance of one of the correlated variables diminished due to the change in regression coefficient and standard error estimate. The variables involved in this multicollinearity had VIFs of 1.34. When the correlation between the same variables increased to 0.85 (e.g., highly positively correlated) the regression coefficient of the same correlated variable changed its sign from positive to negative (e.g., the regression coefficient estimates of the correlated variable had opposite signs). The variables involved in this multicollinearity had VIFs of 3.64 and 3.63, respectively.
Further, we demonstrated how multicollinearity involved more than two variables with weak pairwise correlation coefficients and impacted the coefficient estimates and their standard errors. Reduction in the statistical significance was observed when more than two predictors in the model had the pairwise correlation increased to 0.25. VIF for the variable that changed the statistical significance was 1.13.
We compared the estimates from a model with two predictors with pairwise correlation of 0.1 to the corresponding estimates from the models after adding a third variable with different degrees of correlation with one of the variables already in the model. Based on the current simulation study the models with two predictors were miss-specified models and the models with three predictors were the correctly specified models. In this case the changes in the regression estimates and their standard errors when adding a third variable in the model were result of adding an incorrectly omitted variable in the model. However, increase in changes in the regression slope and its standard error were only observed for the predictor with the increased degree of pairwise correlation from 0.1 to 0.85 with the added variable in the model, controlling for the other covariates. The change in the slope for the second variable in the model with two predictors, which had a very small pairwise correlation of 0.1 with the added predictor, was smaller and no change in the standard error was observed.
Using CCHC data we found that, when assessed individually in two separate linear regression models, the two highly correlated variables BMI and waist circumference were significantly an directly associated with systolic and diastolic blood pressure after controlling for age, gender, smoking and drinking status, family history of hypertension and education level. Given that the correlation between BMI and WC was very high (r=0.86), we expected a significant impact on magnitude and direction of regression parameter estimates and their standard errors. This effect was observed when analyzing data from the CCHC study when both variables BMI and WC were assessed together. Specifically, when evaluated together, only BMI was significantly associated with systolic and diastolic blood pressure, while the estimate of WC coefficient was no longer significant and with a negative coefficient. Similar effect was also demonstrated with the simulation studies when a third predictor was added to the model with two predictors. In reality the researcher does not know what the true model is and larger changes in slope estimates and variances when adding (or removing) a variable in a model may indicate a potential for multicollinearity. Lastly, the indication for potential multicollineaity issue - the VIFs for BMI and WC increased from 1.01 and 1.08 to 4.48 and 4.67, respectively, when evaluated together in a regression model.
Since this study focused on recognition of multicollinearity in regression analysis, in this paper we do not fully discus the findings from the CCHC data. The results from the individual analysis of BMI and WC were in agreement with the direction of results reported from other studies that increased BMI and WC were associated with elevated blood pressure [32-34]. When BMI and WC were entered together in a linear regression model for systolic and diastolic blood pressure, WC was no longer significantly associated with systolic and diastolic blood pressure. Similarly, in another study conducted by Song et al. (2014) [35] only BMI was associated with blood pressure and high blood pressure when evaluated together with WC in a logistic regression [35].
Multicollinearity diagnostic
When a multicollinearity diagnostic is considered, pairwise correlation coefficients between predictors and VIF are the most common tools for inspection used by statisticians and epidemiologists. Some investigators use correlation coefficients cutoffs of 0.5 and above [36] but most typical cutoff is 0.80 [37]. Although VIF of greater than 5 or VIF greater than 10 [14] are suggested for detecting multicollinearity, there is no universal agreement as what the cut-off based on values of VIF should be used to detect multicollinearity. Our study demonstrated that even VIF<5 could impact the results from an epidemiologic study. Caution for misdiagnosis of multicollinearity using low pairwise correlation and low VIF was reported in the literature for collinearity diagnostic as well [37-39]. O’Brien (2007) [8] demonstrated that VIF rules of thumb should be interpreted with cautions and should be put in context of the effects of other factors that influence the stability of the specific regression coefficient estimate [8,40] and suggested that any VIF cut-off value should be based on practical consideration. Freund et al. [40] also suggested VIF to be evaluated against the overall fit of the model, using the model R2 statistics. VIF>1/(1-overall model R2) indicates that correlation between the predictors is stronger than the regression relationship and multicollinearity can affect their coefficient estimates [40]. Other commonly used multicollinearity diagnostic measures are the condition number (CN), sometimes called condition index (CI) assisted by the regression coefficients variancedecomposition proportion [41]. High variance decompositionproportion of two or more regression coefficients associated with a high condition index indicates which variables are potentially involved in the multicollinearity.
Coping with multicollinearity
Multicollinearity may result due to population unrepresentative sample or insufficient information in the sample. For example, if the data do not include relevant variables for the model specification or the sample size is small to evaluate the effects. In these situations the statistical and epidemiological literature suggest to collect more variables, or increase the sample size which theoretically should reduce the standard errors of the slopes. The CCHC study for systolic and diastolic blood pressure illustrated that the large sample size not always result in small standard errors in the presence of a high degree of collinearity. When collinear variables are in a perfect or nearly perfect linear relationship, another approach which follows from the definition of linear dependency13 is to express one of the collinear variables as a function of the other collinear variable, knowing prior quantification of their relationship, combine them in a new variable and use the new variable in the regression model. Other approaches for coping with multicollinearity proposed in the literature are principal component analysis (PCA) [42,43], partial least squares regression (PLS) [44] as an alternative approach to PCA, or ridge regression method [45].
Waist circumference had a non-significant effect on systolic and diastolic blood pressure when evaluated together with BMI. This means that in the presence of the information provided by BMI, WC does not add additional significant information to the prediction of the systolic and diastolic blood pressure. Alternatively, since the effect of WC and BMI cannot be disentangled, the significance of their joint effect on systolic and diastolic blood pressure can be evaluated using two degrees of freedom likelihood-ratio test or Wald test. When the direction of the association between predictors and outcome variable is not important, one can use multivariate General Linear Models (MGLM) [46,47] to assess the joint effect of BMI and WC on systolic and diastolic blood pressure by switching the correlated independent variables BMI and WC with the dependent variable can be used as well. MGLM method has been shown to be highly efficient in reducing and minimizing multicollinearity due to high correlations between independent variables when obtaining estimates of the standard error for estimated regression parameters [48].
Strength and limitations
The simulation study was designed to represent closely the CCHC dataset. The variables used in the simulation were generated to be similar in distribution to that of the systolic blood pressure, BMI, waist circumference, and participant’s age in the CCHC study. Using simulation studies, we demonstrated what would be the impact of different degrees of multicollinearity on regression estimates and statistics in linear regression models. The findings from the analysis of the simulated data aided the interpretation of the findings from the CCHC study. The CCHC study was performed based on available data of 2874 participants which provided adequate power to be able to detect significance of a coefficient estimate for a covariate involved in multicollinearity in a multivariable linear regression analysis. Despite this large sample size, we demonstrated that the effect of the multicollinearity between BMI and WC had very high impact on the findings from the linear regression analysis. Although the work presented here is based on linear regression models, the findings from this study are generalizable to other regression models including Cox proportional-hazards, logistic, Poisson, and Negative binomial regression models.
Our studies have some limitations. These studies illustrated a multicollinearity effect between continuous variables. However in practice multicollinearity effect may occur between continuous and categorical, or categorical only variables. In addition, since the main purpose of the study was to demonstrate the role of multicollinearity in regression analysis in the presence of correlated predictors we did not use the developed sampling weights from the CCHC which were created to account for imbalances in the distribution of sex and age due to unequal participation of household members in the census tracts and to scale the sample to the population [29].
Conclusions
A majority of researchers do not report multicollinearity diagnostic when analyzing data using regression models. Using simulated datasets and real life data from the Cameron County Hispanic Cohort, we have demonstrated the adverse effects of multicollinearity in the regression analysis and encourage researchers to consider the diagnostic for multicollinearity as one of the major steps in the regression analysis process. Based on our simulation and CCHC study we recommend that along with the bivariate correlation coefficients between the predictors in the model and the VIFs, researchers should always examine the changes in the coefficient estimates along with the changes in their standard errors and even the changes in VIF. VIF less than 5 (VIF<5) does not always indicate low multicollinearity. A caution must be taken when more than two predictors in the model have even weak pairwise correlation coefficients (r=0.25) as they can result in a significant multicollinearity effect.
Acknowledgments
Part of this work was supported by the Center for Clinical and Translational Sciences, which is funded by National institutes of Health Clinical and Translational Award UL1 TR000371 from the National Center for Advancing Translational Sciences. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Center for Advancing Translational Sciences or the National Institutes of Health.
Author Contributions
Research idea and study design: KPV, MHR; CCHC data acquisition: JBM; simulation and statistical analysis KPV; interpretation: KPV, MHR; wrote the manuscript: KPV; reviewed/edited manuscript: MHR, ML. Each author: provided intellectual content; contributed significantly to the preparation and/or revision of the manuscript; and approved the final version of the manuscript. KPV takes responsibility for the integrity of the data and the accuracy of the data analysis.
13 A finite set 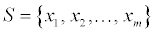 of vectors in Rn is said to be linearly dependent if there exist scalars (real numbers)
of vectors in Rn is said to be linearly dependent if there exist scalars (real numbers) 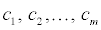 not all of which are 0, such that
not all of which are 0, such that 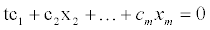
References
- Aiken LS, West SG (1991) Multiple regression: Testing and interpreting interactions. Newbury Park C, editor, SAGE Publications, Inc.
- Gordon RA (1968) Issues in Multiple Regression. The American Journal of Sociology 73: 592-616.
- Stewart GW (1987) Collinearity and Least Squares Regression. Statistical Science 2: 68-100.
- Mason G (1987) Coping with multicollinearity. The Canadian Journal of program evaluation 2.
- Mason Charlotte H, William D, PerreaultJr (1991) Collinearity, Power, and Interpretation of Multiple Regression Analysis. Journal of Marketing Research 28: 268-280.
- Graham MH (2003) Confronting Multicollinearity in Ecological Multiple Regression. Ecology 84: 2809-2815.
- Tu YK, Clerehugh V, Gilthorpe MS (2004) Collinearity in linear regression is a serious problem in oral health research. Eur J Oral Sci 112: 389-397.
- O’Brien RM (2007) A caution regarding rules of thumb for variance inflation factors. Quality and Quantity Springer 41: 673-690.
- Erdeniz B, Rohe T, Done J, Seidler RD (2013) A simple solution for model comparison in bold imaging: the special case of reward prediction error and reward outcomes. Front Neurosci 7: 116.
- Dormann CF, Elith J, Bacher S (2013) Collinearity: a review of methods to deal with it and a simulation study evaluating their performance. Echography 36: 27-46.
- Farrar DE, Glauber RR (1967) Multicollinearity in regression analysis: the problem revisited. Review of Economics and Statistics 49: 92-107.
- Mela CF, Kopalle PK (2002) The impact of collinearity on analysis: the asymmetric effect of negative and positive correlations. Applied Economics 34: 667-677.
- Hoffmann, JP (2010) Linear Regression Analysis: Applications and Assumptions (2nd edn.), Wade Jacobson KB, Brigham Young University.
- Kutner M, Nachtsheim C, Neter J (2004) Applied Linear Statistical Models (4th edn.), McGraw-Hill/Irwin.
- Tamimi RM, Hankinson SE, Campos H, Spiegelman D, Zhang S, et al. (2005) Plasma carotenoids, retinol, and tocopherols and risk of breast cancer. Am J Epidemiol 161: 153-160.
- Leal C, Bean K, Thomas F, Chaix B (2012) Multicollinearity in associations between multiple environmental features and body weight and abdominal fat: using matching techniques to assess whether the associations are separable. Am J Epidemiol 175: 1152-62.
- Fleten C, Nystad W, Stigum H, Skjaerven R, Lawlor DA, et al. (2012) Parent-offspring body mass index associations in the Norwegian Mother and Child Cohort Study: a family-based approach to studying the role of the intrauterine environment in childhood adiposity. Am J Epidemiol 176: 83-92.
- Rotimi C, Cooper R (1995) Familial resemblance for anthropometric measurements and relative fat distribution among African Americans. Int J ObesRelatMetabDisord 19: 875-880.
- Pyke SD, Wood DA, Kinmonth AL, Thompson SG (1997) Change in coronary risk and coronary risk factor levels in couples following lifestyle intervention. The British Family Heart Study. Arch Fam Med 6: 354-360.
- Inoue K, Sawada T, Suge H, Nao Y, Igarashi M (1996) Spouse concordance of obesity, blood pressures and serum risk factors for atherosclerosis. J Hum Hypertens 10: 455-459.
- Jeffery RW, Rick AM (2002) Cross-sectional and longitudinal associations between body mass index and marriage-related factors. below Obes Res 10: 809-815.
- Abrevaya J, Tang H (2011) Body mass index in families: spousal correlation, endogeneity, and intergenerational transmission. Empirical Economics 41: 841-864.
- Desai CS, Colangelo LA, Liu K, Jacobs DR, Cook, et al. (2013) Prevalence, prospective risk markers, and prognosis associated with the presence of left ventricular diastolic dysfunction in young adults: the coronary artery risk development in young adults study. Am J Epidemiol 177: 20-32.
- Mungreiphy NK, Kapoor S, Sinha R (2011) Association between BMI, Blood Pressure, and Age: Study among Tangkhul Naga TribalMales of Northeast India. Hindawi Publishing Corporation Journal of Anthropology.
- Dagan SS, Segev S, Novikov, Dankner R (2013) Waist circumference vs body mass index in association with cardiorespiratory fitness in healthy men and women: a cross sectional analysis of 403 subjects. Nutrition Journal 12.
- Feller S, Boeing H, Pischon T (2010) Body mass index, waist circumference, and the risk of type 2 diabetes mellitus: implications for routine clinical practice. DtschArzteblInt 107: 470-476.
- Janssen I, Katzmarzyk PT, Ross R (2004) Waist circumference and not body mass index explains obesity-related health risk. below Am J ClinNutr 79: 379-384.
- Peters TJ (2008) Multifarious terminology: multivariable or multivariate? univariable or univariate? PediatricPerinatEpidemiol22: 506.
- Fisher-Hoch SP, Rentfro AR, Salinas JJ, Perez A, Brown HS, et al. (2010) Socioeconomic status and prevalence of obesity and diabetes in a Mexican American community, Cameron County, Texas, 2004-2007. Prev Chronic Dis 7: A53.
- Kleinbaum DG, Kupper LL, Nizam A, Muller KE (2008) Applied Regression Analysis and Other Multivariable Methods (4th edn.), Duxbury Press.
- Guimarães IC, de Almeida AM, Santos AS, Barbosa DB, Guimarães AC (2008) Blood pressure: effect of body mass index and of waist circumference on adolescents. Arq Bras Cardiol 90: 393-399.
- Al-Sendi AM, Shetty P, Musaiger AO, Myatt M (2003) Relationship between body composition and blood pressure in Bahraini adolescents. Br J Nutr 90: 837-844.
- Lara M, Bustos P, Amigo H, Silva C, Rona RJ (2012) Is waist circumference a better predictor of blood pressure, insulin resistance and blood lipids than body mass index in young Chilean adults? BMC Public Health 12: 638.
- Song YH (2014) The association of blood pressure with body mass index and waist circumference in normal weight and overweight adolescents. Korean J Pediatr 57: 79-84.
- Donath C, Grässel E, Baier D, Pfeiffer C, Bleich S, et al. (2012) Predictors of binge drinking in adolescents: ultimate and distal factors - a representative study. BMC Public Health 12: 263.
- Berry WD, Feldman S (1985) Multiple Regression in Practice (Quantitative Applications in the Social Sciences). SAGE Publications, Inc.
- Chennamaneni P, Echambadi R, Hess J, Syam N (2008) How Do You Properly Diagnose Harmful Collinearity in Moderated Regressions?
- Belsley DA (1991) Conditioning Diagnostics: Collinearity and Weak Data in Regression(1st edn.), Wiley-Interscience.
- Freund RJ, Wilson WJ (1998) Regression Analysis: Statistical Modeling of a Response Variable (1st edn.), Academic Press.
- Belsley DA, Kuh E, Welsch RE (1980) Regression Diagnostics: Identifying Influential Data and Sources of Collinearity. John WileyandSons, Inc.
- Pearson K (1901) On Lines and Planes of Closest Fit to Systems of Points in Space. Philosophical Magazine 2: 559-572.
- Hotelling H (1933) Analysis of a complex of statistical variables into principal components. Journal of Educational Psychology 24: 417-441, 498-520.
- Wold S, Sjöström M, Eriksson L (2001) PLS-regression: a basic tool of chemometrics. Chemometrics and Intelligent Laboratory Systems 58: 109-130.
- Hoerl AE, Kennard RW (1970) Ridge regression: Applications to nonorthogonal problems. Technometrics12: 55.
- Johnson RA, Wichern DW (2007) Applied multivariate statistical analysis(6th edn.), London: Prentice Hall.
- Haase RF (2011) Multivariate General Linear Models. SAGE Publications, Inc.
- Rahbar MH, Samms-Vaughan M, LovelKA, Pearson DA, Bressler J, et al. (2012) Maternal and paternal age are jointly associated with childhood autism in Jamaica. J Autism DevDisord 42: 1928-1938.
Citation: Vatcheva KP, Lee M, McCormick JB, Rahbar MH (2016) Multicollinearity in Regression Analyses Conducted in Epidemiologic Studies. Epidemiol 6:227. DOI: 10.4172/2161-1165.1000227
Copyright: © 2016 Vatcheva KP, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Select your language of interest to view the total content in your interested language
Share This Article
Recommended Journals
Open Access Journals
Article Tools
Article Usage
- Total views: 27704
- [From(publication date): 4-2016 - Aug 29, 2025]
- Breakdown by view type
- HTML page views: 26079
- PDF downloads: 1625
