Research Article Open Access
Novel Anisotropic Margin Calculation Based On the Cumulative Frequency Distribution of Uncertainties in the Clinical Target Volume
| Ryu Kawamorita1,2*, Hajime Monzen1, Wataru Okada2, Ryuta Nakahara2, Shun Kishimoto2, Kentaro Ishii2, Toshifumi Nakajima2 and Yasumasa Nishimura1 | |
| 1Department of Radiation Oncology, Kinki University, Faculty of Medicine, Osaka-Sayama, Osaka, Japan | |
| 2Department of Radiation Oncology, Tane General Hospital, Osaka-Nishiku, Osaka, Japan. | |
| Corresponding Author : | Ryu Kawamorita Department of Radiation Oncology Tane General Hospital, 1-12-21 Kujo-Minami, Nishi-ku Osaka city, Osaka 550-0025, Japan Tel: +81-6-6581-1071 Fax: +81-6-6585-2772 E-mail: kawamorita@tane.or.jp |
| Received: July 18, 2015 Accepted: August 11, 2015 Published: August 14, 2015 | |
| Citation:Kawamorita R, Monzen H, Okada W, Nakahara R, Kishimoto S, et al. (2015) Novel Anisotropic Margin Calculation Based On the Cumulative Frequency Distribution of Uncertainties in the Clinical Target Volume. OMICS J Radiol 4:202. doi:10.4172/2167-7964.1000202 | |
| Copyright: © 2015 Kawamorita R et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. | |
Visit for more related articles at Journal of Radiology
Abstract
Objective: The purpose of this study was to determine the PTV margins from the cumulative frequency of uncertainties of the clinical target volume (CTV) position obtained using hybrid-image guided radiotherapy (H-IGRT) with volumetric-modulated arc therapy (VMAT).
Materials and Methods: Study participants were 22 patients with intermediate-risk prostate cancer who underwent VMAT. All patients were treated using the following image-guided (IG) procedure: 1) no-correction skin mark setup (no- IG); 2) bony anatomy registration with 2D-imaging (2D-IG); and 3) organ registration using CBCT images (3D-IG). The systematic (Σtot) and random (σtot) errors were obtained from the no-IG, 2D-IG, and 3D-IG registration images of 198 fractions. The PTV margin was computed using the cumulative frequency distribution of the actual position errors of the CTV, and which was compared with the formulation by MPTV = 2.5 Σtot + 0.7 σtot.
Results: The margin size of 3D IG procedure was as follows: 3D-IG: 7.6, 5.4, and 3.5 mm for the AP, SI, and LR axes, respectively. Using MPTV = 2.5 Σtot + 0.7 σtot: 3D-IG: 4.2, 3.7, and 1.3 mm for the AP, SI, and LR axes, respectively. In MPTV: = α Σtot + β σtot, the coefficients α and β were α = 3.4, 2.3, and 4.6 and β = 2.9, 3.0, and 3.0 for AP, SI, and LR, respectively.
Conclusion: The margin size (MPTV) calculated by our modified formulation based on the margin direction satisfied 99% of the prescription dose coverage in each direction and a minimum of 95% of the dose coverage to the CTV for all patients using H-IGRT
| Keywords |
| Hybrid image-guided radiotherapy; Planning target volume margin; Prostate cancer; CTV position uncertainty |
| Introduction |
| Online image guided radiotherapy (IGRT) is used for prostate registration for prostate cancer patients [1-5]. At our hospital, online correction via a three-step setup protocol with hybrid-image guided radiotherapy (H-IGRT) is conducted, i.e., two-dimensional (2D)/ three-dimensional (3D) and 3D/3D registrations are performed using H-IGRT. Our IGRT protocol preferentially uses organ registration relative to the anterior rectal wall, which corrects for almost all systematic errors; however, several random errors remain. Setup correction protocols may reduce geometric treatment uncertainties and the clinical target volume (CTV)-to-planning target volume (PTV) margins. Therefore, a novel approach is required for PTV margin calculations (MPTV) in H-IGRT that accounts for small systematic uncertainty, random uncertainty and target registration residual error (TRE) depend on H-IGRT system, in contrast to the more general formulation by van Herk et al., i.e., MPTV = 2.5 Σ + 0.7 σ, which accounts for the population systematic uncertainty Σ and random uncertainty σ. This formula (MPTV = 2.5 Σ + 0.7 σ) was computed with statistical procedure using systematic and random uncertainties of CTV position [6]. Furthermore, the coefficients of the model parameters were numerically calculated under a spherically symmetric condition thereby leading to an isotropic margin perpendicular to a spherical tumor surface. However, did not consider about residual error to be TRE in case of using IGRT. For example, as TRE arise due to deformation of prostate and/or seminal vesicles even if the registration at CTV using image guidance with CBCT. The purpose of this study was to determine thePTV margins from the cumulative frequency of CTV uncertainties include TRE obtained by an H-IGRT system. |
| Materials and Methods |
| Patients and treatment plan |
| Twenty-two intermediate-risk prostate cancer patients who were treated using VMAT between 2012 and 2013 were included in this study. All patients were immobilized in a position using a vacuum cushion (Vac-Lok; MedTech, Orange City, IA, USA). Computed tomography (CT) scans were acquired with 2.5 mm slice thicknesses using a 16–detector row CT scanner (Optima CT580W; GE Medical Systems, Waukesha, WI, USA) from the lower abdomen to 50.0 mm below the ischial tuberosity. The initial reference markers and associated skin marks were placed at the time of CT simulation. |
| CTV was defined as the entire prostate and the proximal 15.0 mm of the seminal vesicles. PTV was generated by adding an 8.0 mm margin to CTV in all dimensions except posteriorly, where a 5.0 mm margin was used. Contouring of the organ at risk (OAR) included the rectum, bladder, femoral heads, penile bulb, and small bowel, defined according to the Radiation Therapy Oncology Group (RTOG) pelvic normal tissue contouring guidelines [7]. The total prescription dose was 78.0 Gy to thePTV at 2.0 Gy per fraction. Dose normalization was set to thePTV mean dose. The treatment plans were generated using singlearc VMAT (358 degree; 74 sec per rotation). All treatment plans were developed using EclipseTM ver.10.0 planning software (Varian Medical Systems, Palo Alto, CA, USA) for 10 MV photon irradiation. The dose was calculated using the Analytical Anisotropic Algorithm in EclipseTM. |
| To verify leaf motion of each beam or specific patient’s plans, various quality assurance tests were conducted [8,9]. Once the VMAT plan was developed and approved, CT simulation datasets were imported into the ExacTrac® X-ray 6D system (BrainLab AG, Feldkirchen, Germany) for 2D/3D registration using digital reconstructed radiographs (DRRs) of 2D oblique images to the planning CT images [10]. The CT simulation datasets were also imported into the ARIA record and verification system (Varian Medical Systems, Palo Alto, CA, USA) for 3D/3D registration using CBCT images and planning CT images [11,12]. VMAT was delivered using linear accelerators equipped with a high-definition multi-leaf collimator (HD-MLC; spatial resolution: 2.5 mm at the isocenter; Novalis TX; BrainLab AG, Feldkirchen, Germany). The daily treatment time, including image registration from the final image acquisition until the end of irradiation, was 4 to 6 min. Before each fractionation, the bladder and rectum volume were prepared in the same way as at the time of CT simulation. |
| IGRT strategy for prostate cancer at our hospital |
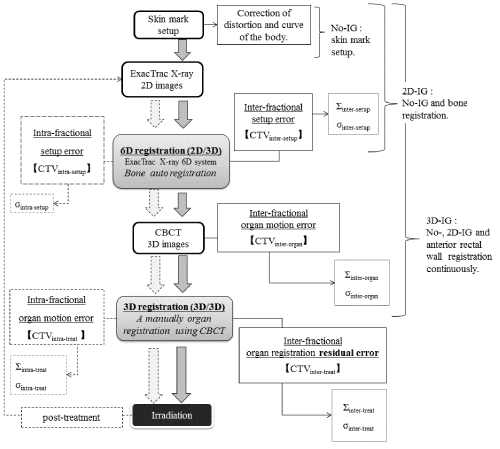
| Figure 1 shows a diagram of the IGRT procedure used in this study. The H-IGRT system consisted of an ExacTrac®X-ray 6D system and linear accelerator equipped with CBCT. All patients were treated using the step-by-step IG procedures involving no-correction skin mark setup (no image guidance; no-IG), bony anatomy 3D registration using 2D images from ExacTrac® X-ray 6D system (2D image guidance; 2D-IG), and 3D organ registration using CBCT images (3D image guidance; 3D-IG). |
| Firstly, the no-IG procedure was used to align the skin mark with the lasers. However, setup residual error of the CTV arose due to geometrical constraints associated with the bony anatomy [11,13]. Also, a systematic pitching error (maximum: 2.0 mm) was present due to the difference between the flexibility of the CT couch and that of the linear accelerator treatment couch. Therefore, as a next step, the 2D-IG procedure using the ExacTrac® X-ray 6D system was used to correct for the setup residual error of the bony anatomy and systematic pitching error of the linear accelerator treatment couch. At the same time, the inter-fractional setup error was calculated by the BrainLab iterative rigid registration process, which uses mutual information as a similarity measure for its calculation [10,11]. Subsequently, interfractional organ motion error was corrected using 3D-IG, with priority given to the anterior rectal wall while simultaneously ensuring that the portion of the rectum overlapping thePTV is excluded. |
| Uncertainty component of the CTV for each image guidance procedure |
| Inter- and intra-fractional variations in the CTV positions relative to the treatment beam were represented as systematic (Σ) or random (σ) uncertainties which were calculated based on components of each CTV in the Table 1, respectively. Σ is the standard deviation of the overall means per patient (M), σ is the overall standard deviation of the population, and Σ and σ uncertainties were calculated from 2D- and 3D-IG image set data. The authors evaluated a total of 396 image sets for inter-fractional variation (198 fractions) and a total of 288 image sets for intra-fractional variation (144 fractions) in the CTV position for the 22 patients. |
| Inter-fractional systematic (Σinter-setup) and random (σinter-setup) setup uncertainties of the bony anatomy were calculated from bony anatomy registration data obtained from 2D-IG images (Figure 1). |
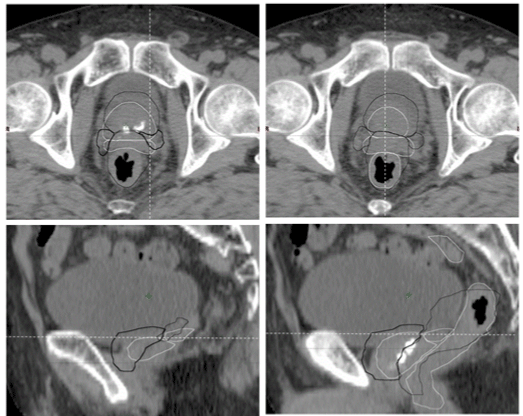
| The CTV position error associated with our setup was categorized into inter- and intra-fractional bony anatomy error (CTVinter-setup and CTVintra-treat [14]. Inter-fractional organ motion systematic (Σinterorg ) and random (σinter-org) uncertainties of the CTV were calculated between the planning CTV position and the CTV position after 2D-IG bony anatomy registration, which was obtained by preregistration of the 3D-IG images; these CTV uncertainty components were defined as CTVinter-organ (Figure 1). Note that Σinter-org and σinter-org include the position error due to deformation [15-17]. Although Σinter-org and σinter-org were corrected using 3D-IG, inter-fractional residual systematic (Σinter-treat ) and random (σinter-treat) uncertainties of the CTV remained due to the anterior rectal wall reference with 3D-IG. Consequently, Σinter-treat and σinter-treat were calculated using the difference between the planning CTV position and the final CTV position used for treatment in the hybrid image guidance (CTVinter-treat), i.e., the final CTV position after the no-IG, 2D-IG, and 3D-IG procedures. As described above, 3DIG was performed with preferential registration given to the anterior rectal wall in this study. Therefore, CTVintra-treat was included in the deformation error of the CTV due to rectal deformation and/or filling as well as inter-fractional prostate motion error (Figure 2). |
| The intra-fractional setup random uncertainty (σintra-setup) was calculated from the pre- and post-treatment position error of the bony anatomy. Systematic (Σintra-treat) and random (σintra-treat) uncertainties for intra-fractional organ motion were calculated from the position error during the CTVintra-treat fraction (CTVintra-treat). σintra-setup, Σintra-treat, and σintra-treat were calculated using image sets of pre- and post-treatment registration of 16 of 22 patients. These intra-fractional uncertainties were obtained using 2D- and 3D-IG images immediately after irradiation. |
| CTVinter-setup, CTVintra-treat, CTVinter-organ, CTVintra-treat, and CTVintra-treat (CTVall) included only translational motion errors related to displacement; rotational angle errors were excluded from evaluation in this study. These five uncertainty components (referred to as CTVall) were included in the residual uncertainty from 3D-IG in addition to the CTV uncertainty reported in the International Committee on Radiation Units (ICRU) Report-62 [18]. The coordinates of CTVall centre were obtained using the isocenter automatic setting function for thePTV. To minimize inter-observer variation, the contouring of organs for definition of the centroid coordinates was performed by a single physicist. |
| Overall systematic (Σtot) and random (σtot) uncertainties |
| The no-IG, 2D-IG, and 3D-IG procedures all had different overall systematic (Σtot) and random (σtot) uncertainty components for the CTV, as shown in Table 1. Σtot and σtot of each IGRT were calculated using the root-sum-square (RSS) of the components of CTVall, as shown in Table 1. Σ, σ, and the mean of these uncertainty components are listed in Table 2; the values for Σ and σ are represented as Gaussian distributions. |
| Equations (1)–(3) were used to calculate Σtot and σtot for thePTV margin size for no-IG, 2D-IG, and 3D-IG (no-PTV margin, 2D-PTV margin, and 3D-PTV margin, respectively) [6]. |
| No-PTV margin: skin mark setup correction. |
| 2D-PTV margin: No-IG and bone corrections using 2D-IG. |
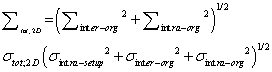 (2) (2) |
| 3D-PTV margin: No-, 2D-IG and organ registration using 3D-IG |
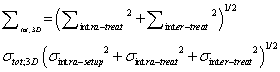 (3) (3) |
| Cumulative frequency distribution of CTVall and PTV margins calculation |
| As described above, the uncertainties associated with CTVall were calculated using the standard deviation of CTVall. van Herk et al. described a PTV margin formula for minimal dose to 95% of the CTV in 90% of the patient population [6], in contrast, the cumulative frequency distributions of the actual CTVall position were obtained to investigate the frequency tolerance level within 80,90,95 and 99% of CTVall. The cumulative frequency distribution was approximated using polynomial regression (R2 > 0.99) fitting. |
| For PTV generation, the CTV is generally expanded with a so-called “rolling ball” algorithm as a spherically symmetric condition [19]. As such, the prostate cancer CTV was considered an organ in the shape of an ellipsoid. Hence, to properly represent the 3D anisotropy of the CTV for a minimal dose prescription of 95% using the cumulative frequency distribution, the tolerance level must be more than 98.5% ; (i.e., the tolerance level was calculated using the formula (95% ≤ (x y z)), where x, y, and z, which correspond to LR, AP, and SI directions, respectively, were 98.5%. From this, the authors used a 99% tolerance level to compute the margin size in each direction for CTVall. |
| To prescribe the minimum dose of the 95% the CTV for each vector of thePTV margin size (MPTV: vector) for each IG procedure (no-IG, 2D-IG, and 3D-IG) was calculated using the RSS of Eq. (4) and the uncertainty components for each IG, shown in Table 1. |
| where m1–m5 were required to describe the margin size of the CTV position uncertainty, computed using cumulative frequency distributions of m1: CTVinter-setup; m2: CTVinter-organ; m3: CTVintra-treat; m4: CTVintra-treat, and m5: CTVintra-treat (Figure 1). The uncertainties with respect to thePTV margin for each IG procedure are listed in Table 1. To compare the margin size with our results, the no-IG, 2D-IG, and 3D-IG PTV margins were calculated using the margin formula of van Herk et al. (M = 2.5 Σtot+0.7 σtot) [6]. |
| Design of the equation to calculate the anisotropic PTV margins for H-IGRT |
| The anisotropic PTV margins can be calculated using the formula MPTV: vector = α Σtot+β σtot. MPTV: vector was calculated at a 99% confidence level based on the cumulative frequency distribution of CTV position error covering more than 95% of the dose distribution for the 3D margin (AP, SI, and LR). Σtot and σtot, the percentage of the CTVall error, and the anisotropy of thePTV margin are given in Tables 3-5, respectively. The formula coefficients α and β for thePTV margin calculation (MPTV:vector = α Σtot+β σtot) were estimated using a least-squares matrix operation. |
| IRB |
| The study design was approved by our institutional review board. |
| Results |
| Systematic (Σ) and random (σ) uncertainties of CTVall |
| The systematic (Σ) and random (σ) uncertainties of CTV for each IG condition are shown in Figure 1. The uncertainty components of the CTV position error with respect to thePTV margin are shown in Table 1. Σ, σ, and the mean of these uncertainty components are listed in Table 2; the values for Σ and σ are represented as Gaussian distributions. The uncertainty of the CTV position for each IG procedure increased in the order AP, SI, and LR for both Σ and σ. According to van Herk et al., Σ for each dimension was larger than σ [6], similar to our results, with Σ having a greater value than σ overall (Table 2). |
| Σtot and σtot values for each IG were computed using Eqs. (1) – (3). For the H-IGRT strategy proposed in this study, systematic and random errors were revised progressively over the IG procedure (no- IG, 2D-IG, and 3D-IG); hence, Σtot and σtot were relatively small after the completion of 3D-IG (Table 3). |
| Although Σtot and σtot for the SI and LR directions for 2D-IG and 3D-IG showed the same results, the individual uncertainty components differed, as shown in Table 1. As described above, the authors adopted the anterior rectal wall registration for the 3D-IG procedure. Therefore, despite prior rectal preparation, rectal filling had an impact on CTV position in 3D-IG; specifically, the LR value was greater than that for 2D-IG. |
| Comparison of thePTV margin sizes using the theoretical formula and actual distributions of the variations in CTV position in our H-IGRT strategy |
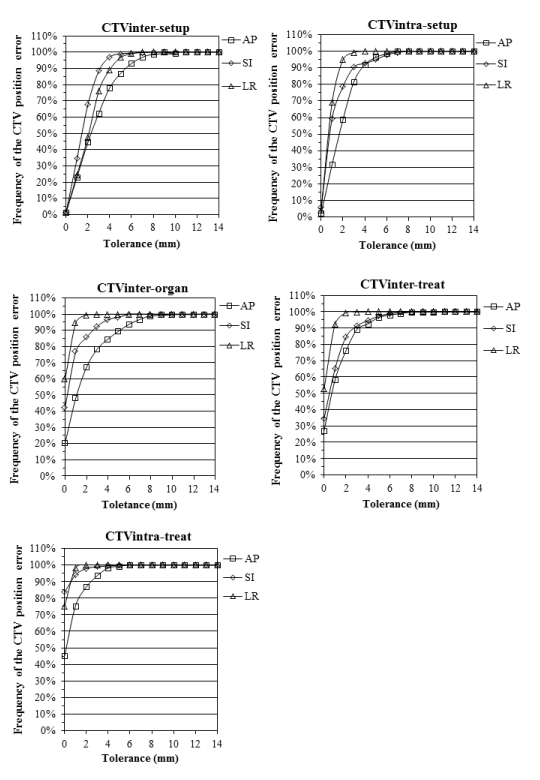
| The cumulative dose frequency distributions of CTV position errors were obtained using inter- and intra-fractional error for CTVall. The curves of the cumulative dose frequency distributions were computed using polynomial regression (R2 > 0.99) fitting (Figure 3). |
| The approximate expressions shown in Figure 3 were then used to compute thePTV margin size within tolerance levels of 80, 90, 95 and 99% for the five components (Table 5). Among the individual components, CTVinter-setup had the greatest influence on PTV margin size, followed by CTVinter-organ, CTVintra-treat, CTVintra-treat, and CTVintra-treat (Table 4). Intra-fractional organ motion and intra-fractional setup uncertainty values (CTVintra-treat and CTVintra-treat) were similar to others> in the literature [20,21]. The maximum position error of the CTV was in the AP direction of CTVinter-setup (>9.0 mm, 99% confidence level). |
| The PTV margins (No-PTV margin, 2D-PTV margin and 3D-PTV margin) were computed using the RSS of the uncertainties of CTV under each IG condition (Tables 1 and 5). The margin sizes corresponding to a 99% tolerance level for a prescription dose of 95% for the anisotropic margin size of CTV are listed in Table 5. |
| The 3D-PTV margin size required for the H-IGRT was 7.6, 5.4, and 3.5 mm in the AP, SI, and LR directions, respectively. Comparing our results for thePTV margin size with those obtained using van Herk’s formulation (MPTV = 2.5 Σtot + 0.7 σtot), our PTV margin was larger in all three directions (Table 6). The maximum difference observed for each IG was as follows: no-IG: 4.3 mm (AP); 2D-IG: 3.0 mm (SI); and 3DIG: 3.3 mm (AP). Using van Herk’s formula, both the 2D- and 3D-PTV margins in the LR direction were 1.3 mm; these sizes are not suitable for clinical use. |
| Design of an anisotropic PTV margin for H-IGRT |
| In this study, α and β in the equation (MPTV = α Σtot + β σtot) were derived for the calculation of the anisotropic PTV margin via H-IGRT. Σtot and σtot were obtained from the uncertainties for CTVall, shown in Table 3. MPTV for a prescription dose of 95% to the CTV was determined using the cumulative frequency distributions of CTVall shown in Table 6. Accordingly, α and β in this equation were computed using a least squares matrix operations (Table 7). Σtot and σtot were reduced during the H-IGRT procedure (Figure 1) due to the progressive corrections that occurred for each process (no-IG, 2D-IG, and 3D-IG). Consequently, for adequate anisotropic PTV margin size calculations, α ranged from 2.3–5.5 and β was 2.8–3.0 (Table 7). |
| Discussion |
| The authors performed online correction using H-IGRT to all fractions for prostate cancer patients undergoing VMAT. The H-IGRT strategy corrected for the systematic and random errors of CTV. The systematic (Σtot) and random uncertainties (σtot), according to the each IG correction protocol were computed with image data sets acquired for inter- and intra-fractional errors of CTV (Tables 1 and 2). Additionally, the proposed PTV margin calculation considered not only inter-fractional prostate movement which was acquired from each IGRT procedure but also a TRE that arise with No-, 2D- and 3D-IG. |
| CTV position exhibits anisotropic variation; thus, thePTV margin size calculation must consider all three dimensions for a minimum dose of more than 95% to the CTV. The CTV is generally expanded with a “rolling ball” algorithm [19] as a spherically symmetric condition in treatment planning for prostate cancer. In this instance, each PTV margin direction should be kept within 98.5% tolerance for a minimum dose of >95% to the CTV. Using the proposed H-IGRT strategy, the 3D-PTV margin size was 7.6, 5.4, and 3.5 mm in the AP, SI, and LR directions, respectively (Table 5), whereas the current PTV margin in the current study (8.0 mm in all dimensions, except posteriorly, where it was 5.0 mm ) were barely reduced. Since the authors are adopting anterior rectal wall registration, rectal side margin will be enough at 5.0 mm. |
| With regard to daily variations in prostate position, several authors described prostate movement of 6.0–20.0 mm in each direction by inter-fractional organ motion or deformation [22-24]; inter-fractional organ motions are larger than intra-fractional motions [25]. Thus, without online IGRT procedures, safety margins of 10.0 mm for the AP and SI directions and 8.0 mm in the LR direction around the prostate have been recommended [1,2]. Hurkmans et al. and Rudat et al. [1,2] computed thePTV margin from actual inter-fractional setup uncertainty; safety margins of 8.0 mm (LR) and 10.0 mm (AP and SI) were reported for prostate cancer patients. Smitsman et al. and Meijer et al. [17,26] considered inter-fractional organ motion uncertainty and residual error of the seminal vesicles in their margin design. |
| In the present study, thePTV margin size was calculated using the cumulative frequency distributions of inter- and intra-fractional variations and TRE, which included the seminal vesicles in the CTV. The margin of the no-IG (only skin mark setup) were 12.6, 7.3, and 5.9 mm for the AP, SI, and LR directions, respectively, calculated using the cumulative frequency distribution of CTVall. Σtot and σtot were substituted into van Herk’s et al. formula (M = 2.5 Σtot+0.7 σtot), and thePTV margin was calculated again, revealing margins of 8.3, 5.0, and 4.4 mm for the AP, SI, and LR directions, respectively. The maximum difference between those results and ours was observed in the AP direction. Also, the 2D- and 3D-PTV margins using van Herk et al. were 1.7–3.4 mm smaller than our results (Table 6). Meijer et al. [26] computed thePTV margin size using a model-based deformable image registration and online IGRT, and compared their results with van Herk et al. [6], whose values were reportedly smaller by a maximum of 3.0, 2.0, and 2.0 mm in the AP, SI, and LR directions, respectively. Coverage in each direction of the CTV computed using the margin size formula proposed by van Herk et al. was no more than 80–95%, with 3D coverage limited to 51–86% (Tables 5 and 6). |
| Engels et al. [27] analysed the correlation of thePTV margin size and impact on the five-year freedom from biochemical failure (FFBF) in IGRT for prostate cancer. The PTV margins of 5.0, 4.0, and 3.0 mm (AP, SI, and LR, respectively) were compared with an isotropic PTV margin of 6.0 mm in all directions; PTV margins of 6.0 mm in all directions indicated a five-year FFBF percentage of 96%, compared with 74% for the tighter PTV margin group. In our results, thePTV margin sizes with MPTV=2.5 Σtot+0.7 σtot were 4.2, 3.7 and 1.3 mm (in the AP, SI, and LR directions, respectively); thus, thePTV margin may be inadequate if van Herk et al.’s formula is used for H-IGRT. Given this margin size, the coverage would range from 51 to 86% for the 3D CTV. Hence, the authors concluded that the use of the MPTV=2.5 Σtot+0.7 σtot formula for prostate cancer may be inadequate. |
| Van Herk et al. assumed that organ movement could be represented by a normal probability distribution; the margin recipe was represented with one formula for all directions for thePTV calculation. In contrast, our recipe offers greater flexibility in that it can accommodate random variation using a cumulative distribution function, because uncertainty of CTV position of the respective direction has a certain variance and distribution. Additionally, H-IGRT can cover variations in the CTV position for each vector, using our recipe, by correcting for nearly all associated systematic errors. More specifically, assuming that Σ is zero by use of the H-IGRT system, and then the calculation for thePTV margin size considers only the random uncertainty (σ), which is simply multiplied by a coefficient value, ranges from 2.8–3.0 to the σ. In this study, the proposed method considers equations for thePTV margin calculation for No, 2D and 3D-IGRT in three axes, AP, SI, and LR. |
| Conclusion |
| H-IGRT was corrected for systematic and random errors of the CTV for almost all fractions. The margin size (MPTV) was calculated using a novel formula that accounted for the anisotropy of the organ considered (the prostate); the recipe satisfied a 99% prescription dose in three directions (AP, SI, and LR). Moreover, using the H-IGRT procedure, the minimum dose to the CTV was 95% of the prescribed dose over three dimensions for all prostate cancer patients. |
| Acknowledgment |
| The authors would like to thank their colleagues for their support in the data analysis. |
| Funding |
| This study was supported in part by a Grant-in-Aid for Cancer Research (H26- 090) from the Ministry of Health, Labour and Welfare of Japan, and by the National Cancer Centre Research and Development Fund (26-A-4). |
References
- Hurkmans CW, Remeijer P, Lebesque JV, Mijnheer BJ (2001) Set-up verification using portal imaging; review of current clinical practice. RadiotherOncol 58: 105-120.
- Rudat V, Flentje M, Oetzel D, Menke M, Schlegel W, et al. (1994) Influence of the positioning error on 3D conformal dose distributions during fractionated radiotherapy. RadiotherOncol 33: 56-63.
- de Crevoisier R, Tucker SL, Dong L, Mohan R, Cheung R, et al. (2005) Increased risk of biochemical and local failure in patients with distended rectum on the planning CT for prostate cancer radiotherapy. Int J RadiatOncolBiolPhys 62: 965-973.
- Wong JR, Grimm L, Uematsu M, Oren R, Cheng CW, et al. (2005) Image-guided radiotherapy for prostate cancer by CT-linear accelerator combination: prostate movements and dosimetric considerations. Int J RadiatOncolBiolPhys 61: 561-569.
- Ghilezan M, Yan D, Liang J, Jaffray D, Wong J, et al. (2004) Online image-guided intensity-modulated radiotherapy for prostate cancer: How much improvement can we expect? A theoretical assessment of clinical benefits and potential dose escalation by improving precision and accuracy of radiation delivery. Int J RadiatOncolBiolPhys 60: 1602-1610.
- vanHerk M, Remeijer P, Rasch C, Lebesque JV (2000) The probability of correct target dosage: dose-population histograms for deriving treatment margins in radiotherapy. Int J RadiatOncolBiolPhys 47: 1121-1135.
- Gay HA, Barthold HJ, O'Meara E, Bosch WR, El Naqa I, et al. (2012) Pelvic normal tissue contouring guidelines for radiation therapy: a Radiation Therapy Oncology Group consensus panel atlas. Int J RadiatOncolBiolPhys 83: e353-362.
- Suzuki M, Nishimura Y, Nakamatsu K, Okumura M, Hashiba H, et al. (2006) Analysis of interfractional set-up errors and intrafractional organ motions during IMRT for head and neck tumors to define an appropriate planning target volume (PTV)- and planning organs at risk volume (PRV)-margins. RadiotherOncol 78: 283-290.
- Suzuki M, Nakamatsu K, Kanamori S, Okumra M, Uchiyama T, et al. (2003) Feasibility study of the simultaneous integrated boost (SIB) method for malignant gliomas using intensity-modulated radiotherapy (IMRT). Jpn J ClinOncol 33: 271-277.
- Jin JY, Yin FF, Tenn SE, Medin PM, Solberg TD (2008) Use of the BrainLABExacTrac X-Ray 6D system in image-guided radiotherapy. Med Dosim 33: 124-134.
- Mayyas E, Chetty IJ, Chetvertkov M, Wen N, Neicu T, et al. (2013) Evaluation of multiple image-based modalities for image-guided radiation therapy (IGRT) of prostate carcinoma: a prospective study. Med Phys 40: 041707.
- Dogan N, Song S, Saleh H, Wu J, Murphy MJ (2010) Comparisons of multiple automated anatomy-based image-guidance methods for patient setup before head/neck external beam radiotherapy. J ApplClin Med Phys 12: 3337.
- Wong JR, Gao Z, Uematsu M, Merrick S, Machernis NP, et al. (2008) Interfractional prostate shifts: review of 1870 computed tomography (CT) scans obtained during image-guided radiotherapy using CT-on-rails for the treatment of prostate cancer. Int J RadiatOncolBiolPhys 72: 1396-1401.
- Schallenkamp JM, Herman MG, Kruse JJ, Pisansky TM (2005) Prostate position relative to pelvic bony anatomy based on intraprostatic gold markers and electronic portal imaging. Int J RadiatOncolBiolPhys 63: 800-811.
- Huang E, Dong L, Chandra A, Kuban DA, Rosen II, et al. (2002) Intrafraction prostate motion during IMRT for prostate cancer. Int J RadiatOncolBiolPhys 53: 261-268.
- Boda-Heggemann J, Köhler FM, Küpper B, Wolff D, Wertz H, et al. (2008) Accuracy of ultrasound-based (BAT) prostate-repositioning: a three-dimensional on-line fiducial-based assessment with cone-beam computed tomography. Int J RadiatOncolBiolPhys 70: 1247-1255.
- Smitsmans MH, de Bois J, Sonke JJ, Catton CN, Jaffray DA, et al. (2011) Residual seminal vesicle displacement in marker-based image-guided radiotherapy for prostate cancer and the impact on margin design. Int J RadiatOncolBiolPhys 80: 590-596.
- ICRU (1999) International Commission in Radiation Units and Measurements, "Prescribing, recording, and reporting photon beam therapy Report-62.
- Remeijer P, Rasch C, Lebesque JV, van Herk M (2002) Margins for translational and rotational uncertainties: a probability-based approach. Int J RadiatOncolBiolPhys 53: 464-474.
- Mah D, Freedman G, Milestone B, Hanlon A, Palacio E, et al. (2002) Measurement of intrafractional prostate motion using magnetic resonance imaging. Int J RadiatOncolBiolPhys 54: 568-575.
- Xie Y, Djajaputra D, King CR, Hossain S, Ma L, et al. (2008) Intrafractional motion of the prostate during hypofractionated radiotherapy. Int J RadiatOncolBiolPhys 72: 236-246.
- Graf R, Boehmer D, Budach V, Wust P (2012) Interfraction rotation of the prostate as evaluated by kilovoltage X-ray fiducial marker imaging in intensity-modulated radiotherapy of localized prostate cancer. Med Dosim 37: 396-400.
- Ghilezan MJ, Jaffray DA, Siewerdsen JH, Van Herk M, Shetty A, et al. (2005) Prostate gland motion assessed with cine-magnetic resonance imaging (cine-MRI). Int J RadiatOncolBiolPhys 62: 406-417.
- Nichol AM, Brock KK, Lockwood GA, Moseley DJ, Rosewall T, et al. (2007) A magnetic resonance imaging study of prostate deformation relative to implanted gold fiducial markers. Int J RadiatOncolBiolPhys 67: 48-56.
- Balter JM, Sandler HM, Lam K, Bree RL, Lichter AS, et al. (1995) Measurement of prostate movement over the course of routine radiotherapy using implanted markers. Int J RadiatOncolBiolPhys 31: 113-118.
- Meijer GJ, de Klerk J, Bzdusek K, van den Berg HA, Janssen R, et al. (2008) What CTV-to-PTV margins should be applied for prostate irradiation? Four-dimensional quantitative assessment using model-based deformable image registration techniques. Int J RadiatOncolBiolPhys 72: 1416-1425.
- Engels B, Soete G, Gevaert T, Storme G, Michielsen D, et al. (2014) Impact of planning target volume margins and rectal distent ion on biochemical failure in image-guided radiotherapy of prostate cancer. RadiotherOncol 111: 106-109.
Tables and Figures at a glance
| Table 1 | Table 2 | Table 3 | Table 4 |
| Table 5 | Table 6 | Table 7 |
Figures at a glance
 |
 |
 |
| Figure 1 | Figure 2 | Figure 3 |
Relevant Topics
- Abdominal Radiology
- AI in Radiology
- Breast Imaging
- Cardiovascular Radiology
- Chest Radiology
- Clinical Radiology
- CT Imaging
- Diagnostic Radiology
- Emergency Radiology
- Fluoroscopy Radiology
- General Radiology
- Genitourinary Radiology
- Interventional Radiology Techniques
- Mammography
- Minimal Invasive surgery
- Musculoskeletal Radiology
- Neuroradiology
- Neuroradiology Advances
- Oral and Maxillofacial Radiology
- Radiography
- Radiology Imaging
- Surgical Radiology
- Tele Radiology
- Therapeutic Radiology
Recommended Journals
Article Tools
Article Usage
- Total views: 15157
- [From(publication date):
August-2015 - Aug 30, 2025] - Breakdown by view type
- HTML page views : 10400
- PDF downloads : 4757
