Research Article Open Access
Optimization of Biosorption of Reactive Blue 222 by Dead Biomass of Rhizopus arrhizus NCIM997 Using Response Surface Methodology
Sukhada Saraf* and Varsha K Vaidya
The Institute of Science, Madam Cama Road, Mumbai, Maharashtra, India
- *Corresponding Author:
- Sukhada Saraf
The Institute of Science
Madam Cama Road
Mumbai-400 032, Maharashtra, India
Tel: +919969574411
E-mail: saraf_sukhada@yahoo.co.in
Received date: February 25, 2016; Accepted date: March 14, 2016; Published date: March 19, 2016
Citation: Saraf S, Vaidya VK (2016) Optimization of Biosorption of Reactive Blue 222 by Dead Biomass of Rhizopus arrhizus NCIM997 Using Response Surface Methodology. Ind Chem 2:118. doi:10.4172/2469-9764.1000118
Copyright: © 2016 Saraf S, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Industrial Chemistry
Abstract
The present investigation deals with utilization of dead fungal biomass of Rhizopus arrhizus NCIM 997 as a low-cost biosorbent and optimization of conditions for the removal of Reactive Blue 222 dye from aqueous solution using sequential statistically designed experiments. Plackett - Burman design with six independent variables (pH, concentration of dye, concentration of biosorbent, temperature, speed of agitation and contact time), was used initially to identify the most significant factors influencing biosorption. Path of Steepest Ascent was then used to move towards the vicinity of optimum operating conditions. Central Composite Design at the specified combinations of four significant factors identified by Plackett–Burman Design (pH, concentration of dye, concentration of biosorbent, contact time) and response surface analysis were then adopted to investigate mutual interactions between these variables and to identify their optimal values. The maximum sorption (72.89 mg g-1) was obtained under following conditions: pH 1.5, initial concentration of dye 88 mgL-1, concentration of biosorbent 1.2 gL-1 and contact time 111 min. Validation experiments showed excellent correlation between predicted and experimental values. The fitted quadratic model was used to arrive at the best operating conditions to achieve a maximum response. The sequential optimization was successfully used to increase biosorption by 12.82%.
Keywords
R. arrhizus; Reactive blue 222; Biosorption; Plackett– Burman design; Path of steepest ascent; Response surface methodology
Introduction
India accounts for 12% of global colorant industry, with production of all types of dyes such as disperse, reactive and direct dyes. These dyes are extensively used in textile, leather, paper, food and plastics industries [1-3]. Cotton occupies the numberone positionamong all the textile fibers, and more than 50% of its production is dyed with reactive azo dyes, owing to their technical characteristics. Textile effluent is characterized by high values of chemical oxygen demand (COD), biological oxygen demand (BOD), suspended and dissolved solids [4]. Most of the dyes escape conventional wastewater treatment processes due to their synthetic origin and complex aromatic molecular structures as well as high stability against light, temperature, chemicals and microbial attack [5]. Moreover, various azo dyes have been shown to be anaerobically decolorized by cleavage of the azo bond, resulting in the formation of potentially carcinogenic aromatic amines.
Adsorption has been observed to be an effective process for color removal from dye wastewater due to its ability to handle large flow rates and productionof a high-quality effluent that does not result in the formation of harmful substances. A large variety of adsorbent materials have been tested to remove dyes including activated carbon, because of its excellent adsorption capacity for organic pollutants. Although it has a good adsorption capacity, difficulty in regeneration and its high costs limit its commercial application (unit cost of virgin material is about US $ 1 kg-1) [6]. Hence, low-cost biosorbent materials with high adsorption capacities have gained increasing attention in minimizing the disposal problem [7]. These alternative adsorbents include industrial/ agricultural/ domestic wastes or by-products such as slag, sludge, fly ash, bagasse etc. as well as biosorbents derived from microbial biomass. Applcication of inactivated fungal biomass to remove textile dyes from effluents offers many advantages such as cheap and continuous supply from various food and industrial fermentation processes, easy storage, more selectivity than traditional ion-exchange resins and activated carbons, high removal rates, low costs and regenerative potential. The efficiency of the biosorption process of reactive azo dyes, under equilibrium conditions by some fungi has been shown to be more than that of activated carbon [6,8].
The adsorption capacity is one of the essential parameters in the process design of a specific adsorbate - adsorbent system. Generally, optimization of adsorption efficiency is carried out by using traditional one factor at a time method, which though simple, consumes time and chemicals in large quantities whileneglecting the interaction effects of process variables which can lead to misinterpretation of results. Compared to it, the advantages of statistical approaches are quite obvious: improved yield reduced process variability, closer confirmation of the output response to normal, reduced development time and reduced overall costs [9]. Statistical approaches can be adopted at various phases of an optimization strategy. Hence, in the present study multi-variant experimental design based on sequential statistical approach was used for techno-economical removal of a dioazo reactive dye, Reactive Blue (RB 222) from an aqueous solution using the dead biomass of Rhizopus arrhizus NCIM 997 as a low-cost biosorbent. It involved stepwise use of a well-established statistical technique for screening critical factors, Plackett–Burman Design (PBD) followed by the use of Path of Steepest Ascent (PSA) to locate the optimum domain of the critical factors and Central Composite Design (CCD) using Response Surface Methodology (RSM). RSM, a collection of statistical techniques was used to build models, to study the interactions between the variables and to select the optimum conditions of variables or desirable responses while minimizing the empiricism of trial-and-error techniques [10]. The combination of both Plackett - Burman Design and Response Surface Methodology has been investigated in recent years, with prominence to studies of the removal of various dyes like Reactive black 5 [11], Reactive red 120 [12], Basic Blue 3, Methylene Blue [13] etc.
In the present study, RB 222 was chosen as a model dye because of its extensive use in Indian textile industry for dyeing and printing cotton, linen, silk and nylon fabric and difficulty in its treatment using traditional processes.
Materials and Methods
Preparation of the biosorbents
A pure strain of filamentous fungus Rhizopus arrhizus (NCIM 997) obtained from National Chemical Laboratory; Pune, India was routinely maintained at 4°C on Potato Dextrose Agar (PDA) (g L-1: Potato infusion from 200 g potatoes, Dextrose 20 g, Yeast extract 0.1, Agar 20, pH 5.0). For biosorption experiments, fungal mycelia were obtained by aseptically transferring mycelia from the PDA spread-plate cultures to 100 mL of Potato Dextrose Broth (PDB) containing 0.25% Tween 80 (to prevent sporulation) in 250 mL Erlenmeyer flasks. The biomass was harvested after seven days of incubation at 30±1°C under static conditions with intermittent shaking. The biomass thus obtained was washed thoroughly with copious amounts of double distilled water and dried at 80°C for 24 h. The size of the biomass particles was kept uniform by grinding into a fine powder and sieving through a 150- mesh sieve. The dried biomass was stored in a desiccator and was used for the biosorption experiments [14].
Preparation of adsorbate
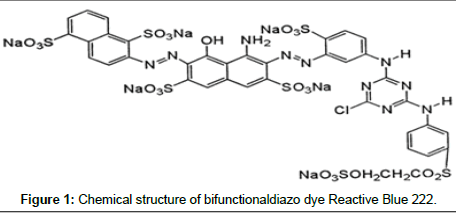
Reactive Navy Blue BF (C.I. Reactive Blue 222, CAS 93051-44- 6, Chemical formula: C37H23ClN10Na6O22S7, MW: 1357.49 g mol-1) a bifunctionaldiazo dye was obtained as a solid powder from Dye Star, India and used without further purification. Its chemical structure can be seen in Figure 1. Dye solution was prepared by dissolving the appropriate amount of RB 222 dye in double distilled water. The preferred pH values of the solutions were obtained using 0.1N HCl or 0.1N NaOH. The pH of the solutions was measured using a pH meter (Control Dynamics, India). All the chemicals and reagents used for experiments were of analytical grade and supplied by HiMedia, Mumbai, India.
Biosorption experiments
The biosorption studies were carried out in duplicate for the evaluation of the biosorbent made from the dead biomass of R. arrhizus for the removal of the RB 222 dye from aqueous solutions. The batch contact biosorptionexperiments were conducted employing the specified combinations of independent variables using sequential statistically designed experiments consisting of Plackett - Burman design (PBD), Path of Steepest Ascent (PSA) and Central Composite Design (CCD). For these experiments, 50 mL of dye solutions at desired concentration, pH and concentration of biosorbent dosage taken in 250 mL Erlenmeyer flasks were kept under agitation in a rotating orbital shaker (Labtop Quality Lab Equipment, India) for desired period of time. After centrifugation at 4000 rmin-1, the remaining concentration of dye in the solution was measured using UV–Vis Spectrophotometer (Shimadzu, Japan UV1800 UV/VIS) at 609 nm corresponding to the maximum absorbance. Simultaneously blank without biosorbent was run as a control. The amount of the dye adsorbed on the fungal biomass at the corresponding equilibrium conditions was determined by using a mass balance equation in terms of specific uptake capacity (SUC):
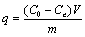 (1)
(1)
Where, q is the amount of dye adsorbed per unit weight of the biosorbent (mgg-1); C0 theinitial concentration of the dye(mgL-1); Ce the concentration of dye in solution at equilibrium time(mgL-1); V the volume of the solution (L); m is the concentration of the biosorbent(g).
Experimental design
Plackett–Burman Design (PBD): To investigate the effects of various parameters like pH, concentration of dye (mg-1), concentration of biosorbent (g -1), temperature (°C), speed of agitation (r min-1) and contact time (min) on the biosorption process, a 12-run Plackett - Burman design was employed along with three runs at zero level. Each variable was examined at two levels: –1 for the low level and +1 for the high level (Table 1) [15].
| Designation | Variable | Variable Values | ||
|---|---|---|---|---|
| -1 | 0 | +1 | ||
| X1 | pH | 2 | 4 | 6 |
| X2 | Concentration of dye (mgL-1) | 40 | 70 | 100 |
| X3 | Concentration of biosorbent(g L-1) | 0.8 | 1.4 | 2.0 |
| X4 | Temperature (°C) | 35 | 40 | 45 |
| X5 | Speed of agitation (r min-1) | 80 | 100 | 120 |
| X6 | Contact time (min) | 30 | 75 | 120 |
Table 1: Levels of the variables tested in Plackett–Burman design for the biosorption of RB 222 dye by R. arrhizus.
The values of the variables were selected based on the previous preliminary experimental results. The Plackett–Burman design and the response value of biosorption are shown in Table 2. All experiments were carried out in duplicate and the average of biosorption SUC (mg g-1) was taken as response. The effect of individual variable on biosorption was calculated by the following Equation (2)
| Run no. | Coded values | SUC(mg g-1) | ||||||
|---|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | X6 | Experimental | Predicted | |
| 1 | +1 | -1 | +1 | -1 | -1 | -1 | 6.82 | 6.86 |
| 2 | +1 | -1 | -1 | -1 | +1 | +1 | 17.23 | 17.72 |
| 3 | -1 | +1 | +1 | -1 | +1 | -1 | 38.26 | 38.46 |
| 4 | +1 | -1 | +1 | +1 | -1 | +1 | 8.56 | 8.43 |
| 5 | +1 | +1 | -1 | +1 | +1 | -1 | 15.01 | 14.88 |
| 6 | +1 | +1 | -1 | +1 | -1 | -1 | 22.27 | 22.46 |
| 7 | -1 | -1 | -1 | +1 | +1 | +1 | 33.47 | 33.36 |
| 8 | -1 | -1 | +1 | +1 | +1 | -1 | 14.90 | 14.92 |
| 9 | -1 | -1 | -1 | -1 | -1 | -1 | 39.51 | 39.38 |
| 10 | -1 | +1 | -1 | -1 | -1 | +1 | 64.61 | 64.48 |
| 11 | +1 | +1 | +1 | -1 | +1 | +1 | 24.66 | 24.38 |
| 12 | -1 | +1 | +1 | +1 | -1 | +1 | 47.26 | 47.6 |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 27.88 | 27.75 |
| 14 | 0 | 0 | 0 | 0 | 0 | 0 | 27.79 | 27.75 |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 | 27.83 | 27.75 |
Table 2: Plackett - Burman experimental design of 12 trials for six variables in high level (+), low level (-) along with observed and predicted values of SUC (mg g-1).
 (2)
(2)
Where, E(Xi) is the effect of the tested variable (Xi) and M+i and M-i are responses (biosorption) of trials at which the variable is at its high or low levels respectively, N is the total number of trials [15].
X1 to X6 as shown in Table 1. Significant factors affecting biosorption were determined from the regression analysis and the contribution of the factors towards the sorption of RB 222 was determined based on the t-value (main effect). The sign of the effect indicates the level at which it was considered for further improvement.
Path of Steepest Ascent (PSA): PSA method is a procedure for moving along the maximum increase in the response. Variables significantly influencing biosorption as identified by PBD experiments were optimized by applying a series of exploratory runs. The direction of steepest ascent is the direction in which the response increases most rapidly by increasing or decreasing the values of the significant factors according to the sign of the main effects. The PSA started from the zero level of variables in the Plackett–Burman experiment and were performed along the steepest ascent path until the response increased no more. This point would be near the optimal point and could be used as center point to optimize the process further using CCD [16].
Response Surface Methodology (RSM): The optimal levels of the significant variables and their interactions on the biosorptionprocess were investigated using CCD (Plackett and Burman). In order to make the design rotatable, a value of α= (nF)1/4=2 was taken. A four factor, five level CCD consisting of 30 runs, with 6 center points (4 cube points and 2 axial points)was conducted in the vicinity of the optimum to locate the true optimum values of pH (X1), initial concentration of dye (X2), concentration of biosorbent (X3) and contact time (X6) (Table 3). The runs were made in a random order to minimize the effects of variability in the observed responses due to extraneous factors. Replicates were used to estimate the experimental error and to check for the adequacy of the model.
| Symbol | Variable | Range and level | ||||
|---|---|---|---|---|---|---|
| -2 | -1 | 0 | +1 | +2 | ||
| X1 | pH | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
| X2 | Concentration of dye (mgL-1) | 79 | 88 | 97 | 106 | 115 |
| X3 | Concentration of biosorbent (gL-1) | 0.9 | 1.0 | 1.1 | 1.2 | 1.3 |
| X6 | Contact time (min) | 84 | 93 | 102 | 111 | 120 |
Table 3: Concentrations of variables at different levels in CCD for biosorption of RB 222 by R. arrhizus.
The factors were coded according to the following Equation (3)
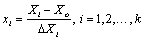 (3)
(3)
Where, xi is the coded value of an independent variable; Xi is thereal value of an independent variable; X0 is the real value of anindependent variable at the center point; and ΔXi is the step changevalue.
The second-order model used to fit the response to the independent variables is shown in Equation (4)
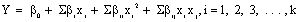 (4)
(4)
Where, is the predictedresponse, and the objective is to optimize the response (Y) . β0 is the constant coefficient, βi is the linear coefficients, βii is the quadratic coefficient, βij is the interaction coefficient, and xi and xj are the coded values of the independent process variables [17,18]. The quality of the polynomial equation was judged by determination coefficient (R2), and its statistical significance was checked by Fischer’s F-test. Analysis of variance (ANOVA) was conducted to determine the significance of the model. The response surface plots of the model predicted responses were utilized to assess the interactive relationships between the significant variables. The results obtained from the statistical analyses of CCD were verified by validation tests, using the predicted optimized conditions against the basal conditions. Minitab 16 (State College, PA, USA) and Design Expert Version 6.0.8 (Stat- Ease Inc., Minneapolis, USA) software were used for experimental design, construction of quadratic models and graphical analysis of the experimental data.
Results and Discussion
Evaluation of operating conditions by PBD
PBD is an efficient two-level screening design, requiring fewer runs than a comparable fractional design and can be used to identify the more important independent variables from a list of candidate factors. It allows unbiased estimation of main effects with smallest possible variance of components. The PBD is based on the first-order model, with no interaction among the factors [15,19]. The data represented in Table 2 shows a wide range of SUC values i.e., from 6.82 to 64.6 l mgg-1 in 12 run trial. Regression analysis was performed on the results and the first order polynomial equation was derived (Equation 5)
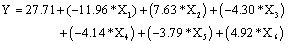 (5)
(5)
R2=0.9997 R2 (pred)=0.9994R2 adj=0.9896
Analyses of the regression coefficients and the t-values of six factors were carried out to study the contribution of each factor towards biosorption (Table 4). The factor with the highest t- value is considered to be the best and is ranked one. Based on the t- values, the variables were ranked in the following order: pH, concentration of dye, contact time, concentration of biosorbent, temperature and speed of agitation. The variable with the large coefficient, either positive or negative, indicates a large impact on the response. A positive sign of the effect of the tested variable indicates its greater influence on biosorption at a high level and a negative effect indicates greater influence of the variable at a low level. Analysis of the regression coefficients of six variables showed that initial concentration of dye (X2) and contact time (X6) had positive effect on biosorption, whereas pH (X1), concentration of biosorbent (X3), temperature (X4) and speed of agitation (X5) had a negative effect on biosorption. The corresponding probability values (P values) indicate the significance of each coefficient. In general, the larger the magnitude of t and smaller the value of P, the more important is the corresponding coefficient term [19]. Table 4 shows that all the parameters are significant (P<0.001) suggesting the significance of the model. The coefficient of determination R2 of 0.9997, implied a good agreement between the experimental and predicted values of SUC and indicated that 99.97% of the total variability in the response could be explained using this model.
| Variables | Effect | Coefficient | Standard Error | t Statistics | P- value |
|---|---|---|---|---|---|
| Intercept | 27.71 | 0.05 | 490.97 | 0 | |
| Block | -0.03 | 0.05 | -0.64 | 0.532 | |
| pH | -23.91 | -11.96 | 0.05 | -211.82 | 0.000 |
| Concentration of dye (mgL-1) | 15.26 | 7.63 | 0.05 | 135.23 | 0.000 |
| Concentration of biosorbent(g L-1) | -8.61 | -4.30 | 0.05 | -76.24 | 0.000 |
| Temperature (°C) | -8.27 | -4.14 | 0.05 | -73.27 | 0.000 |
| Speed of agitation (r min-1) | -7.58 | -3.79 | 0.05 | -67.15 | 0.000 |
| Contact time (min) | 9.84 | 4.92 | 0.05 | 87.14 | 0.000 |
Table 4: Linear multiple regression analysis of Plackett–Burman experiments for the biosorption of RB 222 dye by R. arrhizus.
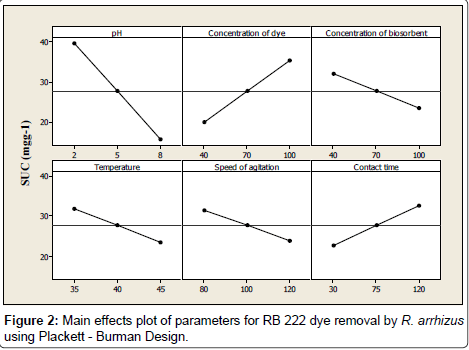
An analysis of the effects of variables on biosorption was carried out using the main effects plot of all the variables used in this work to plot data means and also to compare magnitudes of marginal means as shown in Figure 2.
A main effect occurs when the mean response changes across the levels of a factor. In the main effects plot, a horizontal line (parallel to the x-axis), represents no main effect, while a non-horizontal line indicates a main effect. The magnitude of the main effect is indicated by the steepness of the slope of the line. Analysis of the main effects plot showed that the pH of the solution was the most influential factor in the RB 222 dye removal exerting a negative effect on biosorption. A decrease of 60.27% in SUC was observed when pH was increased from -1 level to +1 level. The pH of the solution is known to play an important role in the whole biosorption process and particularly on the biosorption capacity, affecting the surface charge of the biosorbent, the degree of ionization of the dye present in the solution and the dissociation of the functional groups on the active sites of biosorbent [20,21]. Other variables such as concentration of biosorbent, temperature and speed of agitation also exerted a negative effect on biosorptionshowing a decrease in SUC with increase in the levels of these variables from -1 to +1. On the other hand, a direct relationship was observed between concentration of dye and contact time where increase in their values caused an increase in SUC of the biosorbent. From Figure 2, it is clear that though all the variables played an important role in the adsorption of RB 222; pH, concentration of dye, concentration of biosorbent and contact time seemed to be more dominant factors and were considered in the experiments of PSA and CCD. The highest response of SUC of 64.61 mgg-1 was obtained, after running Plackett- Burman experiments, under following conditions: pH 2.0; concentration of dye 100 mgL-1; concentration of biosorbent 0.8 g L-1; temperature 35°C; speed of agitation 80 r min-1 and contact time 120 min (Table 5).
| Run no. | pH | Concentration of dye(mg g-1) | Concentration of biosorbent(g L-1) | Contact time (min) |
SUC (mg g-1) |
|---|---|---|---|---|---|
| X1 | X2 | X3 | X6 | ||
| 1 | 5 | 70 | 1.4 | 75 | 1.98 |
| 2 | 4 | 79 | 1.3 | 84 | 3.34 |
| 3 | 3 | 88 | 1.2 | 93 | 40.28 |
| 4 | 2 | 97 | 1.1 | 102 | 69.86 |
| 5 | 1 | 106 | 1.0 | 111 | 62.99 |
Table 5: Experimental design and response value of path of steepest ascent for the biosorption of RB 222 dye by R. arrhizus.
Path of Steepest Ascent (PSA)
The PBD experiment though proved to be a valuable tool for screening significant variables that affected RB 222 dye biosorption; it was unable to predict the optimum levels of the variables. Hence, on the basis of the first-order model (Equation 5), the path of steepest ascent and the direction of significant variables were determined by increasing or decreasing the concentrations of the selected variables. The path of steepest ascent started from the center of the PBD and moved along the path in which the pH and concentration of biosorbent decreased and concentration of dye and contact time increased. The less significant factors (temperature and speed of agitation) not considered in PSA were used in all trials at their (−1) level for their negative contribution.
The highest biosorption (SUC) was found to be of 69.86 mg g-1 with pH 2.0; initial concentration of dye 97 mgL-1; concentration of biosorbent 1.1 g L-1 and contact time 102 min (Run No. 4). This point was envisaged to in the vicinity of the optimal and hence was chosen for further optimization by RSM using CCD.
Central Composite Design (CCD)
Once the ranges of the relevant variables selected through the Plackett - Burman screening were narrowed down by PSA and significant gross curvature had been detected in the design space, RSM consisting of trials plus a star configuration was used to appraise quadratic model and central points to estimate the pure process variability and reassess gross curvature. Specified combination of four independent significant factors (pH, concentration of dye, concentration of biosorbent and contact time) at five levels (- 2, -1, 0, +1, +2) were used in CCD experimentsto determine their optimum levels and to study the interactions between them. The design matrix of tested variables in 30 experimental runs along with the experimental results and the results of theoretically predicted responses (using the model equation) are shown in Table 6.
| Run No. |
pH | Concentration of dye (mg g-1) |
Concentration of biosorbent (g L-1) |
Contact time (min) |
SUC (mg g-1) | |
|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X6 | Experimental | Predicted | |
| 1 | -1 | +1 | +1 | -1 | 67.64 | 67.75 |
| 2 | -1 | -1 | +1 | -1 | 71.50 | 71.36 |
| 3 | -1 | +1 | +1 | +1 | 65.90 | 66.63 |
| 4 | +1 | -1 | -1 | +1 | 62.83 | 62.91 |
| 5 | +1 | -1 | -1 | -1 | 57.35 | 56.78 |
| 6 | +1 | -1 | +1 | -1 | 55.59 | 56.19 |
| 7 | -1 | -1 | -1 | +1 | 61.27 | 61.64 |
| 8 | -1 | -1 | +1 | +1 | 72.89 | 73.44 |
| 9 | -1 | +1 | -1 | -1 | 68.25 | 68.53 |
| 10 | +1 | +1 | +1 | -1 | 56.32 | 56.12 |
| 11 | -1 | -1 | -1 | -1 | 67.49 | 68.12 |
| 12 | +1 | +1 | -1 | +1 | 69.55 | 69.85 |
| 13 | +1 | +1 | -1 | -1 | 61.08 | 60.74 |
| 14 | +1 | +1 | +1 | +1 | 61.87 | 61.44 |
| 15 | -1 | +1 | -1 | +1 | 71.60 | 71.21 |
| 16 | +1 | -1 | +1 | +1 | 64.82 | 64.71 |
| 17 | 0 | 0 | 0 | -2 | 60.65 | 60.65 |
| 18 | +2 | 0 | 0 | 0 | 46.72 | 47.24 |
| 19 | 0 | 0 | +2 | 0 | 69.07 | 68.70 |
| 20 | 0 | 0 | 0 | +2 | 66.03 | 65.67 |
| 21 | 0 | +2 | 0 | 0 | 68.05 | 68.21 |
| 22 | 0 | 0 | -2 | 0 | 67.69 | 67.69 |
| 23 | -2 | 0 | 0 | 0 | 64.66 | 63.77 |
| 24 | 0 | -2 | 0 | 0 | 71.58 | 71.06 |
| 25 | 0 | 0 | 0 | 0 | 65.68 | 65.62 |
| 26 | 0 | 0 | 0 | 0 | 66.68 | 65.62 |
| 27 | 0 | 0 | 0 | 0 | 65.68 | 65.62 |
| 28 | 0 | 0 | 0 | 0 | 65.71 | 65.89 |
| 29 | 0 | 0 | 0 | 0 | 68.14 | 68.38 |
| 30 | 0 | 0 | 0 | 0 | 67.14 | 68.38 |
Table 6: Central composite design matrix with experimental and predicted values for the biosorption of RB 222 by R. arrhizus.
R2=0.992 R2 Adj=0.983 R2 Pred=0.978
As seen in Run No. 8 increased biosorption values from 69.86 to 72.89 mg g-1 were obtained using following conditions: pH 1.5; concentration of dye 88 mgL-1; concentration of biosorbent 1.2 g L-1 and contact time 111 min. The data were analyzed using multiple regression analysis in order to obtain an empirical model for the best response and to derive a second-order polynomial equation (Equation 6) as follows:
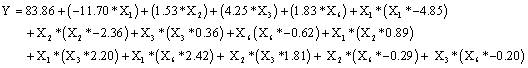 (6)
(6)
RSM gives an insight into the quadratic and interaction effect of the parameters apart from the linear effect of the factors on the dye removal. The analyses were performed by using Fisher's F test and Student’s t test. The regression coefficient, the F and P values for all the linear, quadratic, and interaction effects of the factors used in the study are given in Table 7.
| Term | Coefficient | SE coefficient | t | p |
|---|---|---|---|---|
| Constant | 83.855 | 1.3451 | 62.339 | 0.000 |
| Block | -0.8058 | 0.6302 | -1.279 | 0.222 |
| pH | -11.6995 | 0.6643 | -17.611 | 0.000 |
| Concentration of dye | 1.5318 | 0.6643 | 2.306 | 0.037 |
| Concentration of biosorbent | -4.2509 | 0.6643 | -6.399 | 0.000 |
| Contact time | 1.8291 | 0.6643 | 2.753 | 0.016 |
| pH*pH | -4.8548 | 0.6214 | -7.812 | 0.000 |
| Concentration of dye*Concentration of dye | -2.3582 | 0.6214 | -3.795 | 0.002 |
| Concentration of biosorbent*Concentration of biosorbent | 0.3633 | 0.6214 | 0.585 | 0.568 |
| Contact time*Contact time | -0.6161 | 0.6214 | -0.992 | 0.338 |
| pH*Concentration of dye | 0.8873 | 0.8136 | 1.091 | 0.294 |
| pH*Concentration of biosorbent | 2.2042 | 0.8136 | 2.709 | 0.017 |
| pH*Contact time | 2.4248 | 0.8136 | 2.98 | 0.01 |
| Concentration of dye*Concentration of biosorbent | 1.8131 | 0.8136 | 2.228 | 0.043 |
| Concentration of dye*Contact time | -0.2921 | 0.8136 | -0.359 | 0.725 |
| Concentration of biosorbent*Contact time | -0.2052 | 0.8136 | -0.252 | 0.805 |
Table 7: Estimated regression coefficients and corresponding t and P values of the CCD for the biosorption of RB 222 dye by R. arrhizus.
P< 0.05 for all the linear, quadratic (except for concentration of biosorbent and contact time) as well as interaction effects (except for pH and Concentration of dye; concentration of dye and contact time and concentration of biosorbentand contact time) indicated that they were highly significant and the accuracy and general ability of the polynomial model was good. The analysis of the response trends using the model was reasonable. In order to ensure the statistical significance of quadratic modelemployed for explaining the experimental data at a 95% confidencelevel the model was tested by analysis of variance (ANOVA) results [22] (Table 8).
| Source | DF | Seq SS | Adj SS | Adj MS | F | P |
|---|---|---|---|---|---|---|
| Blocks | 1 | 17.31 | 17.31 | 17.314 | 1.63 | 0.222 |
| Regression | 14 | 4864.58 | 4864.58 | 347.47 | 32.81 | 0 |
| Linear | 4 | 3855.37 | 3855.37 | 963.843 | 91 | 0 |
| Square | 4 | 770.16 | 770.16 | 192.541 | 18.18 | 0 |
| Interaction | 6 | 239.04 | 239.04 | 39.84 | 3.76 | 0.019 |
| Residual Error | 14 | 148.28 | 148.28 | 10.592 | ||
| Lack-of-Fit | 10 | 142.48 | 142.48 | 14.248 | 9.83 | 0.021 |
| Pure Error | 4 | 5.8 | 5.8 | 1.45 | ||
| Total | 29 | 5030.18 |
Table 8: ANOVA for response surface quadratic model.
R2 = 0.9924; Adj-R2=0.9831; Pred-R2 = 0.97; CV= 1.31%; Yield Predicted P<0.0001
DF: Degree of freedom; SS: Sum of squares; MS: Mean sum of square.
The low P-value of the Fisher’s F-test (Fmodel, 32.81) [(Pmodel>F) = 0.000] demonstrated that the model was highly significant. The lower calculated F14,14-value (8.99) than the tabulated F-value even at the 0.0001 confidence level showed a statistically insignificant lack of fit. The model was found to be adequate for prediction within the range of variables employed. The values of R2 and Adj-R2 are close to 1.0, which is very high and advocates a high correlation between the observed values and the predicted values. This indicates that the regression model provides an excellent explanation of the relationship between the independent variables and the response. The R2 also indicated that only 0.76% of the total variations could not be explained by the model. The pred-R2 of 0.97 was in reasonable agreement with adj-R2 of 0.98 indicating that the model is significant. The adjusted coefficient of determination represents the proportion of the variation in the response explained by the regression model. It is thus envisaged that Equation 6 can capture 98.31% of the variation in the measured values of SUC as function of the four independent variables within the ranges considered in the present study. The value of CV (1.31%) demonstrated that the performed experiments were reliable. "Adeq Precision" measures the signal to noise ratio and a ratio value greater than 4 is desirable. A ratio of 18.158 obtained in this study indicated an adequate signal. Therefore, this model can be used to navigate the design space. The ANOVA thus indicated that the second-order polynomial model was highly significant and adequate to represent the actual relationship between the response (SUC mg g-1) and variables, with P< 0.0001 and a high value of the coefficient of determination (99.24%).
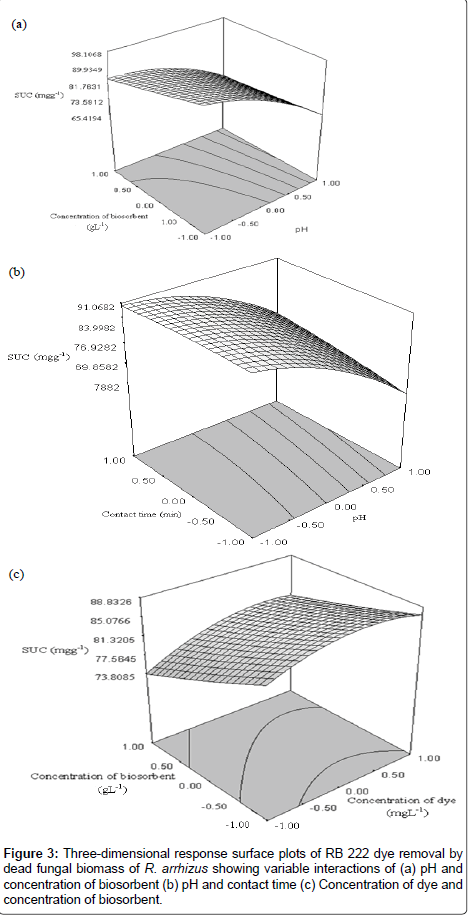
In order to gain a better understanding of the influences ofthe independent variables and their interactions on the dependentvariables, 3D response surface plots for the measured responseswere formed based on the model equation for the removal of RB 222 dye (Figure 3a- 3c) [22]. A surface plot can be used to explore the relationship between three variables. Here, each response surface plot represented the effect of two independent variables varying in the factorial part of the experimental space (between -1 and +1), with the other independent variable set at its central level. These surface plots provide a method to predict the biosorption efficiency for different values of the tested variables.
As seen in Figure 3a-3c, each response surface yield showed a clear peak suggesting that the optimum point was inside the design boundary. Examination of the response surface plot based on independent variables i.e., concentration of biosorbent and pH, with the other independent variable concentration of dye kept at zero level is shown in Figure 3a. The figure revealed an interaction behavior with a negative main effect of both concentration of biosorbent as well as that of pH, where the contribution of pH was prominent compared to that of concentration of biosorbent. This indicated that low concentration of biosorbent and low values of pH yielded high biosorption capacities. The interaction between dye molecules and biosorbent is basically a combined result of charges on dye molecules and the surface of the biosorbent [23]. RB 222 dye is typically an azo-based chromophore combined with different types of reactive groups such as monochloros triazine and β-sulfatoethylsulfone groups that interact with the active groups on the cell surface of the fungal cell wall. The cell wall of the Rhizopus biomass contains hexosamines-chitin and chitosan which constitute approximately 24–40% of the cell dry weight serving as a matrix of -COOH and -NH2 groups, which in turn take part in binding of dyes [24]. As the pH of the solution decreases, more protons are available to protonate the amino groups of chitosan molecules thereby forming positively charged –NH3+ groups. Solution pH other than determining the surface charge of the biosorbent also determines the degree of ionization and speciation of the adsorbate, which affects the adsorption of dyes. Reactive dyes release colored dye anions in solution. The enhancement of uptake of RB 222 dye at acidic pH may be explained in terms of electrostatic interactions between the biomass and the dye ions. Acidic pH increases electrostatic attraction between the anionic group of the RB 222 dye (-SO3-) and the protonated amino group (–NH3+) of chitosan, causing an increase in dye adsorption [7,25,26]. This chemical affinity between the positive charge on the biomass and negative charges in the structures of anionic dye RB 222 weakens the resistance of the boundary layer surrounding the biosorbent leading to more sorption under acidic conditions [27]. In other words at a lower pH, the biomass cell wall is positively charged leading to a decrease in free negatively charged biosorbent sites which are favorable to the adsorption of the negatively charged dye [28]. The deprotonation of surface groups in high pH range results in the electrostatic repulsion between the anionic dye and negatively charged sites contributing to the decreased uptake of RB 222 under alkaline conditions [29,30]. Furthermore, lower adsorption of the dye at higher pH values can be attributed to the competition from excess OH- ions with the anionic dye molecule for the adsorption sites [31].
The competition of the ions for limited available sites causes decrease in the specific uptake capacity with increment in sorbent dose. An important factor at high sorbent dosages is that the available solute is insufficient to completely cover the available exchangeable sites on the biosorbent, usually resulting in low solute uptake [11,32]. Various reasons have been suggested to explain the reduced uptake capacity at increasing concentration of biosorbent such as electrostatic interactions, interference between binding sites, aggregation or overlapping of adsorption sites resulting in a decrease in the total biosorbentsurface area and reduced mixing at higher biomass densities [33-37].
The pH of the dye solution was also involved in a two-way interaction with contact time (Figure 3b) but its main effect remained negative at both levels of contact time. The profile shown in Figure 3b with pH and contact time with the other independent variable concentration of biosorbent kept at zero level, suggests that the SUC of the system increased with decrease in pH value and increase in the contact time. The effect of contact time on the removal of RB222 indicated that a longer contact time favored the reaction towards the equilibrium between the RB 222 and the biosorbent. This may be due to the availability of the uncovered surface area on the biosorbent and the progressive occupation of active binding sites over a longer period of time [31-37].
Figure 3c presents the combination of the parameters: concentration of dye and concentration of biosorbent, with pH at central point. The response surface plot suggested that the initial concentration of dye exerted a positive effect while concentration of biosorbent showed a negative effect on SUC as was evident from an increase in SUC with an increase in concentration of dye from 88 to 106 mgL-1, and decrease in concentration of biosorbent from 1.2 g to 1.0 g L-1. The initial concentration of dye seems to have impact on biosorption through a combination of factors. At higher initial dye concentrations, the dye provides an important driving force to overcome all mass transfer resistances between aqueous and solid phase [20]. Moreover, at higher concentrations of dye, the number of collisions between the dye molecules and the biosorbent increase, thereby allowing the active sites of the biosorbent to be surrounded by a greater number of dye ions, resulting in increased biosorption [38,39].
Validation of the model
To assess the prediction capability of the model developed, several validation experiments were carried out in the region of experimentation delimitated by the factorial points (xi varying between -1 and +1) [9]. The special feature of the RSM tool, 'Point prediction' was employed to find optimum value of the combination of the four factors for the maximum biosorption. The observed values of SUC (72.89 mg g-1) were in good agreement with the predicted values (70.48 mg g-1) and fell into the 95%prediction intervals, further validating the model presented above. The predicted optimal conditions were as follows: pH 1.58, concentration of dye 106 mgL-1, concentration of biosorbents 1.1 g L-1 and contact time 93 min. Thus, the sequential optimization strategy could be successfully employed to increase biosorption by 12.82%.
Conclusion
In the present study, fungal biosorbent R. arrhizus was used successfully for the sorption of reactive diazo dye Reactive Blue 222 from aqueous solution using sequential statistical optimization strategy. Plackett-Burman analysis employed for rapid screening and evaluating critical variables affecting biosorption identified pH, concentration of dye, concentration of biosorbent and contact time as the most significant factors. It allowed unbiased estimation of main effects with smallest possible variance of components. Path of Steepest Ascent was employed to move from the current operating conditions to the optimum region in the most efficient way by using minimum number of experiments. The RSM approach allowed estimation of the influence of the main process variables on biosorption of RB 222 dye and provided useful indications on the optimal set of operating conditions to be used. The excellent correlation between predicted and experimental values confirmed the validity and practicability of this statistical optimum strategy. Thus, the use of RSM approach in combination with a mechanistic model can be a useful tool for a better analysis of dye biosorption data and a more effective design of experiments. The study indicated that the fungal biosorbent is an effective and economical alternative for the removal of the diazo dye RB222 from the aqueous solutions.
References
- Shin M, Nguyen T, Ramsay J (2002) Evaluation of support materials for the surface immobilization and decoloration of amaranth by Trametesversicolor. Appl Microbiol Biotechnol 60: 218-223.
- Ravikumar K, Deebika B, Balu K (2005) Decolourization of aqueous dye solutions by a novel adsorbent: application of statistical designs and surface plots for the optimization and regression analysis. J Hazard Mater 122: 75-83.
- Asamudo NU, Daba AS, Ezeronye OU (2005) Bioremediation of textile effluent using Phanerochaetechrysosporium. Afr J Biotechnol 4: 1548-1553.
- Arun Prasad AS, Bhaskara Rao KV (2010) Physicochemical characterization of textile effluent and screening for dye decolorzing bacteria. Global J Biotech Biochem 5: 80-86.
- Asgher M, Bhatti HN (2012) Evaluation of thermodynamics and effect of chemical treatments on sorption potential of Citrus waste biomass for removal of anionic dyes from aqueous solutions. Ecol Eng 38: 79-85.
- Gupta VK, Suhas (2009) Application of low-cost adsorbents for dye removal--a review. J Environ Manage 90: 2313-2342.
- Chen AH, Chen SM (2009) Biosorption of azo dyes from aqueous solution by glutaraldehyde-crosslinkedchitosans. J Hazard Mater 172: 1111-1121.
- Ambrósio ST, Vilar JC Jr, Silva CA, Okada K, Nascimento AE, et al. (2012) A biosorption isotherm model for the removal of reactive azo dyes by inactivated mycelia of Cunninghamellaelegans UCP 542. Molecules 17: 452-462.
- Zhou J, Yu X, Ding C, Wang Z, Zhou Q, et al. (2011) Optimization of phenol degradation by Candida tropicalis Z-04 using Plackett-Burman design and response surface methodology. J Environ Sci (China) 23: 22-30.
- Box GEP, Hunter WG, Huter JS (1978) Statistics for Experimenters: Design, Innovation, and Discovery, 2ndedn. John Wiley & Sons, USA.
- Vijayaraghavan K, Yun Y (2008) Polysulfone-immobilized Corynebacteriumglutamicum: A biosorbent for Reactive black 5 from aqueous solution in an up-flow packed column. Chem Eng J 145: 44-49.
- Celekli A, Yavuzatmaca M, Bozkurt H (2009) Kinetic and equilibrium studies on the adsorption of reactive red 120 from aqueous solution on Spirogyra majuscule. Chem Eng J 152: 139-145.
- Ong ST, Lee WN, Keng PS, Lee SL, Hung YT (2010) Optimization of basic and reactive dye uptakes in binary dye solution using statistical experimental methodology. Int J Phys Sci 5: 2171-2178.
- Shroff KA, Vaidya VK (2012) Effect of pre-treatments on the biosorption of Chromium (VI) ions by the dead biomass of Rhizopusarrhizus. J ChemTechnolBiotechnol 87: 294-304.
- Plackett RL, Burman JP (1946) The design of optimum multifactorial experiments. Biometrika 33: 305-325.
- Zhang N, Qi Z, Duan H, Xie Y, Yu J, et al. (2012) Optimization of medium composition for production of antifungal active substance from Streptomyces hygroscopicus BS-112.Afr J Microbiol Res 6: 71-80.
- Guo Z, Shen L, Ji Z, Wu W (2012) Enhanced production of a novel cyclic hexapeptide antibiotic (NW-G01) by Streptomyces alboflavus 313 using response surface methodology. Int J MolSci 13: 5230-5241.
- Yazdani M, Bahrami H, Arami M (2014) Preparation and characterization of chitosan/feldspar biohybrid as an adsorbent: optimization of adsorption process via response surface modeling. Scientific World Journal 2014: 370260.
- Montgomery DC (2005) Design and Analysis of Experiments. 6thedn. John Wiley & Sons, New York.
- Aksu Z, Balibek E (2010) Effect of salinity on metal-complex dye biosorption by Rhizopusarrhizus. J Environ Manage 91: 1546-1555.
- Mezenner NY, Hamadi A, Kaddour S, Bensaadi Z, Bensmaili A (2013) Biosorption behavior of Basic Red 46 and Violet 3 by dead Pleurotusmutilus from single- and multi-component systems. J Chem.
- Sener M, Reddy DHK, Kayan B (2014) Biosorption properties of pretreated sporopollenin biomass for lead (II) and copper (II): Application of response surface methodology. Ecol Eng 68: 200-208.
- Maurya NS, Mittal AK, Cornel P, Rother E (2006) Biosorption of dyes using dead macro fungi: effect of dye structure, ionic strength and pH. Bioresour Technol 97: 512-521.
- Tsezos M, Bell JP (1989) Comparison of the biosorption and desorption of hazardous organic pollutants by live and dead biomass. Water Res. 23: 561-568.
- Sun D, Zhang Z, Wang M, Wu Y (2013) Adsorption of reactive dyes on activated carbon developed from Enteromorphaprolifera. Am J Anal Chem 4: 17-26.
- Zheng W, Hu J, Han Z, Wang Z, Zheng Z, et al. (2015) Synthesis of porous carbon fibers with strong anion exchange functional groups. Chem Commun (Camb) 51: 9853-9856.
- Li H, Huang G, An C, Hu J, Yang S (2013) Removal of tannin from aqueous solution by adsorption onto treated coal fly ash: Kinetic, equilibrium, and thermodynamic studies. Ind Eng Chem Res 52: 15923-15931.
- Zille A (2005) Laccase Reactions for Textile Applications. Doctaral Dissertation, Departamento de EngenhariaTêxtil, Escola de Engenharia, Universidade do Minho.
- Zhao DH, Zhang YL, Wei YP, Gao HW (2009) Facile eco-friendly treatment of a dye wastewater mixture by in situ hybridization with growing calcium carbonate. J Mater Chem 19: 7239-7244.
- Wong SY, Tan YP, Abdullah AH, Ong ST (2009) Removal of Basic Blue 3 and Reactive Orange 16 by adsorption onto quartenized sugar cane bagasse. Malaysian J Anal Sci 13: 185-193.
- Ponnusamy SK, Subramaniam R (2013) Process optimization studies of Congo red dye adsorption onto cashew nut shell using response surface methodology. Int J IndChem 4: 17.
- Cardoso NF, Lima EC, Pinto IS, Amavisca CV, Royer B, et al. (2011) Application of cupuassu shell as biosorbent for the removal of textile dyes from aqueous solution. J Environ Manage 92: 1237-1247.
- Gong R, Sun Y, Chen J, Liu H, Yang C (2005) Effect of chemical modification on dye adsorption capacity of peanut hull. Dyes Pigments 67: 175-181.
- Kahraman S, Asma D, Erdemoglu S, Yesilada O (2005) Biosorption of copper by live and dried biomass of Phanerocheatecrysoporium and Funaliatrogii. Eng Life Sci 5: 72-77.
- Baral SS, Das SN, Rath P (2006) Hexavalent chromium removal from aqueous solution by adsorption on treated sawdust. Biochem Eng J 31: 216-222.
- Tewari N, Vasudevan P, Guha BK (2005) Study on biosorption of Cr (VI) by Mucorhiemalis. BiochemEng J 23: 185-192.
- Shroff KA, Vaidya VK (2011) Kinetics and equilibrium studies on biosorption of nickel from aqueous solution by dead fungal biomass of Mucorhiemalis. Chem Eng J 171: 1234-1245.
- Aksakal O,Ucun H (2010) Equilibrium, kinetic and thermodynamic studies of the biosorption of textile dye (Reactive Red 195) onto Pinussylvestris L. J Hazard Mater 181: 666-672.
- Santos O, Castelli CZ, Oliveira MF, Netob A, Meuris GC (2013) Adsorption of synthetic orange dye wastewater in organoclay. Chem Eng Transaction 32: 307-312.
Relevant Topics
Recommended Journals
Article Tools
Article Usage
- Total views: 12342
- [From(publication date):
June-2016 - Aug 18, 2025] - Breakdown by view type
- HTML page views : 11243
- PDF downloads : 1099