Physical Concepts and Ecosystem Ecology: A Revival?
Received: 28-Aug-2018 / Accepted Date: 14-Sep-2018 / Published Date: 21-Sep-2018
Abstract
Ecology has probably borrowed tools and concepts from physics since its origins. Powerful physics approaches have particularly helped incorporate challenges related to ecosystems, including ecosystem functioning and scale issues. I conducted a survey of physical theories and concepts applied to ecosystem ecology to identify fruitful borrowings and past traps. I left aside differential equations and all mathematical tools developed in physics but also used in ecology. Building on information theory, thermodynamics and statistical physics on the one hand, and on dynamical systems, self-organisation, and complexity on the other, my first aim was to identify a trend in this longlasting collaboration between physics and ecology. For example, some physical concepts are now widely recognisedto have failed to help understand and/or to manage an ecosystem as a whole: information theory, thermodynamics and extremal principles belong to this category. More recent physical theories have emerged in ecology and not yet failed: dynamical systems and statistical physics, complexity and graph theories belong to this category.
The second aim of the survey was to identify some of the reasons for the only partial success of otherwise powerful physical concepts in ecology. The ecosystem is a dual object composed of living (biotic) and inert (abiotic) components in close interaction. Although a basic tenet, an ecosystem cannot simply be understood, in practice, as a purely physical (or purely biological) system. Consequently, a difficult theoretical question needs to be addressed: could a revival of the interface between physics and ecology finally reveal how to understand and manage ecosystems? Or will we need radically new concepts (and more generic tools) to understand the ecological organisation of matter and energy in an ecosystem? Strategies for achieving this goal and for advancing theoretical ecosystem ecology are discussed.
Keywords: Thermodynamics; Statistical physics; Complexity; Dynamical system; Graph; Information; Entropy; Self-organisation
Introduction
Physics has long contributed to ecological studies. If we only focus on ecosystems, which are central objects in ecology, physical approaches are one of the main ways to understand and possibly manage ecosystems. We are surrounded by ecosystems, which depend on us, just as we depend on them. The recent acceleration of population growth means increased pressure on ecosystems as well as on ecosystem functioning [1,2]. As a result, we face a double challenge: to improve our theoretical understanding of ecosystems and to use this improved knowledge cleverly. Can physics be of help in this major undertaking?
The increasing pressure on Earth’s resources and ecosystems means there is an urgent need to manage ecosystems more efficiently. So far, it is clear we have not succeeded, as exemplified by global warming and biodiversity loss [3,4]. To improve and diversify management options, we first need to improve our understanding of complex ecosystems in order to predict how they will change in response to different disturbances. With the exception of a few isolated cases, we are not yet capable of managing ecosystems as a whole. Experience has shown that we are still unable to predict the state of the ecosystems in which we have tried [5], for example, to reduce vegetation fragmentation [6], control invasive species [7], or modify geochemical fluxes [8] and intakes. Although it is true that “to predict is not to understand” [9], we hope a better understanding will help us predict, and ultimately manage ecosystems.
In this context, a wide body of literature addresses ecosystem issues with concepts and tools borrowed from physics along with more biological and socio-economic approaches. First, the ecologist community usually assumes that an ecosystem is a system which rigorously respects physical laws, and can thus be understood with concepts developed in physics. Physics is understood here as the natural science studying matter and energy in space and time. Matter and energy were probably the first physical variables proposed to tackle ecosystem functioning [10,11]. Conservation laws and thermodynamics provided the first concepts to apply these variables to ecosystem fluxes, and hence to grasp their global behaviours. In a way, species were ignored in such global (holistic) approaches, or rather they were considered as reservoirs of matter and energy which needed to be taken into account and controlled [12,13]. Here, I will not comment on physical tools such as the wide diversity of mathematical models successfully applied to ecological questions [14-17]. Rather, in the present survey, I focus on physical concepts only, and how relevant they are to understand ecosystems.
Based on physical concepts, ecologists soon discovered that ecosystems are open systems, while theories of physics (and thermodynamics) are more suitable for handling closed systems. Further, there is no clear homology (i.e. rigorous correspondence) between physical and ecological systems. One central reason for this observation soon became quite clear: ecosystems are not purely physical systems. The biological components of ecosystems (species) suppose that ecosystems behave differently from purely physical systems. In particular, species evolve by natural selection. This so-called duality problem of ecosystems led some authors including myself [18,19], to recommend looking for more generic and possibly radically new approaches than physical ones [20].
This is not to say that physics is of no use in ecology. On the contrary, it can be helpful, as in the past, when physics produced some highly generic and flexible concepts. For example, the information concept temporarily provided a powerful way to analyse ecosystems. Several informational attempts have been made to understand trophic processes and the components of biodiversity [21,22]. The analogy between information and thermodynamic entropy even offered a way to return to purely physical analyses. These approaches can be summarised under “statistical physics” and “extremal principle” concepts [13,23,24]. Here I will explore whether, today, we have gained sufficient distance to conclude that these approaches failed to help understand ecosystems [25,26].
Despite this possible failure, the long lasting collaboration between ecology and physics remains relevant, particularly to understand complex ecosystems. Some approaches which promote more universal concepts [20,27,28], represent new attractive ways to understand ecosystem functioning. Obviously, ecosystems have their specificities and difficulties. Ecosystems are constrained by physical as well as biological principles (the duality problem), which is combined with the boundary problem, i.e. it is difficult to define the boundaries of an ecosystem [18], the abstraction problem, the ecologist mentally and subjectively isolates the ecosystem under study, and the shortterm problem, the fact that an ecosystem lasts longer than human observations [19]. Yet, physics leads us to believe that it can sometimes avoid these research traps. There is no doubt that analysing past attempts and failures will help better exploit the interface between physics and ecology.
Ecology is a young science and is still searching for the most appropriate concepts to help understand ecological objects and processes [29]. The ecosystem is probably one of the most difficult object to study, as Tansley observed in an early definition [12]. The aim of this paper is not to list all the physical approaches used in ecology and to provide a definitive answer to the usefulness of physics in ecology. Rather I present past attempts to use physics in ecosystem ecology and give my personal view of the reasons for their partial failure. I want to emphasise that no survey of physical tools such as the wide body of differential equations and models applied to ecology will be found in this discussion paper. I hope to provide a basis for recommendations for the future use of physics in ecology, more specifically in ecosystem ecology. New concepts (or older concepts revisited in ecology) combined with powerful formalizations, seem to me to be fruitful way to analyse and manage ecosystems [17]. In particular, I will discuss how complexity, information and graph theory possibly open up new avenues to understanding ecosystems [20,28].
Challenges of Ecosystem Ecology
A great deal remains to be learned about ecosystems and how they function. The proof is our continuing inability to manage ecosystems despite recent improvements. We do know that the cyclic processes of transformation of matter and the circulation of energy largely determine the conditions which prevail in ecosystems [30,31]. These processes partly contribute to ecological services: regulating greenhouse gases, producing drinking water, or recycling waste, all contribute to ecosystem functioning [32-34]. How can we reconcile the many different and perhaps disparate elements of the system without trying to unify them in an integrated concept? We long believed that physical concepts such as energy or information could help integrate ecosystem processes and thus manage them for our benefit (and for that of the ecosystem).
While not pretending to be exhaustive, physics should be able to address at least four central ecosystem challenges. (i) While contributing to improving the human condition, the resulting changes have been responsible for increasing degradation of ecosystem services [32]. To imagine a sustainable future, in which we will manage our waste, and find food and energy in our environment is one of the greatest challenges facing ecosystem studies [1,34]. (ii) To ensure a sustainable future, the simplest precaution to take would be preserving the diversity of life. However, the functioning of the ecosystem is not only tied to its diversity and it is difficult to predict the behaviour of an entire ecosystem based on a small number of species because the presence of a few dominant species and their interactions can affect its key processes [16,31,35]. (iii) It is crucial to predict how ecosystems will react (or are already reacting) to climate change [36,37]. The capacity of ecosystems to respond is closely correlated with all their spatial, trophic, and genetic properties [20,38]. A lively debate is currently underway as to whether ecosystems could cross so-called tipping points, and thereafter undergo unpredictable regime shifts [39,40]. Lastly, (iv) the ecosystem is a complex system in that, among other reasons, the concept simultaneously embraces several levels of organisation [41,42]. Many scholars believe that this multiplicity of scales is largely responsible for our difficulty in understanding an ecosystem [43-46], and should be carefully addressed.
To sum up, any given ecosystem is made up of different components (biodiversity, human beings, and the atmosphere, at the least) and of a large number of dependent interactions (abiotic such as climatic interactions, biotic such as trophic interactions) over several scales, which make it extremely difficult to grasp [29,31,47]. Although this dual property is a basic tenet in ecology, it is rarely considered in practice. How can we coherently define such a multi-facetted object?
Early Concepts for Ecosystems
System dynamics
The first global view pioneer specialists had of an ecosystem was certainly that it was a cycle of matter [10,12]. Matter is here understood as any substance having a mass and filling a volume. The regulating role of nutrients in different ecosystems was reported very early on. Phosphorus, for example, is usually more limiting in freshwater systems, while nitrogen is more limiting in marine ecosystems [31,36]. Nitrogen and phosphorus are generated more rapidly by litter in tropical zones. The water and carbon cycles are well understood, and these cycles are now being discussed in depth in an effort to understand the roles and responses of ecosystems to ongoing global changes. Today, one may still wonder whether in a particular ecosystem, production is limited by a fluctuating supply of nutrients (ascending regulation) or by the species’ consumption of those nutrients (descending regulation) [11]. The two types of regulation are probably combined in varying proportions which are still not understood today.
On closer examination, viewing an ecosystem through its cycle of matter is not completely satisfactory. We know it is also important to understand how energy is distributed within the system [11,13]. Energy is here understood as the property of any object that may be used to perform a work or to heat the object. The auxiliary power supply ensures the exchange of matter, and appears to be essential for the functioning of the ecosystem. This energy, often of physical origin, allows the circulation of fluids which transport nutrients and biochemical elements. Typical examples are the circulation of water within plants due to evapotranspiration, and ascending currents (upwelling) in the oceans which supply the nutrients needed by organisms living just below the surface of the water [31,36]. The energy needed for plant growth and for the movement of living organisms is also a form of auxiliary energy.
Analyses of energy and matter transfers within an ecosystem highlighted the sizable losses of energy that occur from one trophic level to another during the predation/consumption process. According to pioneer studies, only 10% of energy passes from one level to a higher trophic level [11]. The rest is lost for the organisms at the bottom of the trophic chain, or even for all the species, in terms of calorimetric losses. This observation follows directly from the second law of thermodynamics, which states that energy conversion is always less than 100%. Losses may be due to energy degradation or dissipation. The second law of thermodynamics states that the spontaneous evolution of a closed system (i.e., a system which neither receives nor releases energy or matter) is accompanied by an increase in its entropy, in other words, in its “disorder”. Order can be increased (and, consequently, entropy locally reduced) only at the price of disorder, either equal or higher, otherwise introduced [48]. This remark also applies to open systems, including ecosystems. Clearly, any order that is locally imposed by, say, the trophic system’s constraints, can only exist at the price of a small increase in thermodynamic entropy at the level of the global system.
Thermodynamics and long term dynamics
Still, if any of the matter and energy studies are accurate, no ecosystem can be considered as a closed isolated system, like those sometimes encountered in physics. Even when an ecosystem has reached maturity (for example, when its functioning and its structure have stabilized), it continues to change and to respond to inputs, energy, and the species which enter it [13,23]. Its dynamics often resemble a self-regulating state of equilibrium, the state of an object understood here as having no net macroscopic flows of matter or of energy (through its boundary). However, one cannot ignore the permanent flows of energy, and those of matter, which maintain the structure of the ecosystem. The system itself is dissipative Glansdorff and Prigogine [48]: it makes the best use of the energy it receives, and consequently remains far from the state of thermodynamic balance (a state it would have reached if the system were actually closed). Thermodynamics is here understood as the branch of physics dealing with heat and temperature in relation to energy and work. Hence, the flow of energy allows the emergence of increasingly complex structures corresponding to a local reduction of entropy (the appearance of order, like in the trophic network). Despite this progress, the ecology of the past decades has admitted its inability to explain ecosystems with the help of thermodynamics.
In understanding ecosystem dynamics, knowing whether an ecosystem is close to equilibrium, or merely stable, is a major challenge for ecologists. Stability has several definitions. For our purposes, suffice it to say that an ecosystem is said to be stable if it can return to its previous state after an (unusual) disturbance [49,50]. When the system is dynamical, the stability of the state may be associated with the existence of an attractor or a basin of attraction. As we shall see below, the natural organisation of certain ecosystems may not fit such a clear-cut definition. While the variables describing a system are linked to certain constraints over time, as would be the case in an ecosystem, the state of the system does not move freely across all possible states. These states are displayed in the “phase space” defined by the variables describing the system. For example, its trajectory may be closed to form a cycle in this space, or even assume a chaotic shape called a “strange attractor” [51]. Yet, such chaotic behaviour has never been formally demonstrated for an ecosystem as a whole. When a disturbance or a catastrophe occurs, any system responds, and its trajectory in the phase space changes as a result or follows a specific potential surface [9]. Generally, an ecosystem is considered stable if its trajectory returns to its previous attractor or, which is equivalent, to a potential well [39,50]. The potential energy is here defined as the energy that possesses an object because of its position relative to other objects. This concept, which originates in the theory of dynamical systems, gives the impression that an ecosystem can be completely understood from the viewpoint of physics, even though it cannot.
The theory of dynamical systems has been applied in ecology, at least since pioneer studies on prey-predator systems [52,53]. Dynamical system is here understood as the science describing the behavior of complex systems. But in this case, the focus object of the dynamical system is usually not the ecosystem, but rather a reduced (biotic) part of it. Dynamical systems have enabled clarification of the wide range of species interactions in a supposedly fixed abiotic environment, whereas an ecosystem includes the environment as an essential component. This explains why I do not discuss species interactions from the perspective of dynamical systems in more detail here. There is no doubt that one day, dynamical systems will help better understand ecosystems, as dynamical system theory has only been partly explored in ecosystem ecology to date [39,54]. These are preliminary studies, and often concern a single component of the ecosystem (e.g., plant biomass). In addition, no rigorous analytical study has yet been conducted, i.e., with formal demonstrations, of system behaviours after detailed model calibration. Real progress will probably be achieved once a high-dimensional equation system succeeds in interconnecting the dynamics of a representative number of ecosystem components [55].
The dynamical approach is often said to be opposed to a more information-oriented point of view [38,56], but as we shall see, these viewpoints are not mutually exclusive. The following section details how the information concept was developed in physics, in parallel to dynamical system studies, and contributed to another physical view of ecosystems. We will then see whether this theoretically interesting attempt to understand ecological objects has succeeded or failed, so far.
Information theory
Information theory, conceived in the context of human communication [57], rapidly attracted the attention of ecologists. Information theory is here understood as the science studying the quantification, storage and communication of information content. Robert MacArthur, in particular, suggested quantifying the ecosystem energy flows studied by R. Lindeman, using a measure directly inspired by information theory [21]. According to this concept, the quantity of information conveyed by an event is inversely proportional to the a priori probability of the event occurring. It is intuitive that rare events carry more information than ordinary events, simply because they are unexpected. Information theory’s achievement was coming up with a way to quantify the information based on probability alone, regardless of the significance of the event. Using some key hypotheses, the theory proved that the average quantity of information of a class of events is minimal when all the events are equally likely. Many disciplines then made use of this theory.
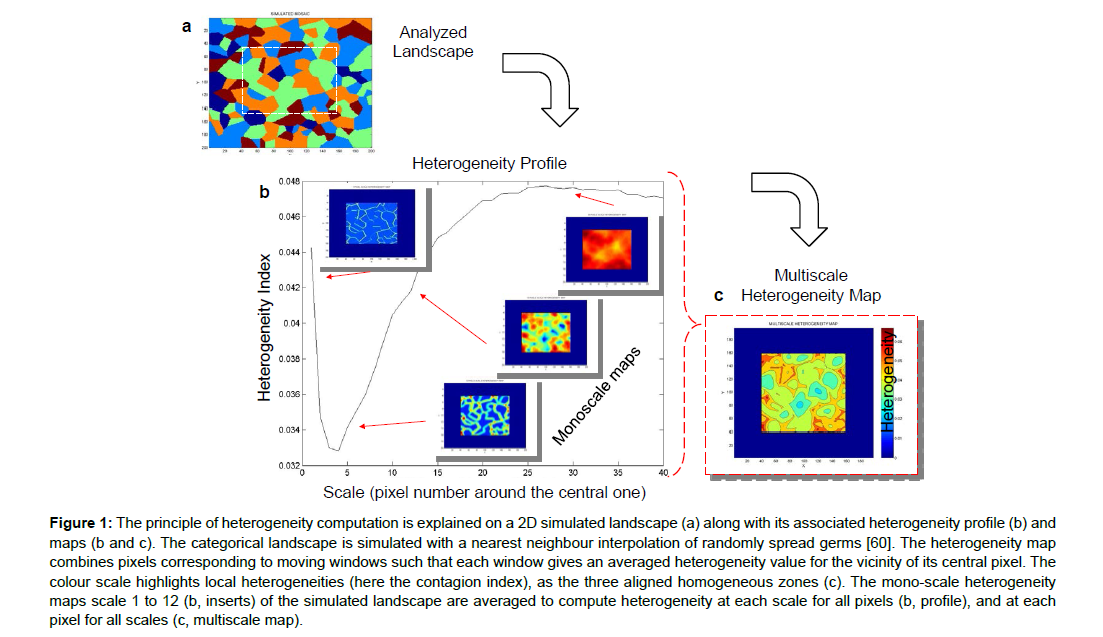
Later, landscape ecologists used it to quantify spatial structures, for example, the diversity of land covers (agricultural and other) using, among others, the Shannon index [58,59]. This index is highest when each patch considered, whatever its location, has the same probability of being covered with a forest, crop or any other type of vegetation. It thus measures a kind of disorder, diversity, and local heterogeneity (Figure 1). The index is highest (its sign has been changed in this ecological calculation) when different types of vegetation in neighbouring patches are grouped together. Conversely, several patches of a similar land cover provide a relatively homogeneous area, possibly at different spatial scales [60,61]. A plain in which cereals are grown, a closed area surrounded by hedges, or an agroforestry landscape will not have the same land cover characteristics, the same textural signature (Figure 1), and will therefore have different Shannon heterogeneity indices.
Figure 1: The principle of heterogeneity computation is explained on a 2D simulated landscape (a) along with its associated heterogeneity profile (b) and maps (b and c). The categorical landscape is simulated with a nearest neighbour interpolation of randomly spread germs [60]. The heterogeneity map combines pixels corresponding to moving windows such that each window gives an averaged heterogeneity value for the vicinity of its central pixel. The colour scale highlights local heterogeneities (here the contagion index), as the three aligned homogeneous zones (c). The mono-scale heterogeneity maps scale 1 to 12 (b, inserts) of the simulated landscape are averaged to compute heterogeneity at each scale for all pixels (b, profile), and at each pixel for all scales (c, multiscale map).
The information theory inadvertently drew an analogy between average information and entropy calculated from physical systems, two notions with the same formula. Entropy is here defined as the average amount of information produced by a stochastic source of data. The entropy of the information, the known information content of a system, logically contains data on the state of the system, the distribution of its constituents, identical (to a multiplicative constant) to that of thermodynamic entropy. This analogy has been the source of numerous misinterpretations in ecology (and elsewhere), as we shall see with the use of extremal principles [23,26], and is probably responsible for the majority of ecologists’ negative perception of thermodynamics.
Information entropy was behind the proposal to measure the state of a community of species based on the probability distribution of the flows of matter and energy in its associated trophic network [21]. Despite this step forward in quantifying a community of species, the suggested index has been found to be incomplete and difficult to measure. It does not account for transfer efficiencies (rates) between trophic levels. This deficiency led to the use of the same index, but based on existing populations rather than on the flows of matter or energy between them [22]. This approach has been reproduced several times, each time a little better than before. For example, it is important to be sure to not over-represent rare species which, because of their rarity, can carry more weight in the Shannon sense than is reasonable. Paradoxically, it is easier to estimate information content by concentrating on common species, since rare events are difficult to measure.
The Shannon index and other derivatives are widely used today for a rapid understanding of the structure of a community or a landscape [62,63], even though such indices have several potential traps. The first rule to observe in using such indices is to interpret the Shannon indexes among themselves, not as an absolute and self-explanatory value. To say that the (informational) entropy of a particular community is 50% lower than that of a neighbouring community means that the distribution of individuals is more even in the first community than in the second one for a comparable number of species.
This type of index can be useful to quantify the structure (Figure 1) and, to some extent, the dynamics of an ecosystem. In the maturation of an ecosystem, one would expect an increase in the number of species (strategies r towards K [21], and a reduction in their abundances, to reduce the total entropy of the system (taken as a whole), taking into account the number of species and species abundances. One might even be able to quantify the contribution of each species to total entropy, or the entropy between two species, in other words, to measure their degree of dependence [63,64]. For the first time, ecologists have a metric to measure the information within an ecosystem.
However, diversity indices derived from information theory have certain drawbacks. The first is an illusion of possible equivalence of information entropy (measuring the uncertainty in the system) and the diversity of the system. Indeed, several derived entropy indices quantify the same diversity differently. At the same time, a wide range of ecosystem structures can be characterised by the same information content. There is therefore no equivalence between information and species biodiversity in an ecosystem. Another hurdle is the dependence on the scale or organisational level at which the indices are calculated. The diversity of a community of insects is quite different when measured in one tree (which may also be considered as an ecosystem) or in the whole forest. It is usually preferable to compare diversity measurements made at the same level of organisation (e.g., organisms, populations, ecosystems…). As opposed to spatial and temporal scales which are continuous, levels of organization are discrete; they assume different processes and potentially highly different diversities. These indices involve many other problems related to sampling, as it is often difficult to isolate an individual for the purpose of adding it to (or subtracting it from) other individuals in the species or community concerned [62,65]. Therefore, diversity indices are sometimes calculated on the basis of genera, orders, or families of taxa within the communities of an ecosystem.
Failures of the Physical Concepts
Probabilistic views
More recently, ecologists discovered another major limitation of a diversity index based on probability, such as the Shannon index. Such an index has wide statistical variability: it is sensitive to rare species, which are harder to sample, and whose observation is subject to many hazards [62,66]. A diversity index of this sort presupposes that the species have equal weight and that the chances of observing them within the system are the same, which seems unlikely. Individuals of larger species have higher chances to be detected, and any probabilistic index seems to remain strongly biased. It would be relevant to estimate diversities at most (if not all) scales or at most organization levels of the ecosystem to grasp an unbiased view of the exact system diversity. The index also assumes that the states (or events, or categories) of the system are independent, with no correlations between them, without which the correlations would distort the probability of the occurrence of each state. A hypothesis like this would be illusory in a system as complex as an ecosystem. Indices are required that account for possible biases in estimation, such as q-entropies [67], which, although regularly mentioned, are rarely used in ecology [66].
Above, I stressed the impossibility of reducing an ecosystem either to its biocoenosis or to the community of species it hosts. This way of quantifying species diversity can provide an overview of the community, but not of the ecosystem. To consider a community of species in a fixed environment is also a strong approximation. This frequently implicit association must be made explicit if we wish to grasp the functioning of the system as a whole [20]. Nothing prevents us from quantifying the states of the ecosystem, instead of only those of its biocoenosis. Once we accept that biocoenosis should be included, the first difficulty is choosing the appropriate parameters which characterise the state of the ecosystem. In an ecosystem composed of flora, fauna, atmosphere, soil, and human populations - at the very least, we then need several descriptive parameters for each of these major components and their interactions [20,38]. Only then can we estimate the probability of the occurrence of their states, before calculating the diversity of the assemblage.
Grasping the ecosystem as a whole brings us closer to quantifying the complexity of the ecosystem. The Shannon index and its derivatives have another notorious weakness related to the synthetic characterisation of the complexity of an ecosystem. When applied to species distributions, this index is not sensitive to the order of the species: it is invariant in permutations. Even if the probabilities of the species were interchanged, the Shannon index value would remain unchanged. In the case of species, this advantage would be questionable if no species is presumed to play a particular role. Similarly, the invariance of a changed order has a lower value if we base the Shannon index on different types of land cover in a given landscape, as some of them may never reach certain probabilities [61,63]. A network of hedges, for example, can never fill the entire landscape, or they would no longer be hedges. Neither is such invariance suitable for application to a strongly oriented trophic network: from the primary consumers and decomposers to the species higher up in the trophic hierarchy, whose members are necessarily limited in number [11,68,69].
So, ecosystem complexity certainly masks a kind of order. It is instructive to compute an estimator which is sensitive to the shape of the probability distribution of the system constituents. For example, unlike the Shannon index, Fisher information can quantify the change in probabilities linked to a first approximation of the relative frequencies of their occurrence [70]. In a dynamic ecosystem, with a constant number of species, the probability of the presence of each species would nevertheless change over time. The gains and losses of information that an index like the Fisher index produces during ecosystem transitions are interesting to quantify, but they do not completely capture the complexity of the ecosystem. Both these indices are general, and convey little information about the organisation of the constituents. Fisher information cannot say if a sudden rise in certain probabilities is caused by bacteria or by grains of sand sticking to the trees (an abiotic process which could also alter the behaviour of the whole ecosystem). The notion of organisation or order is still missing. Instead, certain thermodynamic (extremal) principles may be useful to quantify the order underlying the organisation and dynamics of an ecosystem.
Extremal principles
In parallel with probabilistic attempts inspired by information theory, some ecologists explored the use of the analogy between information and (thermodynamic) entropy to characterise ecological systems. The notion of entropy still has good potential for ecological and biological systems. Extremal principles, here understood as any maximization or minimization of a state variable, are among several recent and therefore less known concepts which have tried to remedy theoretical drawbacks in ecology. The pioneering approach to species using information theory was modified to account for interactions among different species. Several indices which were originally informational, and later thermodynamic, have now emerged to account for the organisation of the species community.
For example, the ascendancy perspective relies on information shared among species, thus combining the correlations of the species among themselves [64]. Ascendancy quantifies the independence of populations from the presence of the others, for example, in terms of their respective abundances. Ascendency could be qualified as a measure of the uncertainty that can be observed indirectly in the network of relations among the species. This concept is closely related to the maturity of an ecosystem defined by Eugene Odum, and led to the hypothesis that one community of populations tends naturally to enhance its ascendancy, barring a disturbance [23,64]. In other words, steadily increasing amounts of information are needed to construct a complex and mature community, because the relations among the species become increasingly numerous and increasingly diversified over time.
The increase in a pure information index brings to mind a principle with which physicists are familiar: the principle of the maximization of thermodynamic entropy. The second law of thermodynamics states that during the transformation of energy within a closed system, part of the energy is lost in disorder (usually in the form of heat), and therefore cannot be converted back into work. This part of energy is quantified thanks to thermodynamic entropy, which can therefore be maximized [71]. In passing, it should be mentioned that the principle does not preclude a local reduction in entropy [72,73], as long as the entropy of the whole system remains maximized. The maximal disorder (or chaos) corresponds to the thermodynamic equilibrium of the system (i.e. a kind of stability in which the system has no net flows of matter or energy).
Unfortunately, a direct transposition of these physical results is not possible in the case of open systems, i.e., in the case of ecosystems which continually receive energy that maintains them far from thermodynamic equilibrium. It is known that such systems react to this energy input by degrading and dissipating the energy they receive [48]. While the complex relations among the components of the system emerge, the structures that dissipate the energy present in the system tend to organise themselves. They succeed partly through growth and reproduction within the system, and partly through exportation of matter and energy, such as animals migrating outside the ecosystem. However, the exact way ecosystems dissipate their workable energy remains a much-debated topic [26,73].
One may intuitively know that an undisturbed ecosystem tends to increase its organisation, that is, to locally and momentarily reduce its entropy. Faced with the failings of a purely thermodynamic approach, several ecologists tried to make use of different types of energy-related indices to recover this intuition. These indices are state-level variables which characterise an ecosystem subjected to an extremal principle, to various kinds of optimisation [23,25]. Among the pioneering works in this category are those on the maximization of the exergy rate [29,74].
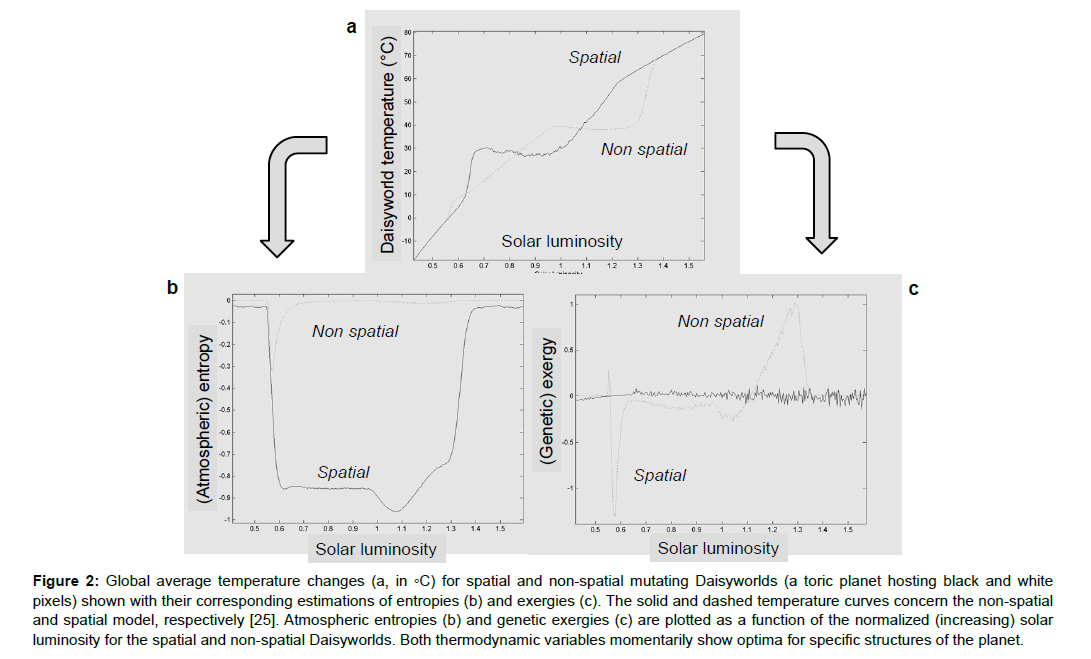
Exergy represents “usable energy” or work available for the system. This optimisation principle states that ecosystems tend to use all the means they possess to create dissipative structures (Figure 2). These means help degrade and break down the variations in energy (or gradients) intrinsic to the system, which helps dissipate the energy present. The maximization of the energy of an ecosystem (used by the organisms) is another way of tracing optimisation proposed by Howard Odum (Eugene’s brother) [13,24,71]. Similarly, the principle of maximum entropy production (Figure 2), which has occasionally been seen to be useful in biology, is less well established than the principle of maximization of entropy stating that the probability distribution which best represents the current state of knowledge of an object is the one with largest entropy, in statistical physics [25,73,75]. Extremal principles are still the subject of debate and have failed to dethrone information entropy from its intuitive role in ecology.
Figure 2: Global average temperature changes (a, in ◦C) for spatial and non-spatial mutating Daisyworlds (a toric planet hosting black and white pixels) shown with their corresponding estimations of entropies (b) and exergies (c). The solid and dashed temperature curves concern the non-spatial and spatial model, respectively [25]. Atmospheric entropies (b) and genetic exergies (c) are plotted as a function of the normalized (increasing) solar luminosity for the spatial and non-spatial Daisyworlds. Both thermodynamic variables momentarily show optima for specific structures of the planet.
To summarise, these continuing efforts concerning the principles of optimisation have proved to be ineffective for at least two reasons: first, it is not certain that an ecological system can be characterised by a purely physical and thus thermodynamic approach, and second, physics has not yet succeeded in correctly describing open systems that are out-of-equilibrium, like most ecosystems [38,76].
The failure of thermodynamics in ecology
When thermodynamics emerged as a science in the early 19th century, some scientists including Joseph Gay-Lussac and Sadi Carnot, were concerned with macroscopic variables such as the temperature, pressure, and entropy of a system. At that time, these variables were linked with the help of empirical laws. Fifty years later, Ludwig Boltzmann and Willard Gibbs succeeded in establishing a formal link of a statistical nature between the thermodynamic grandeurs of a system and the parameters of its microscopic constituents [72,77]. These developments helped put the concept of information on a proper footing, and paved the way for an informational interpretation of all physical systems.
Today we understand the links between the three major classes of physical system descriptions: a gas, for example, is generally considered as a continuous medium, or a statistical collection of particles, or even an assemblage of individual molecules in local interaction. In a macroscopic description (coarse scale), averaged quantities, such as temperature and density determined by hydrodynamic and thermodynamic equations, describe the behaviour of the gas. At the mesoscopic level (the level between the macroscopic and the microscopic levels), particles are grouped into classes according to their speeds and their positions, and we study the changes in their statistical distributions, that is, the set of their values. The microscopic approach (fine scale) considers gas as a complex system whose elements are theoretically discernible.
In physics, the conditions of transition from one level of modelling to another have not yet been formalised (e.g., [78]. The notion of macroscopic laws emerging through statistical aggregation from a finer level is a new idea that the ecologist community has embraced because of its great potential. Indeed, the living system structures may be viewed either as complex networks, as more regular and self-similar structures or as neutral (unbiased) structures too. In recent times, we have been attempting to describe the set of the constituents of an ecosystem or a community using a more or less neutral statistical distribution, with the aim of deducing their global behaviour. The task, which is more mathematical than truly physical, is arduous. By manipulating the individuals and the species instead of particles and energy levels, those engaged in these attempts hope to discover the abundance distribution in the observed elements or species of different ecosystems [27,73].
Even though the analogy with the gas particles appears to be intuitive, it is hard to work with for at least three reasons [38,76]: first, it presupposes a clear separation between the microscopic and the macroscopic states of the system (twenty or so orders of magnitude in physics, versus the three or four in ecology [79,80]; second, the definition of Shannon presupposes the independence of the constituents of the system (this may be obvious for particles, but is less so in the case of individuals linked with one another in a dense network of ecological interactions); and third, in order to be able to explain the maximization of information entropy, or of average energy, or of the average number of individuals per species, the relevant constraints which may have a bearing on them need to be defined beforehand. The transition from information entropy to thermodynamic entropy is thus not trivial.
The distribution of the populations of a species in a community is not the only aspect of the ecosystem one may wish to explain. From a biogeochemical point of view, the distribution of the chemical elements in an ecosystem, for example, is a property that holds information about the flow and quantity of the matter present. This field concerns stoichiometric distributions [30,81]. The distribution of matter inevitably influences the trajectory of the system over time. The method of entropy maximization applied here calls for a search for the most probable trajectory of the ecosystem [27,73] in the space defined by the concentrations of its chemical constituents and organisms. This probable trajectory is the one which corresponds to the largest number of ways of reaching the observed proportion of the constituents. As is the case with populations, this approach is purely combinatorial, and therefore statistical, except for the constraints chosen in the maximization (e.g., conservation of mass and/or energy). The system could thus be considered closed or not, depending on the point of view.
In brief, probabilistic views, extremal principles and thermodynamics all appear to have failed, so far, to provide efficient explanations for ecosystem functioning. What we need is not just the ability to measure information but to organise the information, the importance of which we already observed in system functioning. This constraint is quite close to the spirit of the algorithmic information theory, which is based on the notion of complexity. What we need is not just state variables to measure system states but a link between the description of the microscopic dynamics of a system (in our case, individuals, species, etc.) and the values of thermodynamic entities such as energy and entropy (in our case) which characterise the ecosystem.
Physics has not had Its Last Word
Statistical physics
Attempts to understand the biological and chemical components of ecosystems are purely physical in spirit. They provide the physical view that is complementary to the biological view of the briefly mentioned populational and evolutionary attempts to understand ecosystems. Yet, both the above-mentioned physical and biological approaches share the characteristic of being non-spatial. Space is usually implicit in them, that is, without any relationship being explicitly defined in terms of neighbourhood or constraints on displacements among the constituents of the ecosystem. Ecologists have long recognised the primordial role of spatiality in the functioning of the ecosystem [59,82]. The statistical physics, understood here as the branch of physics using probability theory and statistics to solve physical problems, approach can be modified to account for spatiality.
A model that readily comes to physicists’ minds is the Ising model, which was developed for ferromagnetic systems, i.e. materials that have acquired magnetization [83]. In the Ising model, the constituents are atoms given spins, magnetic moments that can point in two opposite directions. The new aspect of the Ising model is the fact that each atom influences the state of its neighbours and orients their spin in the direction of its own. The model predicts the probability of observing a certain spatial configuration for which the dominant spin will vary from one zone to another of the material. It also explains transitions between states in which long distance interactions emerge, as observed in other (living) systems [84]. Under certain conditions, the emerging spatial configuration is much simpler than might be expected from a statistical analysis.
The model was modified in the following decades to simulate soap lather, cell tissues, and other complex materials. Researchers looked for parameters analogous to the spin in the state of gas trapped in the soap bubbles or in the state of the cells of a tissue in contact with one another [85,86]. The constituents are then no longer atoms, but elements of another nature, bubbles or cells. These pioneer authors considered states which could take several values (and not just “high/up” or “low/ down” as for spin). They learned to characterise dynamic systems at the same time as how to modify the distribution of the states. The latest cell models even succeed in explaining the cellular adhesion observed in certain tissues [86].
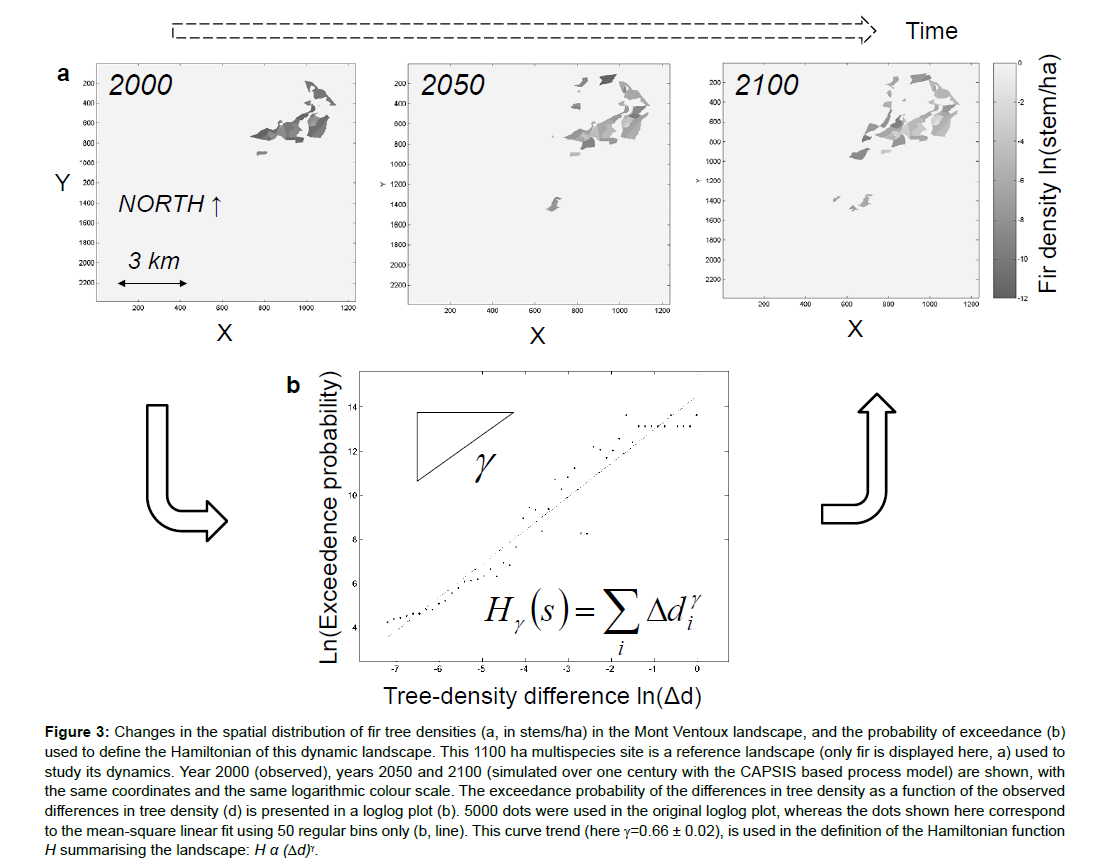
These approaches are based on the formalisation of a function which summarises the system and is named Hamiltonian. In statistical physics, we have long known that by minimizing this function, we can configure the state of the most probable system. In a previous paper [87], I proposed writing the Hamiltonian-like function of a forest ecosystem using an approach similar to that used in these previous works in physics and biology (Figure 3). This simple model, which remains phenomenological (non-mechanistic), accurately reproduces the distribution of the differences in tree densities between pairwise woodlots in an extended forest. This type of distribution is a spatial self-organisation characteristic of some forest landscapes.
Ising’s model and its extensions describe cases of self-organisation. The self-organisation concept, studied by Stuart Kauffman, Per Bak and their successors in the sciences of the living, corresponds to the spontaneous organisation of a system under the effect of the interactions of its constituents [46,88,89]. Self-organisation is usually observed when patterns emerge in a collective system formed by numerous elements of the same type [90]. Self-organisation is also involved during phase transitions in physics, for example, when snowflakes of various shapes appear close to 0°C. Self-organisation thus often manifests itself as the self-similarity (i.e., a structure that resembles its parts, as in fractal objects) of certain properties of the system. In the case of tree density, self-similarity may be found at the surface or in the borders between distinct states of a forest, or of grassland, etc. (Figure 3).
Figure 3: Changes in the spatial distribution of fir tree densities (a, in stems/ha) in the Mont Ventoux landscape, and the probability of exceedance (b) used to define the Hamiltonian of this dynamic landscape. This 1100 ha multispecies site is a reference landscape (only fir is displayed here, a) used to study its dynamics. Year 2000 (observed), years 2050 and 2100 (simulated over one century with the CAPSIS based process model) are shown, with the same coordinates and the same logarithmic colour scale. The exceedance probability of the differences in tree density as a function of the observed differences in tree density (d) is presented in a loglog plot (b). 5000 dots were used in the original loglog plot, whereas the dots shown here correspond to the mean-square linear fit using 50 regular bins only (b, line). This curve trend (here γ=0.66 ± 0.02), is used in the definition of the Hamiltonian function H summarising the landscape: H α (Δd)γ.
Self-similarity is a property which emerges due to local influences (e.g., the presence of a tree tends to favour the presence of a neighbouring tree). However, self-similarity is neither necessary nor sufficient for self-organisation, although many studies do not distinguish between them [91,92]. For example, the reaction–diffusion model proposed by Alan Turing in 1952, explains the organisation of regular spots that occur in the coats of certain animals or strips of vegetation without resulting in self-similarity [93]. Self-similarity has often been applied in ecology [14,79,80,90,91]. However, the approaches based on the selforganisation concept are still exploratory and rather phenomenological today. They are far from constituting proofs or explanatory theories.
There have been many attempts to interpret certain components of the ecosystem as resulting from self-organisation. These attempts concerned the distribution of the sizes of individuals in a community of species according to their metabolism [44,45], or the distribution of the number of species at a geological time scale (biotic), and even the preypredator relationships of ecosystems [94]. Concerning the abiotic part of ecosystems, the distribution of sub-watershed surfaces and a river network in a basin has also been shown [19,95]. Given these recent attempts, we would not be far from a general theory of ecosystems, but for the fact that they only pertain to certain components of the ecosystem. They are based on biocoenosis or on the biotope, only with evolutionary or energy considerations but, to my knowledge, never both at the same time. The link between these two dominant conceptual frameworks of the thermodynamic and biological (and evolutionary) ecosystem, remains to be established.
Complexity analyses
Is there a clear homology between physical and ecological systems that would allow the use of physical concepts (and tools) in ecology? If purely physical descriptions do not fit ecosystem functioning, should we shift slightly to other types (e.g. mathematical) concepts? From a physical concept, information rapidly became a more mathematical (that is, probabilistic and derived of its physical signification) concept which also appeared to be relevant in ecology. For example, it may be possible to quantify ecosystem complexity in terms of information. Complexity is here understood as the emergent behavior of any system whose components interact in multiple ways and follow local rules. But how can we measure information? What is information (and complexity) in ecology? Several information measures have been proposed in the past [38]. More recent measures, based on algorithmic and logical complexities, may reveal themselves to be fruitful in preliminary attempts.
Starting from the information (Shannon) theory [57], we have seen that some limits appear to be prohibitive. To base informational measures on probabilistic (or probabilistic distribution) principles is not sufficiently precise to grasp the presumed complexity of informational fluxes within an ecosystem. In particular, the ordering (organisation) of information, which appears to be crucial to the functioning of the system, also needs to be carefully quantified. The organisation constraint is the motivation for the algorithmic information theory. The Kolmogorov- Solomonov algorithmic complexity grasps part of the inner ordering of the data [96,97]. The algorithmic complexity suggests quantifying the complexity of a system (object) using the shortest program that could re-create it. Such a definition of complexity requires a specific model of data organisation, of regularities, symmetry, alignment and/or pooling. Indeed, the lack of specific regularity in data would prevent them from being shortened efficiently. This measure has only occasionally been applied to ecosystems [19], partly because the shortest program needed is practically unreachable.
This measure appears not to be in perfect agreement with our intuitive perception of complexity. Indeed, algorithmic complexity describes random data as highly complex, as they are almost impossible to shorten into a condensed program to (re)produce them [96,97]. Other complexity measures were then proposed to avoid this limitation. For example, logical depth measures the complexity of an object by the time needed to execute this shortest program to reproduce the object [98,99]. The difference between algorithmic complexity and logical depth is subtle but, for the first time, makes it possible to take the history of the object, i.e. the time needed to build the complex system, in account. It does not only consider the state of the system or object at a specific date. Yet, logical depth remains a theoretical concept and is still rarely used in concrete examples of complexity quantification [98]. In this line of thought, I have proposed a way to apply this concept to ecosystem quantification [19], although it is not sure that this kind of complexity will fit requirements for the quantification of complexity and information in ecology. It remains a global and fixed picture of the (eco)system, in which the inner functioning of the system under study is still missing.
In conclusion, it seems that ecosystem information is not accessible. To understand this, let us assume that we dispose of flexible and efficient means to measure the complexity and/or information of a system or an object. Although it would be almost if not entirely impossible to measure all parts of the system, we would still need to concretely apply it to an “ecosystem quantification”. One way I proposed is to build a numerical model of the ecosystem that is as realistic as possible, (e.g., after careful calibration and validation using observed systems), and to then quantify the model instead of the real system [19,99]. Any kind of ecosystem model may be appropriate here, although more exhaustive and more integrated models are highly recommended here. Like every model, the ecosystem model will be a pale copy of the real ecosystem, but one may hope it will mimic the object concerned with sufficient accuracy to reproduce its functioning and successive changes. With such a model, it would be possible to dissect the different processes involved in the functioning of the whole and to measure the information stores and fluxes it hosts separately.
Graph analyses
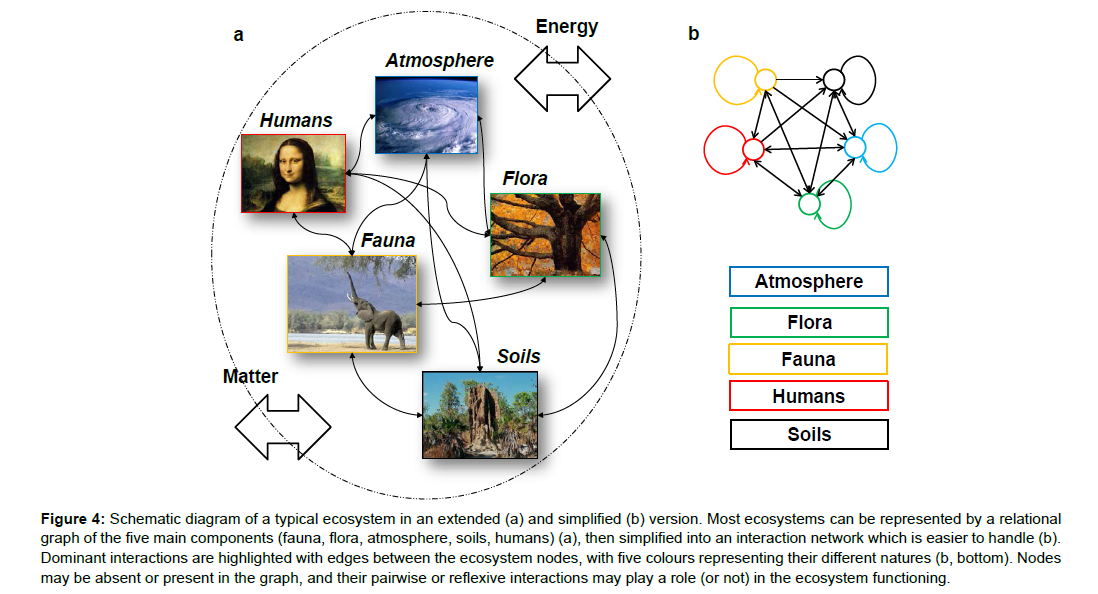
A wide range of other physical (and mathematical) concepts can certainly be borrowed by ecology. One concept which is currently attracting increasing attention is the graph concept, inspired by graph theory [100,101]. Graph theory is here understood as the area of mathematics which studies pairwise relations between objects (and thus displaying graph structures). To apply the graph concept in ecosystem ecology involves choosing certain ecosystem constituents, defining them as nodes, linking them by a set of edges wherever they interact, and then studying the (simplified) graphic representation of this ecosystem (Figure 4). For example, a graph can be used to represent the topological structure of a community of species, and the dynamics of their interactions [11,28,102].
Figure 4: Schematic diagram of a typical ecosystem in an extended (a) and simplified (b) version. Most ecosystems can be represented by a relational graph of the five main components (fauna, flora, atmosphere, soils, humans) (a), then simplified into an interaction network which is easier to handle (b). Dominant interactions are highlighted with edges between the ecosystem nodes, with five colours representing their different natures (b, bottom). Nodes may be absent or present in the graph, and their pairwise or reflexive interactions may play a role (or not) in the ecosystem functioning.
When applied to trophic (i.e. feeding) or non-trophic interaction networks, this approach has enabled fruitful studies. Any network is inherently modelled as a graph, and mutualistic communities and plant-pollinator systems are among the many networks of species’ interactions which have been successfully studied using cutting-edge, network-based models [20,28,103]. However, these models have been found to overlook abiotic interactions, or to reduce them to the status of simple external input-output interactions. A more balanced view between biotic and abiotic components is required, in practice, and is accessible today [20].
In the spatial domain too, a wide range of land cover mosaics can be represented by a graph, and their structural and connectivity properties have been studied in landscape ecology. Such studies, which, in a sense, combine interacting ecosystems in the same landscape, have been conducted in both marine and terrestrial landscapes [60,63]. This intuitive way of summarising the connectivity of space appears to be sufficiently powerful to understand the fluxes of matter and organisms in any kind of mosaic. Yet, here again, a graphic representation does not appear to be the best way to understand landscape functioning, because graphs favour structural rather than functional analyses [104]. While it is perfectly possible to capture function and processes in a specific graph, so far, in ecology, graphs have remained frozen, and at best compared with each other in a diachronic analysis. Studies of changing graphs, for instance to grasp the appearance/disappearance of species or landscape elements remain rare [20,105,106], partly due to lacking data over the long term. This emphasises the need for more functional modelling, and not only frozen analyses, in ecological graphs.
Discussion
The ecosystem: a physical system or a biological system?
We have seen that a conceptual problem rapidly arises in the study of ecosystems. Ecosystems are a combination of, say, at least five components of highly different nature: flora, fauna, soils, the atmosphere, and human components. Furthermore, these components partly belong to living (called “biotic”) and non-living (“abiotic”) domains and interact at different scales. Hence, ecosystems are a priori simultaneously. constrained by biological and physical laws, including natural selection and thermodynamics [18,19,46]. This observation suffices to explain why, so far, each component has been studied separately or in pairwise interactions, focusing on either the physical or biological processes at stake. In a sense, this kind of “third state” of the matter, between purely physical and purely biological natures, makes them difficult to understand [12]. The present definition is still unable to include all the complexity of observed ecosystems, and in particular human related processes [1,2].
Facing the physical view in ecology, biologists are sensitive to both the trophic and non-trophic interactions which occur in ecosystems, to the spatial distribution of the biotic (living) communities, and to their collective genotype. These properties are rather complex, and their dynamic articulation remains to be investigated in depth [105,106]. The living component of the ecosystem is a full-fledged biological system. It follows the rules of evolution, with a more or less gradual change in the species it hosts in the long term. Since Darwin, it has been shown that evolution is the result of random mutations of genomes under selection pressures which often occur in the environment [107]. A piece of genetic information which enables organisms to better adapt to their environment has a better chance of being transmitted to following generations, and therefore of being retained. Broadly speaking, the same goes for higher level of assemblages such as ecosystems, all of which are made up of genomes [38,107,108].
Early models only tackled the biotic components of the ecosystem, and thus defined the ecosystem as a community of different interacting species. Lotka and Volterra [109] built a demographic model of two or more species in prey-predation interaction [109]. However, at broader organisational levels (and scales), the trophic network can be studied as a whole [47], providing concepts such as trophic dynamics, which are often linked to the topological structure of the trophic network [103]. Other networks of species interactions have also been studied including mutualistic communities and plant-pollinator systems, more recently with cutting-edge network-based models [20,28].
An ecosystem is neither a strictly physical nor a strictly biological system [69]. It is a hybrid system consisting of elements that require the intertwining of two descriptions, one with a basis in thermodynamics, the other in natural selection. Why not build a third description? I do not subscribe to the notion endorsed in certain studies that, for the sake of simplicity, the ecosystem is reduced to its biotope or to its biocoenosis. These two views, either a species centred view or a matter-and-energy view, have long been the subject of debate in ecology [13,21,46]. It is time to merge these two views into more integrated views and models. This implies accounting for the widest range of processes, of different natures including individual interactions, physical fluxes, and spatial relationships, among others [20,31]. This also implies including populations (i.e., organisms) as well as physical entities (concentrations of gases and chemical elements) with similar weights in the same model [55], not only one occasionally disturbing the other one. The question is: are physical concepts still able to reconcile these different points of views?
What next?
In conclusion, I have reviewed some landmark physical concepts and theories used in ecology, and described how they helped advance our understanding of ecosystem functioning. I do not claim this list is exhaustive, as other review papers partly covered this issue [14,17,22,23], but it suffices to provide a conceptual link between physical frameworks and ecosystem ecology. Here, I also wish to emphasise that discussing the use of physical tools (e.g. differential equations) and models is beyond the scope of this paper. Here follows a short list of points summarising the main conclusions of this article:
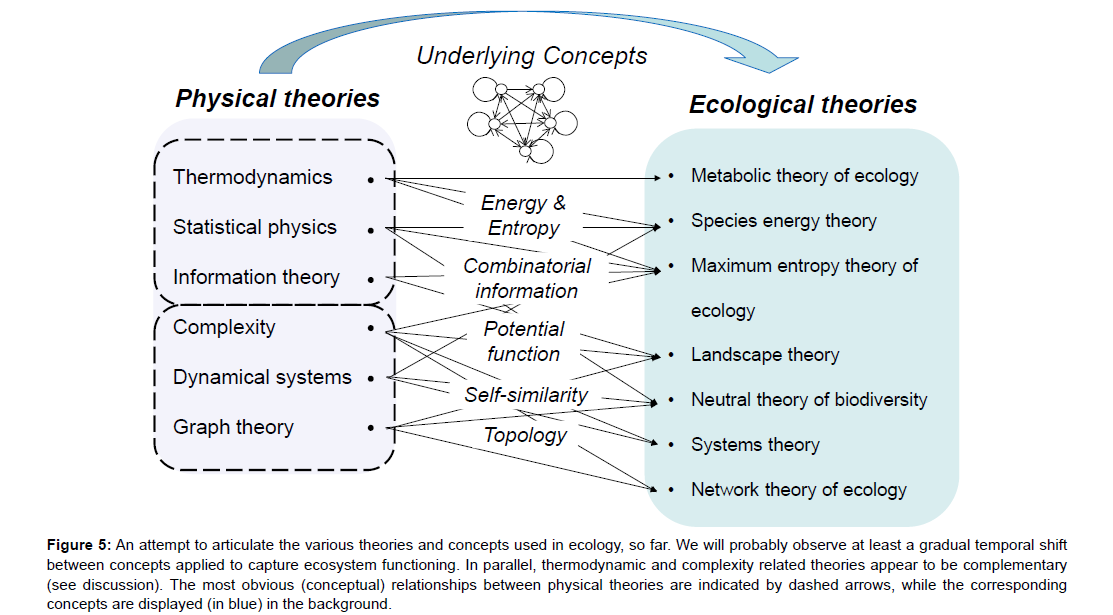
• I have identified a first set of physical theories and concepts applied to ecosystem ecology, namely thermodynamics, statistical physics and information theory, by way of energy, combinatorial information and entropy (possibly mixed) concepts (Figure 5). These theories are historically linked and are still used for ecological applications, often related to ecosystems. Today, ecologists may conclude that the failure to apply this set of theories to the ecosystem as a whole was only temporary [29,38]. The apparent similarities between informational, physical and combinatorial entropies led us to hope that these concepts could also be applied to ecological systems, and would lead to a deeper understanding [21,22,59]. But they did not.
Figure 5: An attempt to articulate the various theories and concepts used in ecology, so far. We will probably observe at least a gradual temporal shift between concepts applied to capture ecosystem functioning. In parallel, thermodynamic and complexity related theories appear to be complementary (see discussion). The most obvious (conceptual) relationships between physical theories are indicated by dashed arrows, while the corresponding concepts are displayed (in blue) in the background.
• This does not mean that some ecological processes, as parts of ecosystem functioning, have not been finely understood with the help of physics. Nor should it be concluded that physical approaches will not lead to other fascinating discoveries in the science of ecology in the future. One possible track in this direction pertains to complexityrelated theories (Figure 5). In this review, I have tried to show how the iterative (self-similar) and non-linear processes underlying ecosystem dynamics illustrate relationships between self-organisation, dynamical systems and complexity theory [46]. Another potentially interesting concept related to complexity approaches concerns the topology or graph-oriented representation of ecosystems [19,28,68]. Will this recent application of a physical-like concept succeed where entropy and information concepts failed?
• Despite long lasting efforts, physics alone will probably not suffice to explain ecosystem functioning. The reason is now beginning to emerge: ecosystems are simultaneously physical and biological systems [18,19,29]. For the same reason, ecosystems will likely not be understood using purely biological and evolutionary approaches (not detailed in this paper). Consequently, we have the responsibility of finding a way to encompass this duality. Is physics combined with biology more likely to succeed? My intuition and that of some of my colleagues suggests that we should rather look for radically new ways of analysing this specific state of matter [20,38,55]. How to proceed?
• One way would be to look for some more generic concepts and more versatile tools to be used with ecological entities of different natures. Future notions should encompass entities that are as different as physicochemical, biological and human components (and processes). Today, many ecologists believe that information, graph or complexity concepts could help to achieve this multi-purpose objective (Figure 5). At the same time as identifying such generic concepts, we should develop a set of tools to handle and test them on observed ecosystems to answer the following questions. How should ecosystem information be handled? How can ecosystem complexity be quantified? Combining pattern- and process-oriented approaches will definitely help grasp ecosystem (structural) properties as the same time as ecosystem functioning.
• Ecosystems embed a large number of interdependent interactions which need to be disentangled to enable precise understanding [20,31,46]. To analyse a state or even several states of the ecosystem is rather like analysing a person only using photographs: it provides an incomplete, instant but ultimately erroneous view of the person. Today we need to invest in more functional, dynamical and integrated analyses of ecosystems. For example, to represent an ecosystem with a graph is a useful preliminary step, but to combine the fluxes of matter and energy simultaneously to a changing topology is likely the next necessary step [20,39,110]. Work towards achieving this objective has already begun, although integrated models of the ecosystem are still rare [20,28,105]. The duality problem falsely suggests analysing either certain biotic (e.g., species community) or abiotic (e.g., environmental factors) components of the ecosystem, thereby reducing the study of the other parts to negligible components.
A book would not suffice to explore all the links between physics and ecology, even though such an in-depth survey would likely benefit reflection on the successes and failures of ecosystem ecology. Many difficulties face ecologists who are trying to understand and manage ecosystems today. I intentionally avoided some debates such as the issue of ecosystem boundaries [18]. Neither did I mention what in another study, I called the “short-term view” we, as humans, have of ecosystems and their probable long-term development [20]. Indeed, some pioneer works already observed the highly changeable components of ecosystems [13,21]: continuously hosting new species and acquiring new area, losing some communities and some genomes, ecosystems undergo long term “development” (i.e., structural changes) close to those about the organismic nature of the ecosystem, which were the subject of long debate. In turn, these changes in composition have a direct impact on changes in properties and behaviour [111,112].
Today, there is no doubt that ecosystems are objects with specific and critical history, sometimes exhibiting sharp changes in the long term. For all these reasons, we need to build innovative and generic concepts to understand them. This is one of the main challenges facing ecology today.
References
- Cincotta RP, Wisnewski J, Engelman R (2000) Human population in the biodiversity hotspots. Nature 404: 990-992.
- Butler SJ, Vickery JA, Norris K (2007) Farmland biodiversity and the footprint of agriculture. Science 315: 381-384.
- IPCC (2007) Climate change 2007. Cambridge University Press, Cambridge, UK.
- Kolbert E (2014) The Sixth Extinction: An Unnatural History. Henry Holt & Company.
- Mouquet N, Lagadeuc Y, Devictor V, Doyen L, Duputié A, et al. (2015) Predictive ecology in a changing world. J Applied Ecol 52: 1293-1310.
- Bascompte J, Sole RV (1996) Habitat Fragmentation and Extinction Thresholds in Spatially Explicit Models. J Anim Ecol 65: 465-473.
- Bermann M, Andersen A, Hély C, Gaucherel C (2013) Overview of the Distribution, Habitat Association and Impact of Exotic Ants on Native Ant Communities in New Caledonia. PLoS ONE 8.
- West TO, Marland G (2002) Net carbon flux from agricultural ecosystems: methodology for full carbon cycle analyses. Environ Pollut 16: 439-444.
- Thom R (1975) Structural stability and morphogenesis: An Outline of a General Theory of Models. Benjamin, Reading, MA.
- Â Proulx R (1942) The trophic-dynamic aspect of ecology. Ecology 23: 399-417.
- Tansley A (1935) The use and abuse of vegetational concepts and terms. Ecology 16: 284-307.
- Odum EP (1971) Fundamentals of ecology. (3rd edn.), Saunders, Philadelphia, US.
- Harte J (2004) The value of null theories in ecology. Ecology 85: 1792-1794.
- Tilman D, Reich PB, Knops JMH (2006) Biodiversity and ecosystem stability in a decade-long grassland experiment. Nature 441: 629-632.
- Loreau M (2010) The Challenges of Biodiversity Science. International Ecology Institute, Oldendorf/Luhe, Germany.
- Marquet PA, Allen AP, Brown JH, Dunne JA, Enquist BJ, et al. (2014) On Theory in Ecology. BioScience 64: 701-710.
- Gignoux J, Davies ID, Flint SR, Zucker JD (2011) The ecosystem in practice : interest and problems of an old definition for constructing ecological models. Ecosystems 14: 1039-1054.
- Gaucherel C, Salomon L (2014) A neutral model as a null hypothesis test for river network sinuosity. Geomorphology 214: 416-422.
- Gaucherel C, Théro H, Puiseux A, Bonhomme V (2017) Understand ecosystem regime shifts by modelling ecosystem development using Boolean networks. Ecol Complex 31: 104-114.
- MacArthur RH, Wilson EO (1963) An Equilibrium theory of insular zoogeography. Evolution 17: 373-387.
- Margalef R (1968) Perspectives in ecological theory. University of Chicago Press, Chicago.
- Patten BC (1995) Network Integration of Ecological Extremal Principles - Exergy, Emergy, Power, Ascendancy, and Indirect Effects. Ecol Modell 79: 75-84.
- Jorgensen SE (1999) State-of-the-art of ecological modelling with emphasis on development of structural dynamic models. Ecol Modell 120: 75-96.
- Gaucherel C (2006) Influence of spatial structures on ecological applications of extremal principles. Ecol Modell 193: 531-542.
- Haegeman B, Loreau M (2008) Limitations of entropy maximization in ecology. Oikos 117: 1700-1710.
- Neill C, Gignoux J (2008) Prediction of non-equilibrium dynamics in ecosystems : from dogs and fleas to molecules and organisms. Journal of Statistical Mechanics: Theory and Experiment.
- Campbell C, Yang S, Albert R, Sheab K (2011) A network model for plant-pollinator community assembly. Proceedings of the National Academy of Sciences (PNAS) 108: 197-202.
- Schwartz A, Jax K (2011) Ecology revisited. Reflecting on Concepts, Advancing Science. Springer, Dordrecht, Heidelberg, London, New York.
- Sterner RW, Elser JJ, Hessen DO (1992) Stoichiometric relationships among producers, consumers and nutrient cycling in pelagic ecosystems. Biogeochem 17: 49-67.
- Costanza R, d'Arge R, de Groot R, Farber S, Grasso M, et al. (1997) The value of the world's ecosystem services and natural capital. Nature 387: 253-260.
- Costanza R, Voinov A, Boumans R, Maxwell T, Villa F, et al. (2002) Integrated ecological economic modeling of the Patuxent River watershed, Maryland. Ecol Monograph 72: 203-231.
- MEA (2005) Current state and trends assessment. Island Press, Washington D.C, USA.
- Naeem S (2002) Ecosystem consequences of biodiversity loss: The evolution of a paradigm. Ecology 83: 1537-1552.
- Stenseth NC, Mysterud A, Ottersen G, Hurrell JW, Chan KS, et al. (2002) Ecological effects of climate fluctuations. Science 297: 1292-1296.
- Walther GR, Post E, Convey P, Menzel A, Parmesan C, et al. (2002) Ecological responses to recent climate change. Nature 416: 389-395.
- Dessalles JL, Gaucherel C, Gouyon PH (2016) The thread of life. The immaterial face of Nature.
- Scheffer M, Carpenter S, Foley JA, Folke C, Walker B (2001) Catastrophic shifts in ecosystems. Nature 413: 591-596.
- Brook BW, Ellis EC, Perring MP, Mackay AW, Blomqvist L (2013) Does the terrestrial biosphere have planetary tipping points. Trends Ecol Evol 28: 396-401.
- Allen TFH, Starr TB (1982) Hierarchy: perspectives for ecological complexity. University Chicago Press, Chicago, US.
- O'Neill RV, De Angelis DL, Waide JB, Allen THF (1986) A hierarchical concept of ecosystems. Trends Ecol Evol 2: 26-27.
- West G, Brown J, Enquist B (1997) A general model for the origin of allometric scaling laws in biology. Science 276: 122-126.
- Brown JH, Gupta VK, Li BL, Milne BT, Restrepo C, et al. (2002) The fractal nature of nature: power laws, ecological complexity and biodiversity. Philosophical Transactions of the Royal Society of London Series B-Biological Sciences 357: 619-626.
- Solé RV, Bascompte (2006) Self-Organization in Complex Ecosystems. Princeton University Press, Princeton, pp. 384.
- Johnson KH (2000) Trophic-dynamic considerations in relating species diversity to ecosystem resilience. Biol Rev Camb Philos Soc 75: 347-376.
- Glansdorff P, Prigogine I (1971) Thermodynamic theory of structure, stability and fluctuations. Science 176: 1410.
- Holling CS (1973) Resilience and stability of ecological systems. Ann Rev Ecol Syst 4: 1-23.
- Walker B, Holling CS, Carpenter S, Kinzig A (2004) Resilience, Adaptability and Transformability in Social-ecological Systems. Ecology and Society 9.
- Lorenz EN (1963) Deterministic Nonperiodic Flow. J Atmos Sci 20: 130-141.
- Volterra V (1926) Fluctuations in the abundance of a species considered mathematically. Nature 188: 558-560.
- May R (1976) Simple mathematical models with very complicated dynamics. Nature 261: 459-467.
- Carpenter SR, Cole JJ, Pace ML, Batt R, Brock WA, et al. (2011) Early Warnings of Regime Shifts: A Whole-Ecosystem Experiment. Science 332: 1079-1082.
- Hély C, Shuggart HH, Swap B, Gaucherel C (2018) The Drape Concept to Understand Ecosystem Dynamics and its Tipping Points.
- Noble D (2008) The Music of Life: Biology Beyond Genes. Oxford University Press, p: 153.
- Shannon CE, Weaver W (1949) The mathematical theory of communication. The University of Illinois Press, Urbana, Illinois, USA.
- Forman RTT, Godron M (1986) Landscape ecology. John Wiley and Sons, New York.
- Turner MG, Gardner RH (1991) Quantitative methods in landscape ecology. Springer Verlag, New York.
- Gaucherel C, Burel F, Baudry J (2007) Multiscale and Surface pattern analysis of the effect of landscape organisation on carabid beetles distribution. Ecol Indic 7: 598-609.
- Gaucherel C (2010) Self-similar land cover heterogeneity of temperate and tropical landscapes. Ecol Complex 6: 346-352.
- Hubbell S (2001) The unified neutral theory of biodiversity and biogeography. Princeton University press, Princeton, p: 392.
- Burel F, Baudry J, Ghersa CM, Poggio SL (2003) Landscape ecology: concepts, methods, and applications. Science Publishers, Enfield.
- Ulanowicz RE (2001) Information theory in ecology. Computers & Chemistry 25: 393-399.
- Levin SA (1992) The problem of pattern and scale in ecology. Ecology 73: 1943-1967.
- Rényi A (1961) On measures of information and entropy. Berkeley Symp on Math Statist and Prob 1: 547-561.
- Proulx SR, Promislow DEL, Phillips PC (2005) Network thinking in ecology and evolution. Trends Ecol Evol 20: 345-353.
- Akkerhuis JOGA (2008) Analysing hierarchy in the organization of biological and physical systems. Biol Rev Camb Philos Soc 83: 1-12.
- Fath BD, Cabezas H (2004) Exergy and Fisher Information as ecological indices. Ecol Modell 174: 25-35.
- Milewski AV, Mills AJ (2010) Does life consistently maximise energy intensity. Biological Reviews 85: 859-879.
- Prigogine I, Nicolis G (1977) Self-Organization in Non-Equilibrium Systems: Towards A Dynamics of Complexity. Bifurcation Analysis pp. 3-12.
- Dewar RC, Lineweaver CH, Niven RK, Regenauer-Lieb K (2011) Beyond the Second Law. Entropy Production and Non-equilibrium Systems. Springer.
- Schneider ED, Kay JJ (1994) Life as a manifestation of the second law of thermodynamics. Math Comput Modelling 19: 25-48.
- Gaucherel C (2014) Ecosystem Complexity through the Lens of Logical Depth: Capturing Ecosystem Individuality. Biol Theory 9: 440-451.
- Golse F, Saint-Raymond L (2004) The Navier-Stokes limit of the Boltzmann equation for bounded collision kernels. Inventiones mathematicae 155: 81-161.
- Seuront L, Schmitt F, Schertzer D, Lagadeuc Y, Lovejoy S (1996) Multifractal intermittency of Eulerian and Lagrangian turbulence of ocean temperature and plankton fields. Nonlin Processes Geophys 3: 236-246.
- Scanlon TM, Caylor KK, Levin SA, Rodriguez-Iturbe I (2007) Positive feedbacks promote power-law clustering of Kalahari vegetation. Nature 449: 209-212.
- Daufresne T (2013) Palaeoecology: Megafauna as a nutrient pump. Nat Geosci 6: 679-680.
- Forman RTT, Godron M (1981) Patches and structural components for a landscape ecology. BioScience 31: 733-740.
- Ising E (1925) Contribution to the theory of ferromagnetism. Z Phys 31: 253-258.
- Potts RB (1952) Some generalized order-disorder transformations. Proceedings of the Cambridge Philosophical Society 48: 106-109.
- Glazier JA, Balter A, Poplawski NJ (2007) Magnetisation to morphogenesis: A brief history of the Glazier-Graner-Hogeweg Model. In Anderson ARA, Chaplain MAJ, Rejniak KA editors. Single-cell based models in biology and medicine. pp. 79-106.
- Gaucherel C (2010) Self-organization of patchy landscapes: Hidden optimization of ecological processes. J Ecosys Ecograph 1.
- Kauffman SA (1969) Metabolic stability and epigenesis in randomly constructed genetic nets. J Theor Biol 22: 437-467.
- Jensen HJ (1998) Self-Organized Criticality: Emergent Complex Behaviour in Physical and Biological Systems. Cambridge, University Press, Cambridge.
- Gisiger T (2001) Scale invariance in biology: coincidence or footprint of a universal mechanism. Biol Rev Camb Philos Soc 76: 161-209.
- Rietkerk M, Boerlijst MC, van Langevelde F, HilleRisLambers R, van de Koppel J, et al. (2002) Self-organization of vegetation in arid ecosystems. Am Nat 160: 524-530.
- Kefi S, Rietkerk M, Alados CL, Pueyo Y, Papanastasis VP, et al. (2007) Spatial vegetation patterns and imminent desertification in Mediterranean arid ecosystems. Nature 449: 213-217.
- Lefever R, Lejeune O (1997) On the origin of tiger bush. Bull Math Biol 59: 263-294.
- Hatton IA, McCann KS, Fryxell JM, Davies TJ, Smerlak M, et al. (2015) The predator-prey power law: Biomass scaling across terrestrial and aquatic biomes. Science 349.
- Rodriguez-Iturbe I, Rinaldo A (1997) Fractal River Basins: Chance and Self-Organization. Cambridge University Press, New York, USA.
- Kolmogorov AN (1965) Three approaches to the quantitative definition of information. Int J Comput Math 2: 157-168.
- Delahaye JP (2006) Complexities: The limits of mathematics and computer science. Pour la science, Paris, France.
- Bennett CH (1988) Logical depth and physical complexity. In Herken R editor. The universal Turing machine: a half-century survey. Oxford University Press, Oxford. pp: 227-257.
- Zenil H, Delahaye JP, Gaucherel C (2011) Image characterization and classification by physical complexity. Computational Complexity, p: 30.
- Barabási AL, Albert R (1999) Emergence of scaling in random networks. Science 286: 509-512.
- Fontaine C, Guimaraes PR, Kéfi S, Loeuille N, Memmott J, et al. (2011) The ecological and evolutionary implications of merging different types of networks. Ecol Lett 14: 1170-1181.
- Montoya JM, Solé RV (2002) Small world patterns in food webs. J Theor Biol 214: 405-412.
- Foltête JC, Giraudoux P (2012) A graph-based approach to investigating the influence of the landscape on population spread processes. Ecol Indic 18: 684-692.
- Loreau M, Naeem S, Inchausti P, Bengtsson J, Grime JP, et al. (2001) Biodiversity and ecosystem functioning: current knowledge and future challenges. Science 294: 804-808.
- Webb CO, Ackerly DD, McPeek MA, Donoghue MJ (2002) Phylogenies and community ecology. Ann Rev Ecol Syst 33: 475-505.
- Gliddon CJ, Gouyon PH (1989) The units of selection. Trends Ecol Evol 4: 204-208.
- Swenson W, Wilson DS, Elias R (2000) Artificial ecosystem selection. Proceedings of the National Academy of Sciences (PNAS) 97: 9110-9114.
- Wangersky PJ (1978) Lotka-Volterra population models. Ann Rev Ecol Syst 9: 189-218.
- Sayama H, Laramee C (2009) Generative Network Automata: A Generalized Framework for Modeling Adaptive Network Dynamics Using Graph Rewritings. In Gross T, Sayama H editors. Adaptive Networks. Theory, models and applications, pp. 311-332.
- Gaucherel C, Boudon F, Houet T, Castets M, Godin C (2012) Understanding Patchy Landscape Dynamics: Towards a Landscape Language. PLoS ONE.
- May RM (1973) Qualitative Stability in Model Ecosystems. Ecology 54: 638-641.
Citation: Gaucherel C (2018) Physical Concepts and Ecosystem Ecology: A Revival? J Ecosys Ecograph 8: 257.
Copyright: © 2018 Gaucherel C. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Select your language of interest to view the total content in your interested language
Share This Article
Recommended Journals
Open Access Journals
Article Usage
- Total views: 8362
- [From(publication date): 0-2018 - Dec 09, 2025]
- Breakdown by view type
- HTML page views: 7214
- PDF downloads: 1148