+44-3308187254
+44-3308187254
Antoine Al-Achi*
Campbell University, College of Pharmacy and Health Sciences, USA
Received date: November 15, 2016; Accepted date: November 16, 2016; Published date: November 21, 2016
Citation: Al-Achi A (2016) The Notion of Milliequivalence (mEq): A Brief Note. Clin Pharmacol Biopharm 5:e126. doi: 10.4172/2167-065X.1000e126
Copyright: © 2016 Al-Achi A. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Clinical Pharmacology & Biopharmaceutics
Pharmacists are often asked to prepare solutions containing electrolytes. Electrolytes solutions are used in medicine to replenish fluid and provide needed electrolytes to patients. The concentration of these electrolytes in solution is expressed in milliequivalence (mEq). One millieqivalent weight of any electrolyte is 1/1000 its equivalent weight. For example, sodium ion has an atomic weight of 23 g/mol and a valence of 1 equivalent/mol (Valence reflects the combining power of atoms. For example, two atoms of sodium combine with one carbonate group). Thus, one equivalent weight of sodium equals to its atomic weight, or there are 23 g of sodium per equivalent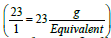
. The concentration unit, milliequivalence, was proposed specifically for ions because when ions combine together they always combine one equivalent weight to one equivalent weight. Thus, 23 g of sodium always combine with 30 g of carbonate ions (60 g/mol) (one equivalent weight of carbonate is 
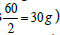. Moreover, one equivalent weight of any salt always contains one equivalent weight of the ion of interest. One equivalent weight of sodium carbonate (106 g/mol) 
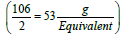contains one equivalent weight of sodium (23 g) and one equivalent weight of carbonate (30 g). The salt dibasic potassium phosphate (K2HPO4) is often used as a food additive because the US Food and Drug Administration (FDA) have this salt on its GRAS list (Generally Recognized as Safe). The equivalent weight of this salt depends on the ion of interest. With respect to potassium ions, the equivalent weight is 
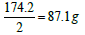(one millieqivalent weight is 0.0871 g or 87.1 mg). Stated otherwise, since one equivalent weight of potassium is 39 g and this salt contains (2 × 39 = 78 g), thus the weight of this salt that contains one equivalent weight of potassium is one-half its molecular weight, or 87.1 g. If this salt is used for its content of hydrogen ions, as the case for making a buffer solution, its equivalent weight (174.2 g/Equivalent) is the same as its molecular weight (174.2 g/mol). And, if this salt is used for its phosphate group 
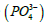its equivalent weight is
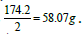Some applications may be focused on providing the 
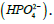In this case the equivalent weight is simply 
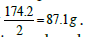It is important to mention here that for injectable preparations, phosphate salts are never expressed in milliequivalence units because a shift in the pH changes the type of salt from one form into another (from dibasic salt to monobasic salt, and vice versa) [K2HPO4 ↔ KH2PO4]. The concentration of phosphate salts in parenteral preparations is expressed in molar units (number of moles of the solute in one liter of solution). Occasionally, solutions may be labeled in normal units such as those for acids and bases. For example, chemists may prepare a 0.1 N solution of HCl. By definition, 1 N solution is the same as 1 Equivalent/L. Thus, the 0.1 N HCl solutions contain 0.1 Eq. of HCl/L, or 100 mEq/L.
For ions, milliequivalence is related to milliosmolar (the number of milliosmoles of a solute in one liter of solution; 1 osmole = 1000 mOsml) by the following expression:
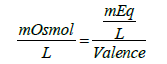(1)
An osmole is defined as the weight of a substance in grams that gives rise to one Avogadro’s number of particles (6.0221415 × 1023 particles/mol) in solution upon complete dissolution in water. Another definition of an osmole is derived from the colligative properties of solution. In this regard, an osmole is the weight of a substance in grams that upon complete dissolution in 1 kg of water produces an osmotic pressure elevation by 22.4 atm. at 0°C. In these calculations, one particle is considered to be an ion or a molecule. For example, NaCl when completely dissolved in water each molecule produces two ions, thus the number of “particles” produced upon complete dissolution is twice the original number of salt molecules, yet from the point view of the solution one NaCl molecule is a particle and each one of the ions produced is a particle. Furthermore, the nature of the solute is not important when calculating for colligative properties, because these properties depend primarily on the relative number of solute particles found in solution.) Based on this discussion, 1 molar solution of NaCl is equivalent to 2 osmolar (1 mole=2 osmoles of NaCl). In general: 1 molar solution of an electrolyte=(# of ions produced) × osmolar). For Na2CO3, 1 molar=3 osmolar because three ions are produced per molecule (Some textbooks use the term osmolal which is the number of osmoles of the solute in 1 kg of solvent. However, since most of the pharmaceutical solutions are considered diluted, the term osmolal may be considered to be equivalent to osmolar).
Take the case of a solution containing 1 mEq of potassium ions/L with a valence of 1 equivalent/mol yields 1 mOsmol of potassium ions/L. For calcium ions (40 g/mol), 1 mEq/L solution equals 0.5 mOsmol/L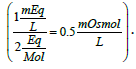 
A solution containing 40 mEq of Ca2+/L may be prepared by the addition of calcium chloride to purified water. The amount of calcium chloride monohydrate (CaCl2. H2O; 129 g/mol) needed to prepare one liter of solution would be 
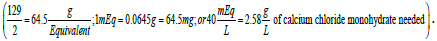In this situation, 2.58 g of the calcium salt are dissolved in enough purified water to prepare one liter of solution.
In the case of molecules, milliequivalence is related to milliosmolar by the following equation:
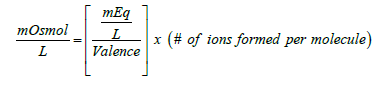(2)
Equation (2) is very similar to expression (1) except for the added term (# of ions formed per molecule). Thus, for the previous example of the calcium chloride monohydrate solution, the concentration of the calcium salt in solution expressed as mOsmol/L is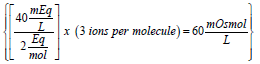 
(note that each molecule of CaCl2 upon complete dissociation in water produces 3 ions, one calcium and two chloride). Therefore, this solution may be labeled as 40 mEq/L or 20 mOsmol/L for its content of calcium (note that since the concentration of calcium chloride is 60 mOsmol/L and one-third of the salt is calcium, then one-third of 60 is 20 mOsmol of calcium ions/L). This solution contains 2.58 g of calcium chloride monohydrate/L or 60 mOsmol of the salt/L (or 20 mOsmol of calcium ions/L). Note that the solution may be also labeled as 40 mEq/L for its content of calcium chloride monohydrate (because one equivalent weight of the salt always contains one equivalent weight of the ion of interest).
In medicine, a 0.9% solution of NaCl is known as normal saline and is considered to be isotonic with blood (i.e., has the same osmotic pressure as that of blood). It is known that this saline solution freezes at (-0.52°C) (water freezes at 0°C (1 atm.), and the addition of sodium chloride to water to form normal saline reduces the freezing point to -0.52°C, according to the colligative properties of solution). (Freezing point depression, boiling point elevation, vapor pressure depression, and osmotic pressure elevation are all colligative properties of solution.) Pharmaceutical solutions of normal saline are often labeled as 308 mOsmol/L. This is evident from the fact that upon complete dissolution and dissociation in water, 0.9 g of NaCl per 100 mL solution converts to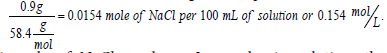 
and, since 1 mole of NaCl produces 2 osmoles in solution, the concentration 0.154 mol/L equals to
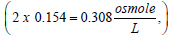or 308 mOsmol/L. It is interesting to note here that the same solution is 
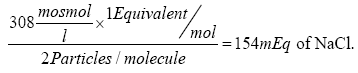of NaCl/L (according to Equation 2).
Isotonic solutions are prepared based on comparing the solution being prepared to the standard isotonic normal saline solution (0.9% NaCl). For instance, a drug solution that is hypotonic may be made isotonic by the addition of NaCl to its solution. Say, a drug solution (10 g of drug in 1 L solution; 1% solution) has an osmolarity of 200 mOsmol/L, then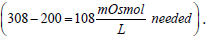 
Since 0.9% NaCl is 308 mOsmol/L then by proportion 
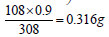of NaCl/100 mL or 3.16 g NaCl/L is needed to adjust for tonicity. Or stated otherwise, the drug solution contains an amount of drug osmotically equivalent to ((9 g – 3.16 g = 5.84 g) of NaCl). Thus, 10 g of the drug were equivalent in their osmolarity to 5.84 g NaCl, or 0.584 g of NaCl produced the same osmotic pressure increase as 1 g of the drug. This is known in pharmacy as the Sodium Chloride Equivalent value (E) for the drug (the weight of sodium chloride in grams that produces the same colligative property value as 1 g of drug). Pharmacists rely on four main methods in preparing isotonic solutions. All of these methods depend on the colligative properties of solution. These are freezing point lowering (cryoscopic), sodium chloride equivalent, White-Vincent, and Sprowls’ method. While the cryoscopic method uses the freezing point depression (a freezing point of -0.52°C is considered isotonic), the other three methods depend on the E value in their calculations.
A thorough knowledge of milliequivalence and its applications in medicine is essential to formulate solutions containing proper quantities of drugs and/or electrolytes, as well as to prepare isotonic solutions. For a more in-depth coverage of this topic, consult the references below or any other textbook of chemistry, biology, pharmacy, or nursing found at a health science library [1-6].
Make the best use of Scientific Research and information from our 700 + peer reviewed, Open Access Journals
