Treatment Effects and Risk Factors Evaluation in Longitudinal Studies: A Statistical Help for Data Analysis
Received: 15-Dec-2017 / Accepted Date: 12-Jan-2018 / Published Date: 19-Jan-2018
Abstract
This paper was inspired by the experience of the Authors research group composed by oncologist veterinarians and a biostatistician to evaluate treatments and prognostic factors with the aim to help veterinarians involved in longitudinal studies into evaluating and writing prognostic results.
Longitudinal studies are commonly analysed by techniques for survival data, taking into account for the time elapsed from the beginning of observation and the occurrence of an event related to treatment effect or disease course. The presence of incomplete follow-up information for some subjects requires specific descriptive and inferential statistical methods. Two literature datasets were analysed to show statistical models implementation techniques and to discuss statistical issues: I) A multicentre clinical trial on remission maintenance of children with acute Lymphoblastic leukaemia and II) A randomized clinical trial on advanced inoperable lung cancer. Data sets concerned studies on “humans”, nevertheless the peculiar data structure allowed to discuss some aspects which are common to survival analysis studies, regardless on subject’s characteristics. Log-rank test was used to compare survival curves for treatments and the relationship between Log-Rank test and univariate Cox model results was explained. As the evaluation of prognostic impact cannot be based only on p-values, the strength of the association between treatments and prognosis was estimated to take into account for the clinical relevance of results. On the second data set, beside of treatment, other clinical variables were available and a multivariate Cox model was applied. Model implementation was discussed concerning the coding of categorical variables and the relationship between continuous variables and model response. Suggested rules for the maximum number of covariates to be included in order to obtain reliable results were cited. Finally, the predictive ability of the model was discussed based on a measure of the area under ROC curve specific for survival data.
Keywords: Survival analysis; Prognosis; Interpretation of model results
Introduction
The present paper was born from the experience of cooperation among the Veterinarians and a Biostatistician (who are the Authors) in planning and analysing clinical studies. The cooperation started seven years ago and each study gave the opportunity to discuss both clinical and statistical issues. In this way the biostatistician became able to understand clinical research needs, in such a way to plan an adequate analysis, and veterinarians became able to interpret correctly statistical results, in such a way to evaluate results impact on their clinical practice. Several studies which concerned the evaluation of therapeutical strategies or the identification of potential risk factors, considering as end point the time elapsed from the beginning of the observation (e.g. date of the disease diagnosis, date of the surgery, starting date of pharmacological treatment) and the occurrence of an event which was related to the treatment failure or to the disease course were published and presented to meetings. Because much more debate arose around these studies than around other kinds of studies, the Authors decided to report some “critical aspects”. The Authors hope that reporting the critical aspects will be helpful to veterinarians, who have little experience on survival analysis, to evaluate and write results of prognostic studies. Since results of the statistical analysis should help clinicians in their “decision making process”, a correct methodology (by the Biostatistician) and a correct interpretation of model results (by the Veterinarian) is relevant.
To show the statistical issues two literature data sets which were standard in survival analysis books, were used:
• Dataset 1: A multicentre clinical trial on remission maintenance of children with acute Lymphoblastic leukaemia. The trial was published in [1] and data were reported at page 41 of the book [2].
• Dataset 2: A randomized clinical trial on advanced inoperable lung cancer (Veteran Administration Lung Cancer). Data were reported in the appendix A of the book [3].
Although data set concerned studies on “humans”, their peculiar characteristics allowed discussing some aspects which are common to survival analysis studies and, for readers who are confident with statistical packages, to give suggestions to perform the analysis by themselves.
Characteristics of Follow-Up Data, Common Statistical Approaches, Warnings and Some Proposed Improvements
The commonly considered study end-points are: the time to occurrence of a single event (e.g. death, independently by the cause), time to occurrence of a composite event (e.g. all kinds of disease relapses and death), time to occurrence of a specific event strictly related to the disease progression (e.g. death due to the disease). In order to perform a correct comparison among study results achieved on the same clinical condition it is important to detail which events were considered in the end points and how they were recorded.
When a small sample of individuals is evaluated, follow-up time and events for each individual can be shown and discussed, making statistical analysis not strictly necessary to understand results. Otherwise, data should be synthesized by descriptive statistics (e.g. mean, median, percentages) and inferential procedures should be considered to draw conclusions on the study results.
Follow-up data require descriptive and inferential statistical techniques which are specific for survival analysis. The techniques take into account peculiar characteristics of follow-up data: the study end-point may not be observed for all subjects. Some subjects may be free of the event at the end of the observation period and some subjects may be lost to follow-up. The probability of being free of the event during follow-up is commonly estimated by the Kaplan-Meier method. When a putative categorical prognostic factor (e.g. lymph node metastasis) is analysed, the most frequent applied procedure is to estimate the event free survival curve for each category (e.g. lymph node metastasis present vs. lymph node metastasis absent) and to compare those event free survival curves by Log-Rank test. To draw conclusions on the prognostic role of the putative prognostic factor only the p-value of the test is usually considered. However, to assess the “clinical relevance” of the prognostic factor “clinically useful” measures should also be provided. These measures could be related to the difference between end-point probabilities at a given time (risk differences), to the ratio between end-point probabilities at a given time (relative risks) or alternatively, to the differences between end-point rates (rate differences or hazard differences) or to the ratio between end-point rates (rate ratios or hazard ratios).
When several clinical and pathological variables are analysed, Cox model is used to evaluate their joint prognostic role (multivariate analysis). Cox model is based on a specific assumption which must be tenable for the correctness of the results (i.e.: for each variable hazard ratio should be constant over follow-up time and this is named “proportional hazard” [2]). The “optimal” approach is to include all the variables into the model to identify which variables have a “significant” prognostic role. Unfortunately, this approach is not always possible. Literature suggests rules on the maximum number of regressors to be considered in multivariate analysis so to obtain reliable results [4-6]. The maximum number of regressors depends on the number of observed events rather than on the number of individuals in the study. Care is also needed for the coding of quantitative and qualitative (categorical) variables in order to avoid possible biased prognostic information. For qualitative variables (e.g. Tumour Stage with categories I, II, III) a category is chosen as “reference” (e.g. Stage I) and the following two hazard ratios: Stage II/Stage I and Stage III/Stage I are obtained by the exponent of the Cox regression coefficients. If Stage II and Stage III are not distinct (considered in the same category), only one hazard ratio is estimated: Stage II or Stage III/Stage I and the clinical interpretation of model results differ from those above cited for the 3 Stage categories. To allow clinical usefulness of the model results, the categories should follow substantiated clinical criteria. For quantitative variables, a linear relationship between the logarithm of the hazard and the variable values is the simplest one. As an example, Age is a continuous variable and, under a linear relationship, the hazard ratio comparing the outcome of x years old subjects with the outcome of x+1 years old subjects is the same whatever is the subject age x. Therefore, the logarithm of the hazard ratio comparing the outcome of 2 years old subjects with the outcome of 1-year old subjects is the same of the logarithm of the hazard ratio comparing the outcome of 12 years old subjects with the outcome of 11 years old subjects. However, the linear relationship could be improbable (e.g. the logarithm of the hazard ratio comparing the outcome of 2 years old subjects with the outcome of 1-year old subjects could be less or greater than the logarithm of the hazard ratio comparing the outcome of 12 years old subjects with the outcome of 11 years old subjects). In such a case, a possible complexity of the shape for the relationship between continuous variables and model response should be investigated [7]. Statistical software outputs are tables containing regression coefficients, the standard errors and p-values. International guidelines suggest showing regression coefficients with the corresponding 95% confidence interval, because it is simpler to evaluate than standard errors [8-11].
A “statistically significant” result does not imply clinical usefulness. If the aim of the study is not only exploratory but it involves clinical decisions, useful insights are provided by a measure of the predictive performance of the model [12].
Data Presentation and Model Results
The results of the statistical analysis retrieved for the two selected data sets were used to discuss the following issues:
i) percentages of events, mean and median time are not always appropriate, ii) Log-Rank test: p-value is not a comprehensive evaluation and a related measure of prognostic association should be given, iii) interpretation of the statistical test: a p-value >0.05 does not mean that the variables do not have a prognostic role, iv) interpretation of Cox model results: hazard ratio, risk ratio, confidence intervals, v) coding of the variables in multivariate analysis and the maximum number of regressors allowed, vi) statistical significance and predictive ability.
Percentages of events, mean and median are not always appropriate
Dataset 1: A multicentre clinical trial on remission maintenance for children with acute Lymphoblastic leukaemia was designed to test whether patients who achieved complete remission using steroid could benefit from further treatment. Forty-two patients were randomized to receive maintenance therapy whit 6-mecaptourindine (6-MP; n=21) or placebo (n=21) [1,2].
Time to relapse (in weeks) of the two groups is reported as follows:
• Placebo 1,1,2,2,3,4,4,5,5,8,8,8,8,11,11,12,12,15,17,22,23 (all patients in placebo group had a relapse)
• 6-MP 6,6,6,6*,7,9*,10,10*,11*,13,16,17*,19*,20,22,23,25*,32*,32*, 34*,35* (some patients in 6-MP group were still in remission when the study was stopped and were considered as censored times, indicated by*).
The placebo group: Percentage of events: 100*(21/21) =100%
All patients had a relapse, but from this data presentation no information was retrievable on time when 100% was reached. Results should be referred as “the cumulative probability of relapse at 23 week was 1.0 or “the probability of remission after 23 weeks is 0”.
The probability of remaining free from relapse was 0.762 at 3 weeks, 0.571 at 6 weeks, and so on.
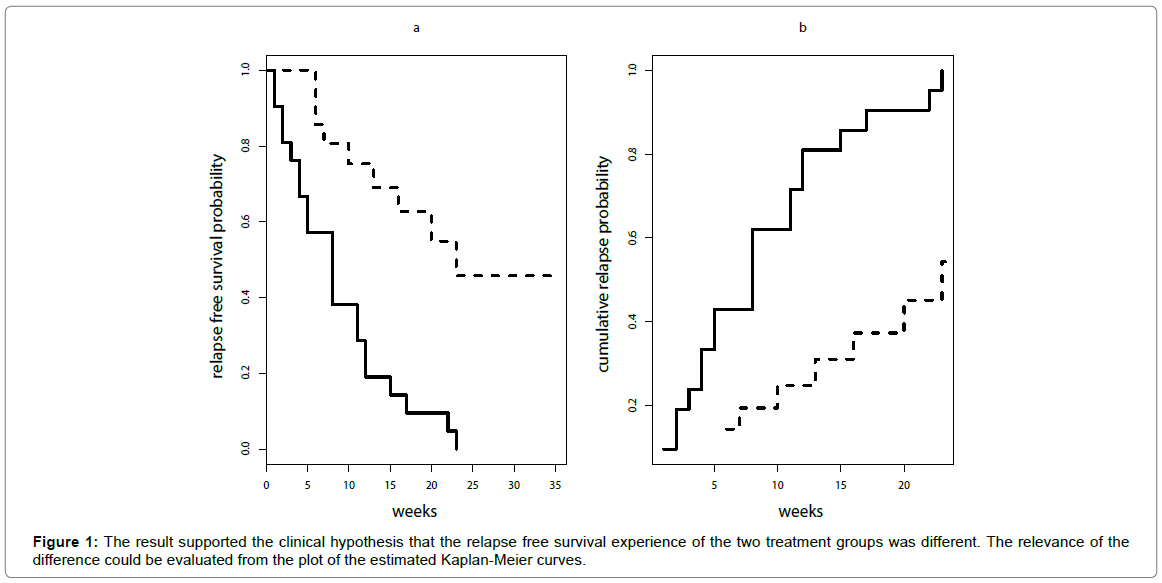
These are the estimates obtained by Kaplan-Meier method. The corresponding cumulative incidence curve can be easily obtained by 1-relapse free survival probability (Figure 1).
A relapse was observed for all patients in this group. Mean time to relapse and median time to relapse can be directly calculated from follow-up observation time: mean=8.67 weeks and median=8 weeks.
The 6-MP group
Nine patients with relapse were observed: 100*(9/21) =42.86% and the percentage of patients still in remission was 57.1%. The cumulative probability of relapse at 35 weeks was not 0.4286 but it was 0.608. The probability of remaining in remission after 35 weeks was not 0.571 but it was 0.392. It is matter of fact that the percentages previously calculated were wrong estimates. Why this difference? Twelve out of 21 patients at the end of the study were still in remission and for 11 patients the follow-up time was shorter than 35 weeks; we don’t know if they were still in remission at 35 weeks, we only know they were still in remission at 6,9,10,11,17,19,20,25,32,34 weeks, respectively.
The probability of relapse at a given time t can be calculated only on the group of patients who had not a relapse before t and whose status at t is known (i.e. at time t it is known if they had a relapse or if they were free from relapse). This group of patient is named “patients at risk” of relapse at time t. Patients whose status at time t is unknown (e.g. patients lost to follow-up before time t) cannot be considered in the group of patients “at risk” at time t. The cumulative probability of relapse at time t is obtained adding the probabilities of relapse for all times less or equal to t.
For example at 6 weeks all 21 patients were at risk, 3 patients had relapse and the probability of relapse was 3/21=0.143. At 7 weeks a more complex situation was observed, 3 patients relapsed at 6 weeks and 1 patient who was still in remission at 6 weeks was no longer observed after 6 weeks thus patients at risk were 21-4=17. At 7 weeks, 1 relapse was observed but the probability of relapse was not simply obtained by 1/17. In fact, a relapse at 7 weeks could be observed only if a patient was survived free from relapse till 7 weeks (1-3/21) thus the probability of relapse at 7 week was 1/17 x (1-3/21) and the cumulative probability of relapse at 7 week was 3/21+1/17 x (1-3/21) =0.193. The same procedure must be applied for all times and this was the criterion used for Kaplan-Meier estimation.
Median and mean time to relapse cannot be calculated directly from follow-up observation time, in fact time to relapse of patients who were still in remission at the end of the study was not known.
Median time to remission could be obtained from Kaplan-Meier estimation by searching the time corresponding to the relapse free probability of 0.5 (about 23 weeks).
The comparison between survival curves: the interpretation of the test and a measure of association between variables and prognosis
When survival curves for groups of patients characterized by different modalities of a covariate are estimated by Kaplan-Meier method, the most common statistical test used is Log-Rank. Two hypotheses are formulated on the population from which the case series is a sample: the null hypothesis of equal survival experience of the groups to be compared (Ho) and the alternative hypothesis between the survival experiences of the groups to be compared (Ha). In the simplest case of two groups the hypotheses are formulated as follows: Ho: λ1(t)=λ2(t) and Ha: λ1(t)=θ λ2(t), where λ(t) is a “key” quantity in survival analysis, known as “hazard of event” (the event rate at time t). The alternative hypothesis is that the hazard of event for the group 1 is θ times the hazard of event for the group 2 [2].
When p-value of the Log-Rank test is < 0.05 the commonly reported conclusion is “the difference between the two group is statistically significant” (i.e. the null hypothesis is rejected with the planned probability =0.05. It is accepted to reject the null hypothesis with a probability of a wrong conclusion = 0.05). Unfortunately, when p-value is > 0.05, the result is sometime wrongly interpreted as “the survival experience of the two groups in the population is equivalent”. A statistical test cannot “demonstrate” the trueness of a statistical hypothesis. If the null hypothesis is rejected the results on the sample are a “support” of the alternative hypothesis, giving a strong evidence that obtained results are “unlikely” to arise if the null hypothesis was true. If the null hypothesis is not rejected nothing can be stated on the evidence in favour of the null hypothesis. It is worth of note that p-value is not the most relevant criterion to evaluate differences between groups, it is also important that the observed differences are clinically relevant. A statistical test applied to a very large case series could provide a “statistically significant” result for a very small difference, which is not relevant from the clinical point of view [13]. On the other hand, a clinically relevant difference on a small case series could result as “not statistically significant “because of the low power of the test (i.e. the probability to correctly conclude that in the population the survival experience of the two groups are different). The observed difference could be “statistically significant” with a greater sample size, thus, in the situation of a clinically relevant difference with a p-value > 0.05 it is not correct to conclude on the equivalence of survival experience of the two groups in the population. A detailed discussion on the interpretation of statistical tests is reported on the Medical Statistical books ([14] among others) and in several tutorial papers ([15] among others).
For the leukaemia trial the result of the Log-Rank test was: Chi-square= 16.8 and p-value= 4.19 x 10-5 (<0.00001). This result supported the clinical hypothesis that the relapse free survival experience of the two treatment groups was different. The relevance of the difference could be evaluated from the plot of the estimated Kaplan-Meier curves (Figure 1a) but a summary measure of treatment clinical impact is not directly provided by Log-Rank test.
As the hypothesis underlying Log-Rank test is based on the ratio between hazards of events, a possible measure of clinical impact is the hazard ratio, which is assumed to be constant over follow-up. Proposed approaches to estimate hazard ratio based on Log-Rank, have been evaluated by Kitchin and Mock [16]. A simpler method was to use Cox model in which only treatment (coded 0 if 6-MP and 1 if placebo) was included as explanatory variable.
The exponent of Cox model regression coefficient is the estimated hazard ratio and for treatment in leukaemia data set it was 4.801. This means that the hazard of relapse of placebo treated patients was about 5 times the hazard of relapse of 6-MP treated patients. Relevant estimates should be reported in association with the hazard ratio: the corresponding 95% confidence interval (for treatment leukaemia data set was 2.14-10.77). Although the null hypothesis of hazard ratio equal to 1 was rejected, the 95% confidence interval was wide, thus providing the information of a low precision of the estimate.
If the cumulative probability of relapse within a follow-up time (t) is called “risk”, the relative risk was the ratio between the estimated cumulative probabilities of relapse of the two treatment groups at that time [17,18]. It could be easily shown from Figure 1b that the risk ratio was not constant over time and it was different from hazard ratio (4.81). For example, at 6 weeks the risk ratio was 2.30, at ten weeks was 2.50, and at twelve weeks was 2.00, thus, in this case, it cannot be reported that the risk ratio was 4.81.
Coding of the variables in multivariate analysis and the maximum number of regressors allowed
Dataset 2: One-hundred and thirty-seven patients with advanced inoperable lung cancer were randomly assigned to two chemotherapy treatments: standard or experimental. Other additional variables were collected for each patient: Karnofsky Performance Score (0=bad, 100=good), Time from Diagnosis to Randomization (months), Age (years), Prior Therapy (0=no, 1=yes), Cell Type (Squamous, Small, Adeno, and Large). Study primary end-point was the comparison of survival experience of the two treatment groups.
One-hundred and twenty-eight patients died (64 in both treatment groups) and nine were still alive at the end of follow-up period [3].
A first analysis could be performed only on the variable “treatment” because randomization should “guarantee” in probability the equal distribution of other variables in the two treatment groups.
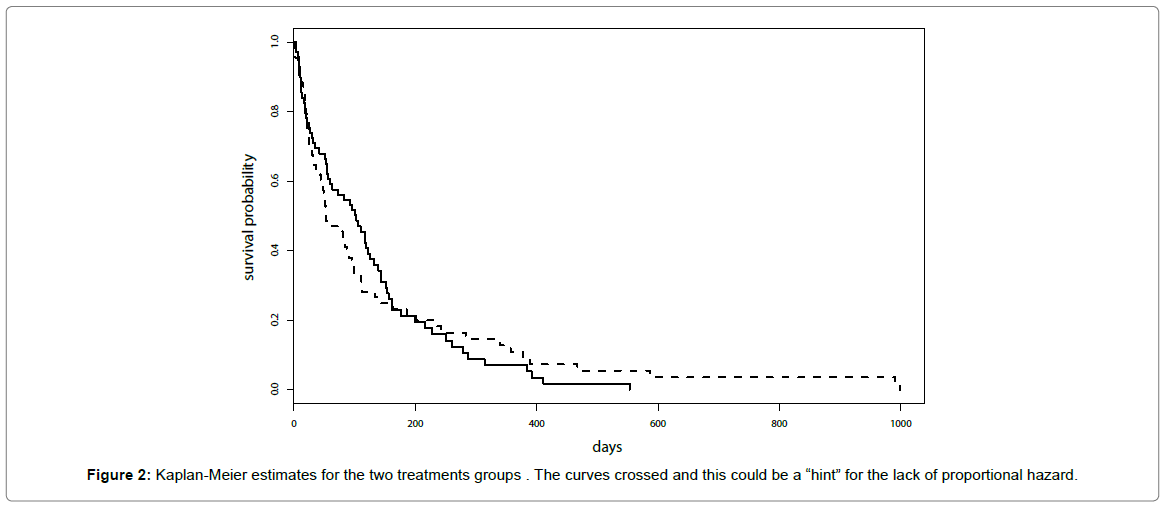
Kaplan-Meier estimates for the two treatments groups are reported in Figure 2 and similar results for the two treatments were suggested. It was worth noticing that curves crossed and this could be a “hint” for the lack of proportional hazard.
Results of the test for the proportional hazard did not provide support to the lack of proportional hazard (p-value=0.07 for Kaplan- Meier transform and p-value=0.14 for the identity transform).
Results of the Cox model including only the variable treatment (coded as 0 for control and 1 for experimental): Hazard ratio =1.018, 95% confidence interval: 0.7144 -1.45, p-value=0.922. Regardless p-value, the hazard ratio was very near to 1.0 thus a very similar result was obtained for the two treatments.
The adjustment of treatment effect including into the model other variables retained as “clinically relevant” by previously published paper and/or previous knowledge of disease course is still debated in clinical trials literature [19-21]. However, to illustrate multivariate analysis, the other 5 variables in the dataset were included in the regression model to “adjust” treatment effect. Some variables were quantitative (Karnofsky Performance Score, Time from Diagnosis to Randomization, Age) and others were qualitative (Prior Therapy, Cell Type).
How to include the variables in the model: Concerning the quantitative variables the simplest approach is assuming a linear relationship between the variable and model response (logarithm of the hazard) thus the variable can be included in the model without data transformation. This approach could be inadequate and the possible nonlinear relationship needs to be tested. It is not simple and model results are difficult to be represented. If categorisation of the variable can be performed, under clinical consideration, model results are simple to evaluate. Nevertheless it can be taken into account that categorisation may result in a loss of prognostic information.
Categorical variables must be included into the model by generating dummy variables. One of the categories is chosen as “reference” and each dummy variable allows estimating the ratio between the hazard of the category and the hazard of the reference one. For a variable with k categories k-1 dummy variables are needed. Thus, for Treatment and Prior Therapy, having two categories, one dummy variable was generated: Standard Treatment and No Prior Therapy were chosen as reference.
Cell Type was coded by 4 categories and three dummy variables were generated. Squamous was chosen as reference and the tree dummy variables allowed estimating the hazard ratio of Adeno vs. Squamous, Small vs. Squamous and Large vs. Squamous, respectively.
When Cox model is used for the multivariate analysis, it was recognized that a too-small ratio of events per variable (EPV) can affect the accuracy and precision of regression coefficients and their tests of statistical significance. It was suggested that 10 outcome events per predictor variable should be considered for the maximum number of regressors to be included into a multivariate regression model [4]. This rule was subsequently reconsidered suggesting a minimum of 5 outcome events per predictor variable [5]. It is worth of note that the number of regressors may not be equal to the number of variables, in fact for categorical variables the number of corresponding dummy variables need to be counted.
In dataset 2, 128 deaths were observed thus a maximum of 13 regressors (or a maximum of 26 regressors) should be included in multivariate Cox model. In the simplest model 8 regressors were considered: 5 for the categorical variables (1 dummy variable for Treatment, 1 dummy variable for Prior Therapy, 3 dummy variables for Cell Type) and 3 for the continuous variables (1 for Karnofsky Performance Score, 1 for Time from Diagnosis to Randomization, 1 for Age). In case of nonlinear relationship between the logarithm of hazard ratio and continuous variable, for the latter 3 variables a greater number of regressors may be considered to model a possible complex shape. A simple way to face nonlinear relationship is to model variables as polynomials (e.g. including as regressors Age, Age2, Age3). An improvement of this approach giving more flexibility is the use of cubic splines (the range of the independent variable is subdivided using K breakpoints. Within each breakpoint a third order polynomial is considered and polynomials are then joined at breakpoints, called “knots”, to obtain a smoothed fit). The putative presence of nonlinear relationship for the continuous variables was tested including into the model regression cubic splines [22,23]. No evidence of nonlinear effects was found (p-value= 0.3145, 0.9134, 0.816 for Karnofsky Performance Score, Time from Diagnosis to Randomization and Age, respectively). Results of the multivariate Cox model are reported in Table 1.
| Variable | Hazard Ratio | 95% C.I. | p-value* |
|---|---|---|---|
| Treatment | |||
| Experimental / Standard | 1.343 | 0.894-2.017 | 0.157 |
| Karnofsky performance score | |||
| 1 score increase | 0.968 | 0.957-0.978 | <0.0001 |
| Time from diagnosis to randomization | |||
| 1 month increase | 1.0001 | 0.982-1.018 | 0.993 |
| Age | |||
| 1 year increase | 0.991 | 0.973-1.010 | 0.349 |
| Prior therapy | |||
| Yes / No | 1.074 | 0.681-1.694 | 0.758 |
| Cell Type | |||
| Adeno / Squamous | 3.307 | 1.834-5.965 | <0.0001 |
| Small / Squamous | 2.367 | 1.380-4.060 | 0.002 |
| Large / Squamous | 1.494 | 0.858-2.600 | 0.156 |
Legend: For categorical variables the notation C/R means that HR is the ratio between the hazard of death for the category C and the hazard of death for the category R (the reference category). e.g 3.307 is the ratio between the hazard of death for the category Adeno and the hazard of death for the category Squamous (reference category).
For continuous variables the notation “1 unit increase” means that HR is the ratio between the hazard of death for the value of the variable j+1 and the hazard of death for the value of the variale j, which is constant for all values of the variable.
e.g. 0.991 is the ratio between the hazard of death for age 31 and the hazard of death for age 30 which is equal to the ratio between the hazard of death for age 51 and the hazard of death for age 50 and which is equal to the hazard ratio of all comparisons between age j+1 and age j;
95% C.I. : 95% confidence intervals;
*p -value of the Wald test.
Wald test was used to test the null hypotesis : Cox regression coefficient = 0 versus the alternative hypothesis: Cox regression coefficient ≠ 0.
Table 1: Results of the multivariate Cox model for dataset 2: Estimated Hazard ratios of death and 95% confidence intervals.
With respect to the univariate analysis, the hazard ratio for the category “Treatment” was increased (from 1.018 to 1.343). The hazard ratio for Prior Therapy is near to 1, suggesting a small prognostic effect of the variable, regardless of statistical significance. A greater impact was observed for Cell Type where the hazard of death for patients with Adeno and Small cancer is more than double than the hazard of death for patients with Squamous cancer.
For continuous variables it is reported the hazard ratio for a “unit increase”: if the hazard ratio is less than 1.0, greater is the value of the variable more favourable is the prognosis, and vice-versa. Nevertheless it is common that estimated hazard ratios are near to 1.0 also for well-known prognostic factors. Differently to the categorical variables, these results cannot be interpreted necessarily as a “small” prognostic impact.
As an example, for Karnofsky Performance Score, the hazard ratio for a Score s+1 with respect to the Score s was 0.968. For a variable whose values ranged from 1 to 100 it was not expected that one unit increase of the Score could result in a “strength” prognostic impact.
In this case it could be preferable to show results for a “clinically meaningful” increase (e.g. 10 units increase: hazard ratio =0.720).
The predictive ability
The predictive ability of a Cox model result can be evaluated by the area under ROC curve for censored survival data, named “Harrell’s C index”. This index ranges between 0.5 (lack of predictive ability) and 1 (perfect predictive ability) [12,22]. The estimated predictive ability was 0.74 for the Cox model results reported in Table 1. The model included both variable whose impact was “statistically significant” and variable whose impact was not “statistically significant”. Considering a model including only statistically significant variables (Karnofsky Performance Score and Cell Type), the model predictive ability was 0.73, suggesting a negligible improve provided by the non-significant variables.
When Karnofsky Performance Score was excluded the predictive ability was 0.61 and when Cell Type was excluded the predictive ability was 0.71, suggesting a contribution of Karnofsky Performance Score greater than the contribution of Cell Type. When both the above mentioned variables were excluded the predictive ability was negligible (0.52).
Conclusion
The above considerations concern only the “most frequent discussed items”. We hope this paper could stimulate clinicians to read accurately statistical analysis results and avoiding to decide only on the basis of p-values. The cooperation between clinicians and biostatisticians could help clinicians to be more confident with statistical methods and could provide insights to evaluate the relevance of results taking into account also an adequate statistical analysis.
The attitude of some clinicians is to privilege papers where data are presented with currently adopted statistical methods because they believe this is always the best approach. This is not necessarily true. In fact some studies could require alternative statistical modelling to have a deeper insight to the prognostic impact of therapeutical strategies. Unfortunately, statistical methods which are not currently adopted are sometimes considered with concerns irrespectively to the clinical relevance of results. The collaboration among clinicians and biostatistician can help to remove uncertainty in order to evaluate new approaches and to improve the planning and the analysis of clinical studies.
Several other statistical issues on survival analysis could be faced; two examples are cited in the follow.
In the considered examples only additive models are applied, avoiding to assume the possible presence of prognostic synergism between variables. In this case multivariate model must include specific “interaction” terms and results are more complex to show and to interpret. For this reason, interaction effects should be considered only under specific clinical hypothesis on their meaning.
A further complication is when the focus is on the prognosis related to a specific unfavourable event in presence of the occurrence other events which avoid the observation of the event of interest. This condition is known as “competing risks”. A typical example of competing risks is death for the disease in presence of individuals whose cause of death can be related to the disease or not related to disease. The occurrence of a death not related to the disease avoids the observation of death related to the disease for that patient thus the two causes of death compete to be observed. In the presence of competing risks, Kaplan-Meier survival curves and Cox model are not appropriate to estimate the event probability during follow-up and to evaluate the prognostic effect of the covariates. Crude cumulative incidence curves and sub-distribution regression models are suitable for the analysis of competing risks data [24-26].
Analysis of competing risks was not considered in this paper as it is peculiar and it requires a separate processing.
Acknowledgement
The Authors thank Patrizia Lamusta who help editing manuscript.
References
- Freireich EJ, Gehan E, Frei E, Schroeder LR, Wolman IJ, et al. (1963) The effect of 6-mercaptopurine on the duration of steroid-induced remissions in acute leukemia: A model for evaluation of other potentially useful therapy. Blood 21: 699-716.
- Marubini E, Valsecchi MG (2004) Analysing survival data from clinical trials and observational studies. John Wiley & Sons, Chichester. 15.
- Kalbfleisch JD, Ross LP (2002) "Relative risk (Cox) regression models. The Statistical Analysis of Failure Time Data, Second Edition. 95-147.
- Peduzzi P, Concato J, Feinstein AR, Holford TR (1995) Importance of events per independent variable in proportional hazards regression analysis II. Accuracy and precision of regression estimates. J Clinical Epidemiology 48: 1503-1510.
- Vittinghoff E, McCulloch CE (2007) Relaxing the rule of ten events per variable in logistic and Cox regression. Am J Epidemiology 165:710-718.
- Lydersen S (2015) Statistical review: frequently given comments. Annals of the Rheumatic Diseases 74: 323-325.
- Leffondré K, Jager KJ, Boucquemont J, Stel VS, Heinze G (2013) Representation of exposures in regression analysis and interpretation of regression coefficients: basic concepts and pitfalls. Nephrology Dialysis Transplantation 29: 1806-1814.
- Von EE, Altman DG, Egger M, Pocock SJ, Gøtzsche PC, et al. (2014). The Strengthening the Reporting of Observational Studies in Epidemiology (STROBE) Statement: guidelines for reporting observational studies. Intern J Sur 12: 1495-1499.
- Schulz KF, Altman DG, Moher D (2010) CONSORT 2010 statement: updated guidelines for reporting parallel group randomised trials. BMC Medicine 8: 18.
- Grindlay D (2015). Reporting guidelines: how can they be implemented by veterinary journals? Equine Veterinary J 47: 133-134.
- Christley R (2015) Statistical guidelines for Equine Veterinary Journal. Equine Veterinary J 47: 131-132.
- Seth LT, Aban I (2017) Quantifying predictive accuracy in survival models. J Nucl Cardiol. 24: 1998-2003.
- Van Rijn MH, Bech A, Bouyer J, Van Den Brand JA (2017) Statistical significance versus clinical relevance. Nephrology Dialysis Transplantation. 32 (suppl_2): ii6-ii12.
- Armitage P, Geoffrey B, Matthews JNS (2002) Statistical methods in medical research. John Wiley & Sons.
- Lam SW, Bauer SR, Yang W, Miano TA (2017) Statistics Myth Busters: Dispelling Common Misperceptions Held by Readers of the Biomedical Literature. Ann Pharmac 51: 429-438.
- Kitchin GRM, Mock PA (1991) A comparison of two simple hazard ratio estimators based on the logrank test. Statistics in Medicine 10: 749-755.
- Symons MJ, Moore DT (2002) Hazard rate ratio and prospective epidemiological studies. J Clinical Epidem 55: 893-899.
- Stare J, Maucort BD (2016) Odds Ratio, Hazard Ratio and Relative Risk. Metodoloski Zvezki. 13: 59-67.
- Pocock SJ, Assmann SE, Enos LE, Kasten LE (2002) Subgroup analysis, covariate adjustment and baseline comparisons in clinical trial reporting: current practice and problems. Statistics in Med 21: 2917-30.
- Tsiatis AA, Davidian M, Zhang MLX (2008) Covariate adjustment for twoâ€sample treatment comparisons in randomized clinical trials: A principled yet flexible approach. Statistics in Med 27: 4658-4677.
- Kahan BC, Jairath V, Doré CJ, Morris TP (2014) The risks and rewards of covariate adjustment in randomized trials: an assessment of 12 outcomes from 8 studies. Trials 15: 139.
- Harrell FE, Lee KL, Mark DB (1996) Multivariable prognostic models: issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors. Statistics in Med 15: 361-87.
- Shepherd BE, Rebeiro PF, Caribbean Central, South America network for HIV epidemiology (2017) Brief Report: Assessing and Interpreting the Association between Continuous Covariates and Outcomes in Observational Studies of HIV Using Splines. JAIDS J Acquired Immune Deficiency Syndromes. 74: e60-e63.
- Beuscart JB, Pagniez D, Boulanger E, de Sainte FCL, Salleron J, et al. (2012). Overestimation of the probability of death on peritoneal dialysis by the Kaplan-Meier method: advantages of a competing risks approach. BMC Nephrology 13: 31.
- Boracchi P, Orenti A (2015) Survival Functions in the Presence of Several Events and Competing Risks: Estimation and Interpretation Beyond Kaplan-Meier. International J Statistics in Medical Res 4: 121-139.
- Austin PC, Lee DS, Fine JP (2016) Introduction to the analysis of survival data in the presence of competing risks. Circulation 133: 601-09.
Citation: Boracchi P, Ferrari R, Groppetti D, Stefanello D (2018) Treatment Effects and Risk Factors Evaluation in Longitudinal Studies: A Statistical Help for Data Analysis. J Vet Med Health 2:103.
Copyright: © 2018 Boracchi P, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Select your language of interest to view the total content in your interested language
Share This Article
Recommended Journals
Open Access Journals
Article Usage
- Total views: 5067
- [From(publication date): 0-2018 - Dec 08, 2025]
- Breakdown by view type
- HTML page views: 4047
- PDF downloads: 1020