Research Article Open Access
Period is Going to be Faster When the Earth-Moon Distance Increased According to IERS Actual Data
| Sami Esmail | |
| Corresponding Author : | Sami Esmail |
| Received September 27, 2010; Accepted December 18, 2010; Published December 20, 2010 | |
| Citation: Esmail S (2010) Period is Going to be Faster When the Earth-Moon Distance Increased According to IERS Actual Data. J Earth Sci Climat Change 1:103. doi:10.4172/2157-7617.1000103 | |
| Copyright: © 2010 Esmail S. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. | |
Visit for more related articles at Journal of Earth Science & Climatic Change
Abstract
If a small body of mass (m) orbits a large body of mass (M) then, the sidereal rotation period of the large body (M) may be calculated by the rotational equation.The earth rotation period is going to be faster when the earth-moon distance increased according to IERS actual data. Earthquakes of the upper range are distinctly related to rotational parameters of the Earth lunar declination.The earthquakes increased when the lunar declination is moving toward the earth equator (when the earth rotation are going to be faster).A perfect correlation between lunar declination and the changes of leap seconds.(UT1-UTC)-(UT1- UTC).A very good correlation between earthquakes and the changes of leap seconds.(UT1-UTC)-(UT1-UTC).The Earth rotation acceleration of 29 degree declination is more that of 18.6 declination, this lead to more earthquakes in 29 degree lunar declination.
| Introduction |
| The moons are “driving” the rotation of their parent planet in the same way, as sun’s rotation is being controlled by the planets. Paul D. Jose calculated and analyzed sun’s motion around the center of mass of the solar system for the period from 1843 to 2013 [8]. He compared his research results with the then available sunspot curves. He concluded that “Certain forces exerted upon the Sun by the planets are the cause of the sunspot cycle”. There is considerable uncertainty about the even most basic properties of mass, radii and density of Pluto and Charon The earthquakes may be effected by the Earth rotation, and lunar declination. Weems and perry Jr.(1989) found strong correlation between major earthquakes and lunar declination The degree of Lunar Declination varies yearly though an 18.5 year “Saros Cycle” which governs how the Moon’s orbit intersects the Earth’s. The Declination is the measure of how “tilted” the Moon’s Orbit has become, which ranges from 18.7 to 29 degrees. Extreme lunar declination years tend to have extreme storms and seismic activity. Think Hurricane Katrina, the December 2004 Sumatran earthquake and monster tsunami: these natural disasters accompanied the most recent peak in the lunar declination cycle. |
| Determination of Sidereal rotational period |
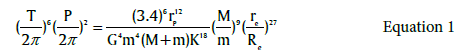 |
| Where: |
| T=Sidereal rotation period of the large body (sec) |
| P=The orbital period of the mass center of all satellites that orbit large body (sec) |
| K=Moment of inertia factor of the large body. |
| M=Large body mass (kg) |
| m=Total mass of all satellites that orbit the large body (kg) |
| a=Semi major axis of the mass center of all satellites that orbit large body (meter) (in table 3) |
| re =Equatorial radius of all satellites that orbit large body (meter) |
| rp =Polar radius of all satellites that orbit large body (meter) |
| Re= Radius for the large body which in the same orbital plane of all satellites that orbit large body (meter) |
| Re was calculated as the equatorial radius of the large body (meter) as the changes has a little effect. |
| G=gravitational constant = 6.67300 × 10-11 m3 kg-1 s-2. |
| The equation results |
| The rotation period (T) results from equation (1) |
| Determination of Earth rotation period |
| M=5.9736E+24 (kg) |
| Re= 6.3781E+6 (meter) |
| The Earth has one satellite (the Moon) |
| P=27.3 days |
| m=7.35E+22 (kg) |
| re =1738100 (meter) |
| rp =1736000 (meter) |
| From equation 1, (T) of Earth is 23.96 |
| Determination of Mars rotation period |
| M=6.4185E+23 (kg) |
| Re= 3397000 (meter) |
| There are two satellites orbit Mars |
| m= Total mass of all satellites that orbit the large body Mars (kg) |
| = m1 (Phobos)+m2 (Deimos) =1.3E+16 |
| a=Semi major axis of the center of mass of all satellites that orbit Mars (meter), so we can calculate (P) |
| =(m1 a1 +m2 a2 )/(m1 +m2 )=1.1977E+7 (meter), so we can calculate (P) for this mass |
| re= Equatorial radius of the total satellites (meter) |
| re=[(r1)^3+(r2)^3]^(1/3)=[(13400)^3+(7500)^3)]^(1/3)=14128 (meter) |
| rp= Polar radius of the total satellites (meter) |
| rp=[(r1)^3+(r2)^3]^(1/3)=[(9200)^3+(5200)^3)]^(1/3)=9714 (meter) |
| From equation 1, (T) of Mars is 24.36 |
| Determination of Jupiter, Saturn, Uranus, Neptune, Pluto, Haumea and sun rotation periods |
| By the same way, we can calculate the rotation period (T) from equation 1 as shown in Table (3) |
| All moons of small masses are negligible according to the equation results. |
| The earth rotation period is going to be faster when the earthmoon distance increased according to IERS actual data. (UT1-UTC)- (UT1-UTC) |
| The value (UT1-UTC)-(UT1-UTC) is to indicate the earth rotation period difference for any two successive days If (UT1-UTC) for today is less than that (UT1-UTC) of yesterday, then the earth rotation period time of today is less than that of yesterday. In other words, the earth speed is going to be faster for today than yesterday. |
| From Figure(3) and (4)(included as supplementary data), it is very clear that, when the earth-moon distance increased, the earth rotation period is going to be faster according to IERS data in (Figure 3 (included as supplementary data)). |
| From Figure (3) and Figure(4) (included as supplementary data), when the earth-moon distance decreased, the earth rotation period is going to be slower. |
| From Figure(3) and Figure(5) (included as supplementary data), when the earth rotation period (T) decreased from equation (1), the earth rotation period is going to be faster according to IERS data in (Figure 3 (included as supplementary data)). |
| The relationship between Earth rotation rate (UT1-UTC)-(UT1- UTC) and Earthquakes (more than or equal to 5.4) |
| From Figure (6 (included as supplementary data)), 85% of the earthquakes appears after the peak points when the earth rotation rate (UT1-UTC)-(UT1-UTC) decreased (The earth rotation acceleration is positive) |
| From Figure (7 (included as supplementary data)), 60% of the earthquakes appears after the peak points when the earth rotation rate (UT1-UTC)-(UT1-UTC) decreased (The earth rotation acceleration is positive) |
| From Figure (8 (included as supplementary data)), 82% of the earthquakes appears after the peak points when the earth rotation rate (UT1-UTC)-(UT1-UTC) decreased (The earth rotation acceleration is positive) |
| The relationship between Earth rotation rate, lunar declination and Earthquakes |
| The period is from 10/Jul/2006 to 23/Nov./2006 (lunar declination is 29 degree) |
| The Lower points in Figure (9 (included as supplementary data)) represent the highest speed of the earth rotation. (close to the earth equator) |
| The Lower points in Figure (10 (included as supplementary data)) represent the Min. Lunar declination. |
| The Peak points in Figure (11 (included as supplementary data)) represents the Max.earth radius in the lunar orbital plane. (the equator radius) |
| The Earth rotation rate reaches to its Max. When lunar declination is zero. (The highest Earth diameter) |
| There is a perfect correlation in the three curves. |
| From Figure (9), Figure (10) and Figure (11) (included as supplementary data), the Earth speed increased when the lunar declination decreased. |
| The Earth rotation acceleration of 29 degree declination is more that of 18 declination, this lead to more earthquakes in 29 degree lunar declination. |
| The period is from 9/Oct/1997 to 22/Feb./1998 (moon declination is 18 degree) |
| The Lower points in Figure (12 (included as supplementary data)) represents the highest speed of the earth rotation.(close to the earth equator) |
| The Lower points in Figure (13 (included as supplementary data)) represent the Min. Lunar declination. |
| The Peak points in Figure (14 (included as supplementary data)) represent the Max earth radius in the lunar orbital plane. |
| The Earth rotation rate reaches to it’s Max. when lunar declination is zero. (the highest Earth diameter) |
| There is a perfect correlation in the three curves. |
| From Figure (12), Figure (13) and Figure (14) (included as supplementary data), the Earth rotation speed increased when the lunar declination decreased. |
| The Earth rotation acceleration of 18.7 declination is less that of 29 declination, this is the main reason of decreasing earthquakes in 18.7 degree lunar declination. |
| Conclusion |
| If a small body of mass (m) orbits a large body of mass (M) then, may be we can calculate the sidereal rotation period of the large body (M). The Earth rotation period is going to be faster as a result of increasing Earth- Moon distance. From the rotation equation, the Earth is fastening it’s rotation period by -0.43 milliseconds/century. The Moment of inertia factor of Haumea may be expected to be 0.37 from equation (1).The Earth rotation acceleration of 29 degree declination is more that of 18 declination, this lead to more earthquakes in 29 degree lunar declination. The positive earth rotation acceleration is the main reason of the seismic activity. |
| Acknowledgements |
| Thanks to Eng. Franz J. Heeke; (Germany) for his useful internet web. |
| Thanks to Dr. Jerald Lee ; (USA) for his useful internet discussion and advice. |
References
|
Relevant Topics
- Atmosphere
- Atmospheric Chemistry
- Atmospheric inversions
- Biosphere
- Chemical Oceanography
- Climate Modeling
- Crystallography
- Disaster Science
- Earth Science
- Ecology
- Environmental Degradation
- Gemology
- Geochemistry
- Geochronology
- Geomicrobiology
- Geomorphology
- Geosciences
- Geostatistics
- Glaciology
- Microplastic Pollution
- Mineralogy
- Soil Erosion and Land Degradation
Recommended Journals
Article Tools
Article Usage
- Total views: 13637
- [From(publication date):
December-2010 - Dec 23, 2025] - Breakdown by view type
- HTML page views : 8985
- PDF downloads : 4652
