Analytical Vth, DIBL and Swing with and without Effective Conducting Path Effect (ECPE) for the Submicronic SDG FD SOI MOSFET

The electronic industrial world is in continuous search for an amelioration of the speed and the consumed power of the MOSFET device. But, with the miniaturization of the shape, governed by the ITRS roadmap [1], this component has shown its defects due to the parasitic effects. Among these undesirable effects, the so called short channel effects (SCEs), which minimize the MOSFET performances [2] and perturb the IC function.

The microelectronic industrials have sought to avoid these defects. The MOSFET structure on silicon with multiple gates [3-6] has proved successful in increasing the duration of the miniaturization and improving the compound performances taking into consideration the preservation of the planar silicon technology.

Despite its complex technological realization, the Symmetric DG FD SOI MOSFET remains one of the most interesting and encouraging compound to realize the Ultra-Deep Sub-Micronic (UDSM) structure and throughout augment density of integration.

Many models [7-13] have been developed to examine the performance of components. In this paper, we will put the evanescent model and the polynomial model with and without the ECPE into consideration to find out their convergence points for the study of the SDG FD SOI MOSFET. We solve the 2D poisson equation and we, analytically, analyze the SCEs via the dispersion study of the surface potential and the threshold voltage along the channel as well as the DIBL effect and the sub-threshold swing. The natural scale length for the polynomial model λ_p and its corrected form λ_pc including the ECPE are mentioned. The analysis of the SCEs allows us to locate the convergence points of the utilized models. We confirm these convergence situations by simulator data and/or some measures.

Surface potential and threshold voltage

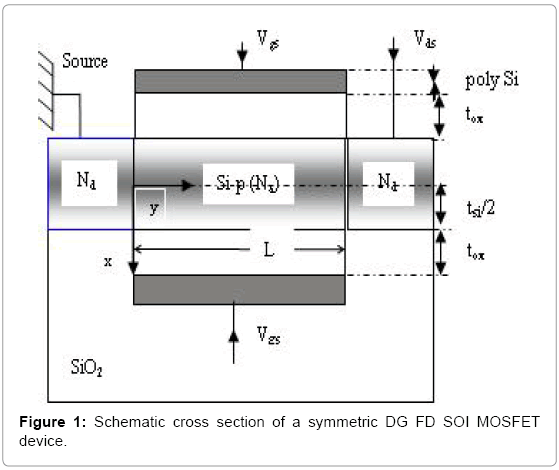
Figure 1 illustrates the cross section of the symmetrical DG SOI MOSFET device under fully depleted conditions and the inversion charge is neglected in regard to that of the of the depletion. We define by L, distance between source and drain, the channel length. t_ox and t_si represent respectively the thickness of the frontal oxide and the silicon body thickness. N_a is the silicon doping in the channel and N_d is the doping concentration of the source and drain regions. ε_si and ε_ox represent respectively the dielectric permittivity of the silicon film and the silicon dioxide.

Figure 1: Schematic cross section of a symmetric DG FD SOI MOSFET device.

The evanescent model supposes that the electrostatic potential in the silicon film, overlapped between both grids, is represented, according to the superposition principle, by φ(x,y) = φ₁(x)+ φ₂(x,y). φ ₁(x) is the solution of Poisson equation for a long channel and φ₂(x,y) is the solution of the Laplace equation and contain the short channel effect [14].

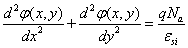(1)

The necessary boundary conditions of φ₁ and φ₂ to define φ(x) are as follow:

For φ₁:

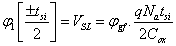
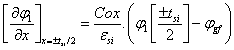
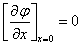
Where φ_gf = V_gf-V_fb, V_SL represents the surface potential for a long channel at 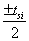; V_fb is the flat band voltage at the interface grid oxide – poly-silicon substrate.

C_ox =[ε_ox/t_ox ] is the frontal oxide capacitance and Csi = [ε_si/t_si ] is the silicon body capacitance.

For φ₂:

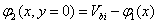
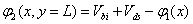
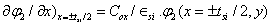
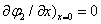
Where 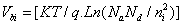denotes the built-in voltage between the source/drain end.

The frontal surface potential is defined as:

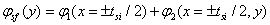
and written as follow:

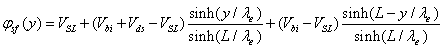(2)

Where λ_e represents the characteristic length for the evanescent model and verify the follow equality:

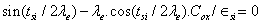(3)

The threshold voltage is defined as a grid voltage (V_gf=V_th) for φ_sf=2∅_B at y=y₀ where 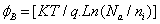is the Fermi potential in the channel and y₀ is the minimum surface potential abscise. This leads to write V_th as the form:

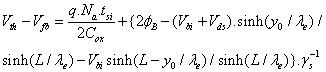(4)

Where γ_s denotes the short channel effects [15] and written as:

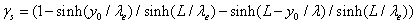
The gradient of threshold voltage is defined as ΔV_th =V_th0-V_th where V_th0 denotes the threshold voltage for a long channel SDG FD SOI MOSFET and written as:

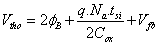(5)

DIBL parameter

For the SDG FD SOI MOSFET with short channel, the surface potential minimum increase with the drain bias. Thus, the short channel effect is attributed to the penetration of the electric field line, of the drain-channel junction, in the channel resulting in the potential barrier lowering (DIBL effect). This leads to the decreasing of the threshold voltage.

The ℜ parameter defined by 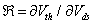evaluates the DIBL effect and written as:

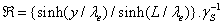(6)

Sub-threshold swing

The sub-threshold slope, appealed swing, is defined as the grid voltage that modifies the drain current under a threshold of a decade and written as

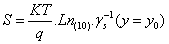(7)

Where y₀ is the minimum surface potential abscise.

Without the ECPE

Taking into account the polynomial model which considers the conduction current is at the surface of the silicon body and supposes parabolically the electrostatic potential profile in the vertical direction [6,10].

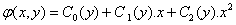(8)

Using the classical boundary conditions:

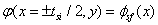
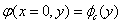
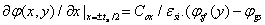
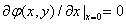
and writing the Poisson equation as 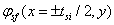, we deduce the polynomial characteristic length

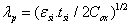(9)

Including the ECPE

The notion of the ECPE supposes that the gravity centre of the conduction current is at x=d_eff. The presentation of the electrostatic potential φ( x, y) at x=d_eff allows us to bring about a correction to polynomial characteristic length λ_p.

The new corrected characteristic length corresponding to the polynomial model including ECPE is:

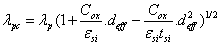(10)

The key factor d_eff, which illustrates the variation of scaling nature length λ_pc with substrate doping density, is so-called depth of the effective conducting path and it presents the location where the punch through current mainly occurs at subthreshold conduction with ECPE conducting mode [10].

The evanescent model and the polynomial model with and without the ECPE are utilized to analysis the short channel effect with the intention of searching the situations of their convergence.

To verify the analytical models of the convergence of SCE’s, the graphs illustrating le surface potential, the threshold voltage, DIBL and swing were plotted, compared and verified by measurement data. The same work for the conventional MOSFET prove that the convergence situation for the evanescent model and the polynomial model including ECPE is at d_eff=0.5t_si [16] and at d_eff=0.35t_si [17] for the single-gate SOI MOSFET device.

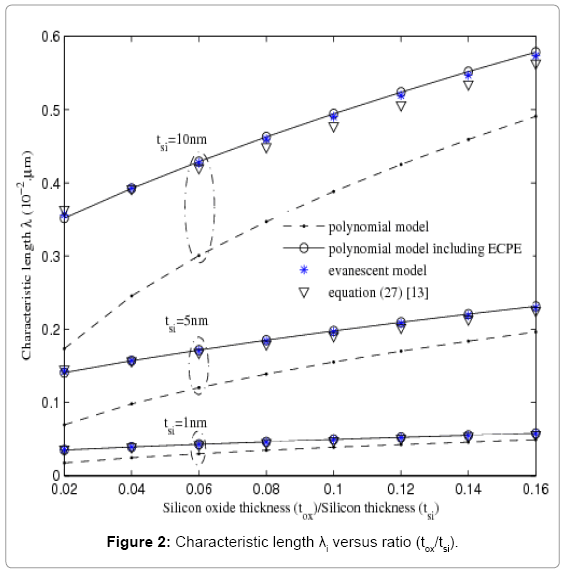
For the three models, figure 2 shows the evolution of the characteristic length λi (i=e, p or/and pc) as a function of ratio (t_ox/ t_si) for N_a=4.10¹⁷cm^-3, V_ds=0.5V and for a large range of t_si (t_si=1,5 and 10nm). We notice an adequate convergence, at d_eff=0.25t_si, between the evanescent model and the polynomial model including the ECPE. We also see that this convergence situation coincide with the data of equation 27 cited by Chen [13].

Figure 2: Characteristic length λ_i =5 versus ratio (t_ox/t_si).

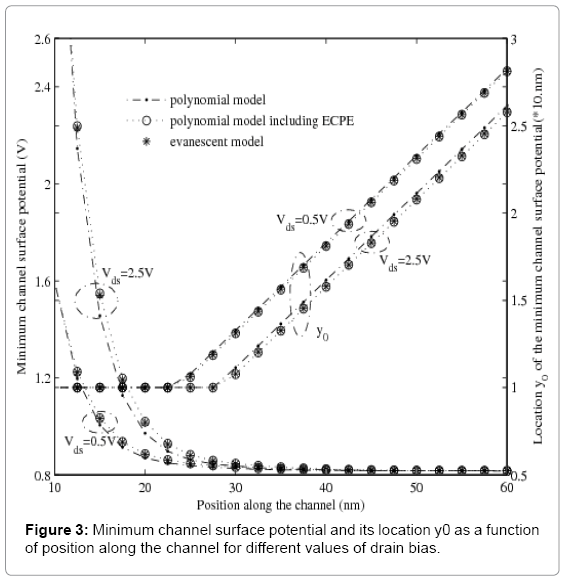
Figure 3 presents the evolution of the surface potential minimum and its position along the channel for the submicronic SDG FD SOI MOSFET device and for V_ds=0.5 and 2.5V. The results, and on a large scale of drain bias, show a good agreement between the evanescent model and the polynomial model including the ECPE at d_eff=0.25t_si.

Figure 3: Minimum channel surface potential and its location y0 as a function of position along the channel for different values of drain bias.

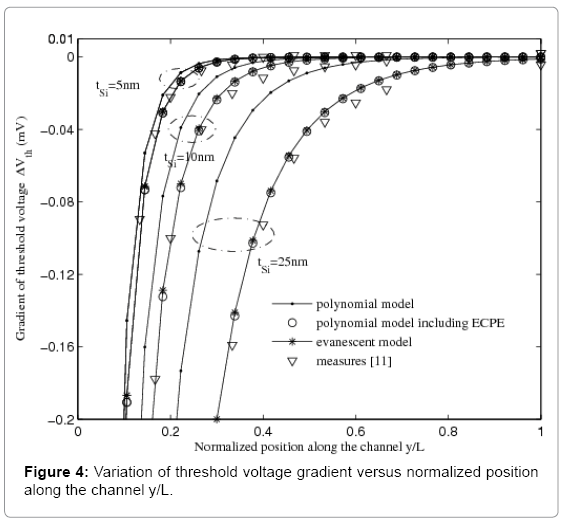
Figure 4 illustrates the evolution of the threshold voltage gradient in regard to the normalized position to L along the channel for L=150nm, V_ds=1.5V, t_ox=1.5nm and for t_si=5, 10 and 25nm. These results prove a perfect agreement, at d_eff=0.25t_si, between the evanescent model and the polynomial model including the ECPE with Jaju’s measurements [11].

Figure 4: Variation of threshold voltage gradient versus normalized position along the channel y/L.

As the drain voltage increases, the channel barrier and the threshold voltage are reduced. This is called Drain Induced.

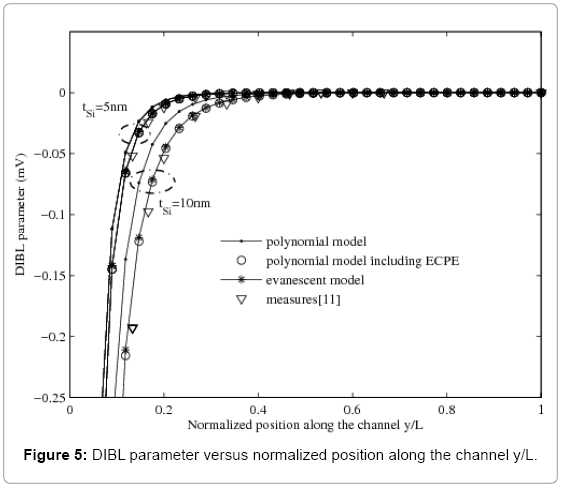
Barrier lowering. Figure 5 shows the evolution of the DIBL parameter as function of normalized position along the channel for the ultra-thin SDG FD SOI MOSFET with L=150nm, V_ds=1.5V, t_ox=1.5nm and for t_si=5 and 10nm. Measures data [11] agree closely with the predictions of the evanescent model and the polynomial model including the ECPE at d_eff=0.25t_si.

Figure 5: DIBL parameter versus normalized position along the channel y/L.

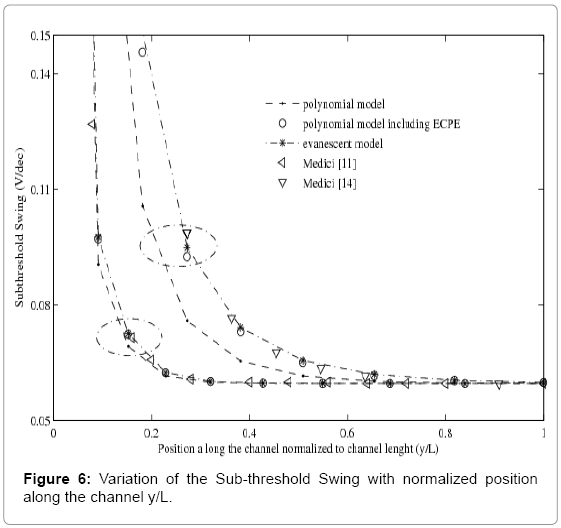
Figure 6 presents the sub-threshold swing parameter, in weak inversion, as a function of normalized position a channel length for t_ox=1.5nm, t_si=10nm, N_a=1.10¹⁷cm^-3 and V_ds=1V [11] and for t_ox=1.5nm, t_si=20nm, N_a=1.1016cm^-3 and V_ds=1V. We notice an adequate convergence, at d_eff=0.25t_si, between the evanescent model and the polynomial model including the ECPE with Jaju’s measurements [11] as well as those of MEDICI’s [14].

Figure 6: Variation of the Sub-threshold Swing with normalized position along the channel y/L.

The study of the short channel effects through the surface potential, the threshold voltage, the DIBL and the sub-threshold swing has proved the convergence situation of the evanescent model and the polynomial model including the ECPE. The convergence situation for the ultrathin SDG FD SOI MOSFET’s device is at d_eff=0.25t_si.