Short Notes on Unsupervised Learning Method with Clustering Approach forTumor Identification and Tissue Segmentation in Magnetic Resonance Brain Images
Received: 05-Dec-2015 / Accepted Date: 04-Jan-2016 / Published Date: 07-Jan-2016
Abstract
Malignant and benign types of tumor, infiltrated in human brain are diagnosed with the help of an MRI scanner. Using the slice images obtained using an MRI scanner; certain image processing techniques are implemented to have a clear anatomy of brain tissues. One such image processing technique is hybrid Self Organizing Map (SOM) with Fuzzy K Means (FKM) algorithm, which offers a possible identification of tumor region penetration in the tissues of brain. The proposed algorithm is efficient in terms of Jaccard Index, Dice Overlap Index (DOI), Sensitivity, Specificity, Peak Signal to Noise Ratio (PSNR), Mean Square Error (MSE) and Computational time and memory requirement for processing the Magnetic Resonance (MR) brain images. Automatic detection of tumor region in MR (Magnetic Resonance) brain images has a good impact in helping the radio surgeons to identify the exact topographical location of tumor region. In this paper, the proposed hybrid SOM – FKM algorithm supports the radio surgeon by providing tissue segmentation and an automated tumor identification.
Keywords: SOM (Self Organizing Map); FKM (Fuzzy K – Means algorithm); Tumor segmentation; Peak Signal to Noise Ratio (PSNR); Jaccard Index; Dice Overlap Index (DOI); Sensitivity; Specificity; Mean Square Error (MSE); Brain image segmentation and Computational time
5179Introduction
The effects created by tumor are extremely dangerous, leading to the formation of lesions and tumor within the human body. The most complicated organ of our human body is the brain and the cancer cells affecting the tissues of brain induce tumor formation [1]. Instead of manual segmentation of brain tissues and identification of tumor region, an automated algorithm capable of performing tumor identification and tissue segmentation processes is proposed through this paper.
MR (Magnetic Resonance) brain image sequences are classified as T1, T2, FLAIR (Fluid Attenuated Inversion Recovery), MPR (Multi Planar Reconstruction) and MRS (Magnetic Resonance Spectroscopy) images. T1, T2 and FLAIR image sequences are segmented by the proposed SOM – FKM algorithm.
Dr. N. Nandha Gopal [2] recommended an automatic detection of brain tumor, which is capable of producing a segmentation accuracy of 95.16%.
Govindaraj Vishnuvarthanan and Murugan Pallikonda Rajasekeran [3] recommended an automated tumor extraction and tissue segmentation using Fuzzy. It suffers in terms of high computational time and MSE along with low PSNR values.
El-Hachemi Guerrout et al [4] used Markov Random Field (MRF) Theory for medical image segmentation. The algorithm performs medical image segmentation only upon T1 – W and T1 – W Contrast Enhanced (T1-W CE) images using a Cluster of PCs.
Related Work
Ben George and Karnan [5] developed a Bacteria Foraging Optimization algorithm for segmenting MR brain images in a computational time of 31.21 seconds. Lesser computational time supports the radiologist to segment large clinical data volumes. Sultan Aljahdali et al [6] suggested an automated fuzzy rule based algorithms for reliable image segmentation. T1 – W images were segmented using both Fuzzy K – Means and Kernel Based Fuzzy C – Means algorithms. Sultan Aljahdali and Zanaty [7] proposed an automated image segmentation using modified fuzzy algorithms. Improvement of segmentation accuracy and computational speed are unavoidable in case of medical image segmentation. Somasundaram and Kalaiselvi [8] recommended an automated brain extraction algorithm for axial T2 – W images. Other modalities of MR brain image sequences could be discussed too. Vasuda and Satheesh [9] introduced an improved FCM algorithm for MR (Magnetic Resonance) brain image segmentation. Reduction of convergence rate of the proposed algorithm remains a major setback. Logeswari and Karnan [10] reported a brain tumor detection using segmentation process based on Self Organizing Maps (SOM), which is cornered to segment T2 – W image sequences. Logeswari and Karnan [11] offered a brain tumor detection using segmentation process based on Hierarchical Self Organizing Map (HSOM) technique, where T2 – W images were segmented in an average time period of 29.9708 s, which requires further minimization. Yan Li and Zheru Chi [12] performed MR brain image segmentation using SOM, wherein MSE values are to be reduced. Andac Hamamci et al [13] introduced a novel segmentation algorithm for segmenting contrast enhanced T1 – W images. Meritxell Bach Cuadra et al [14] initiated a semi – automated atlas based segmentation of MR images suffering from pathologies. Almost all the above said methodologies focus on segmenting any two sequences of MR brain images, whereas the proposed methodology endures segmentation of T1, T2 and FLAIR image sequences.
Scope of Our Work
The main aim of our methodology is to offer an entirely automated hybrid algorithm to segment the tumor region present in the brain images. An automated algorithm greatly assists the radio surgeon in the process of non – invasive diagnosis of the patients affected with tumor. Further, multimodal image sequences of a MRI scanner with all three axes namely, coronal, sagittal and axial are segmented with the support of the proposed algorithm. A radio surgeon can efficiently plan a pre and post radio therapeutic procedures using the hybrid SOM – FKM algorithm. Comparison parameters validate the performance of the algorithm and the results are compared with Fuzzy C Means (FCM) algorithm. Since, FCM and FKM are the two competitive clustering algorithms, we choose FCM as an algorithm to compare with SOM combined FKM with strategy.
Materials and Methods
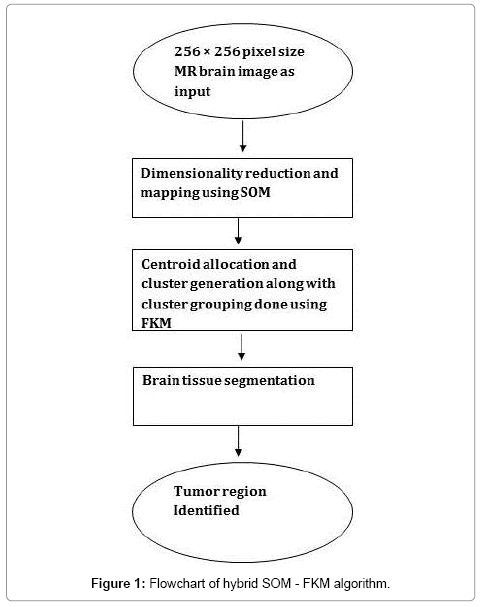
A simple flowchart explaining the sequential steps of the proposed method is given below for easy understanding (Figure 1).
Fuzzy C Means Algorithm
Fuzzy C - means (FCM) algorithm is a clustering methodology introduced by Dunn, improved by Bezdek and further spruced by Matteo Matteucci; which groups the pixels (data) of the MR brain images as ‘n’ number of clusters. The neighbouring pixel of least mean distance from the centroid pixel are defined with low membership grade value and are hierarchically grown around the centroid value. The membership grade and the cluster centers are iteratively updated to reduce the objective function of grouping the pixels.
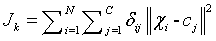 (1)
(1)
N - Number of data points given as an input.
K - Number of iterations to be performed.
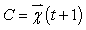 - Number of clusters into which the pixels are to be grouped.
- Number of clusters into which the pixels are to be grouped.
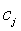 - Centre vector for the clusters (Centroid value of the pixels).
- Centre vector for the clusters (Centroid value of the pixels).
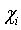 - Data points (voxels or pixels).
- Data points (voxels or pixels).
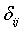 - Degree of membership for the ith data point of x_i in cluster j.
- Degree of membership for the ith data point of x_i in cluster j.
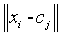 -Measuring the similarity or mean distance of the neighbouring voxels present in the data point xi to the centre vector (centroid value) of cluster j.
-Measuring the similarity or mean distance of the neighbouring voxels present in the data point xi to the centre vector (centroid value) of cluster j.
Degree of membership is given as,
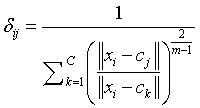 (2)
(2)
m=Fuzziness co – efficient obtained from the overlapping of clusters in a range of 1.5 ≤ m ≤ 2.5 for optimum segmentation results [15]. Centre vector (Centroid voxel) for the cluster is defined as,
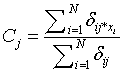 (3)
(3)
During the preliminary processing of the algorithm, 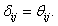 Here,
Here, 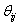 is a random value initiated as,
is a random value initiated as, 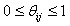 (Usually expressed as 0, 0.1, 0.2, 0.4….1), such that,
(Usually expressed as 0, 0.1, 0.2, 0.4….1), such that, 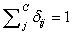
In general, FCM algorithm has higher data supervision capacity and has better processing upon diversified data range. On the other end, the convergence rate gets affected if the number of clusters and iterations are amplified. Reducing the number of iterations and clusters to obtain a better convergence rate has a negative impact upon the segmentation accuracy. To overcome these hindrances, a novel segmentation algorithm is proposed through this paper.
Fuzzy K Means Algorithm
Fuzzy K means algorithm, also called as FKM, acts an active contestant to FCM algorithm. FKM partitions the given input image into ‘k’ clusters (partitioning the pixels present in the image).
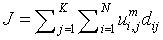 (4)
(4)
N - Data points or pixels present in the input image.
K - Number of clusters formed by FKM.
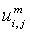 - Membership functions of FKM with fuzziness coefficient m (fuzziness co–efficient is obtained from the overlapping of clusters).
- Membership functions of FKM with fuzziness coefficient m (fuzziness co–efficient is obtained from the overlapping of clusters).
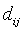 -Squared Euclidean distance between pixel Xi and cluster representative Cj (Cluster center or centroid value).
-Squared Euclidean distance between pixel Xi and cluster representative Cj (Cluster center or centroid value).
FKM algorithm has faster convergence rate and requires less operation time for processing an image. It has limitations in handling the data of wider range [16]. Taking favour of quicker convergence rate, FKM is used in the proposed methodology and the problem of data range handling is overcome using SOM.
Self-Organizing Map algorithm
The first step of processing a SOM algorithm commences with initialization, where random variables are chosen for the initial weight vectors Wj, derived from the input image. Second step involves sampling process by which an input vector X is drawn from the input image. In third step, finding the winning neuron I(x) with weight vector closest to the input vector is done (Calculation of Euclidean distance). Each point I in the output image will map to a corresponding point w(I) in the input image. In fourth step, the weight equation is updated.
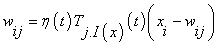 (5)
(5)
Here, Topographical neighbourhood is defined as
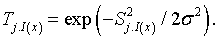 (6)
(6)
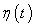 - Dependant learning rate based upon time ‘t’ for the input vector X.
- Dependant learning rate based upon time ‘t’ for the input vector X.
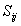 - Lateral distance between neurons i and j on the grid of neurons. The size of the neighbourhood σ needs to decrease with the time value ‘t’.
- Lateral distance between neurons i and j on the grid of neurons. The size of the neighbourhood σ needs to decrease with the time value ‘t’.
 - Connection weight between the input units i and the neurons j.
- Connection weight between the input units i and the neurons j.
Finally, the drawing of vector X from the input image is iteratively repeated until the feature map stops changing. SOM itself is a unsupervised neural network based clustering technique, which can be directly used in segmentation process [10,17].
Proposed Methodology
The combination of SOM and FKM is the main novelty proposed in this paper. SOM is used for initial clustering and reduction of dimensionality of the input image. The image given as input to the algorithm is of 256×256 dimension, which is reduced with the aid of SOM algorithm. Updated weight function Wij, [18] is the resultant value obtained using SOM. The weight function Wijis given as an input to FKM algorithm. Thus the problem aroused due to FKM in handling wide and large data range is minimized with the inclusion of SOM. Next, FKM utilizes the output from SOM and performs the clustering operation [16]. Clinical and live images of patients suffering from High grade Astrocytoma, Glioma, Prenative Neuro Ectodermal, Meningioma, Nerve sheath and Metastatic Bronchogenic Carcinoma tumors are used in this paper.
Comparison Parameters
MSE (Mean Square Error)
Mean Square Error defines the process of squaring the differentiated quantities [19]. It is expressed in Equation (6). MSE is the cumulative squared error value between the input image I (i,j) and the segmented image K (i,j).
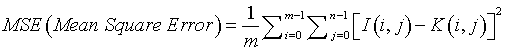 (6)
(6)
‘m’ & ‘n’ denote the number of rows and columns present in an input image.
i=m, to perform incremental operation for ‘rows’ in a loop statement.
j=n, to perform incremental operation for ‘columns’ in a loop statement.
MSE value of the resulting segmented image should be minimized. Smaller MSE values denote minimized error occurrence in the segmented MR brain images.
PSNR (Peak Signal to Noise Ratio)
Peak Signal to Noise Ratio refers to the immunity of an image to noise signals [20]. If the PSNR value is high, then the impact of noise interference signal upon the MR brain image is quite low. The algorithm producing PSNR values ranging between 40 to 100 dB is considered to be less sensitive to noise signals. PSNR is defined as:
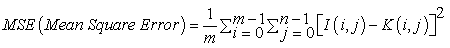 (7)
(7)
Memory Requirement
The memory space occupied by the algorithm to perform the entire segmentation process is expressed in terms of memory required. Usually, the memory requirement for a segmentation process should be as low as possible and is expressed as bytes.
Jaccard (Tanimoto) Index
Jaccard index is denoted as the ratio of the common voxels between the input image (A) and the segmented output image (B) to the union function of the input image (A) and the segmented output image (B) [16].
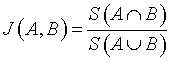 (8)
(8)
Dice Overlap Index (DOI)
DOI value is expressed using Jaccard index J (A, B). DOI specifies the overlapping function of the input image (A) and the segmented output image (B) [13].
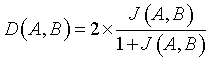 (9)
(9)
Similarity Index (SI)
Similarity Index describes the similarity between the input image (A) and the segmented output image (B) [13,21]. The values used to calculate SI are:
True Positive (TP): Correct classification of tissue region and identification of tumor region.
False Positive (FP): Normal tissue region present in the input image identified as tumor region.
False Negative (FN): Tumor region undetected or misclassified.
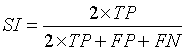 (10)
(10)
Overlap Fraction (OF)
Overlap Fraction (OF) value refers to the correct segmentation of input image. Specifically, OF defines the rate of tumor region and other tissue regions being correctly identified [13,21].
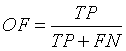 (11)
(11)
Extra Fraction (EF)
Extra Fraction (EF) refers to the number of pixels being falsely detected as tumor region and tissue regions misclassified. EF should be as low as possible [13,21].
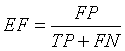 (12)
(12)
Sensitivity
The term sensitivity refers to the ability of an algorithm to classify or segment the tissues of non-tumor region [13,21].
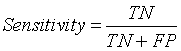 (13)
(13)
Here TN represents True Negative value. It describes the effective segmentation of non – tumor region or normal brain tissues by the algorithm.
Segmentation Results From Hybrid SOM – FKM Algorithm
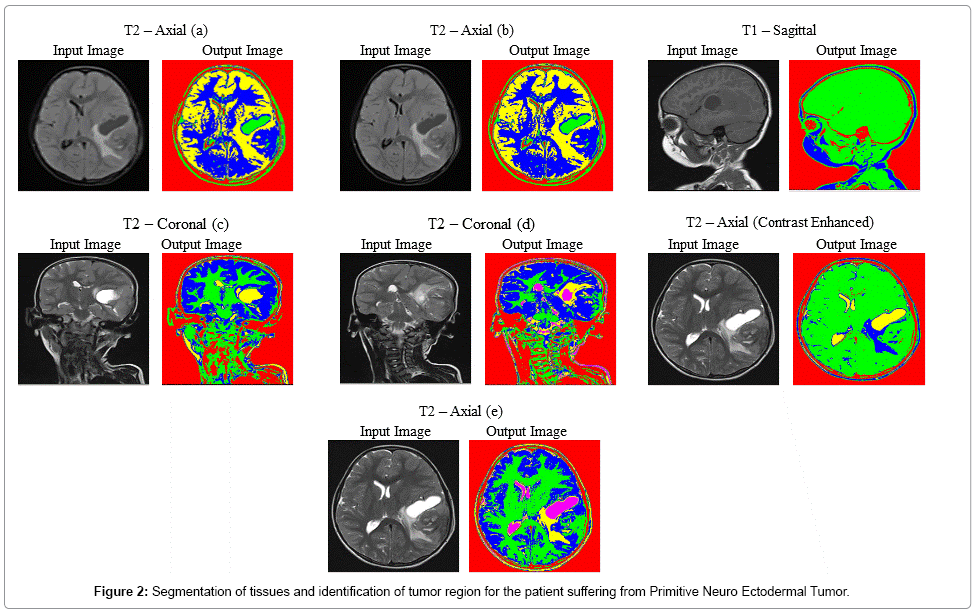
Figure 2 explicits the segmentation process of MR brain images of the patient suffering from Primitive Neuro Ectodermal Tumor, with an age of 5 years. In T2 – Coronal (d), T2 – Axial contrast enhanced and T2 – Axial (e) images, tumor and edema covered region are identified clearly. In T2 – Axial (a) and T2 – Axial (b), unique identification of tumor region is done. The average time duration required for processing the seven images of Figure 2 by SOM – FKM algorithm is 48.64 seconds and the average memory requirement is 5.31E+14 bytes.
Figure 3 demonstrates the segmentation ability of the proposed algorithm in identifying the tumor region in a challenging clinical case of age 37 years. Both T1 – coronal and T1 – Sagittal have meningioma, which is clearly identified using SOM – FKM algorithm. The challenging tumor regions and their identification are denoted by a circle region in the above images. The average time duration required for processing the two images of Fig 3 by SOM – FKM algorithm is 22.49 s and the average memory requirement is 4.66E+14 bytes.
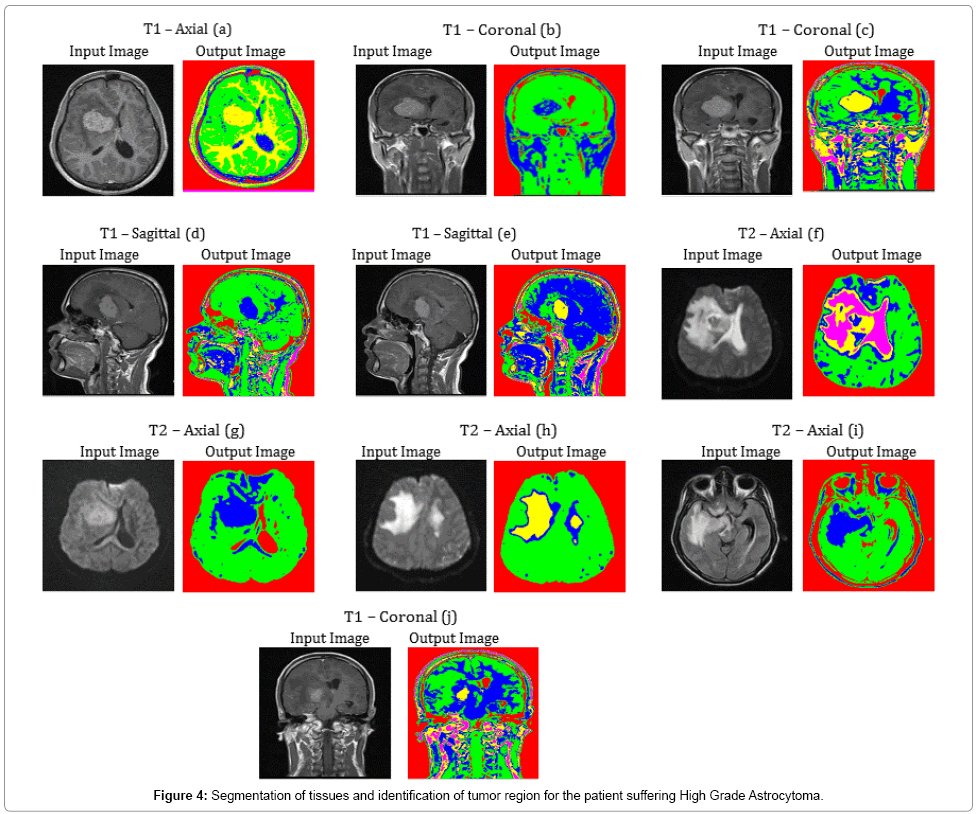
Tumor and Edema regions in T1 – Axial (a), T2 – Axial (f) and T2 – Axial (h) images of Figure 4 are clearly detected with the aid of the proposed methodolgy. Other images of Figure 4 also show the segmentation ability of SOM – FKM algorithm. During diagnosis, the age of the patient was found to be 42 years. The average time duration required for processing the ten images of Figure 4 by SOM – FKM algorithm is 19.43 s and the average memory requirement is 2.70E+14 bytes.
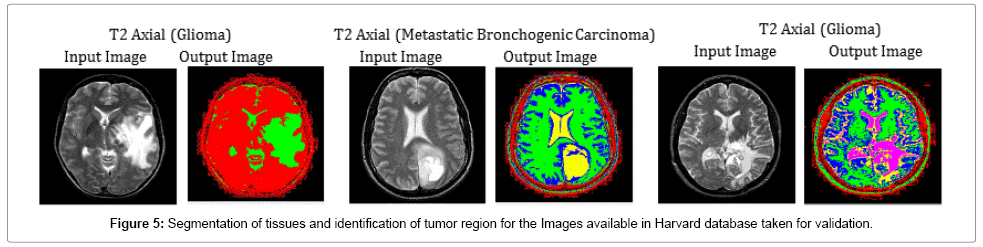
Figure 5 has been completely chosen to validate the segmentation efficiency of the hybrid SOM – FKM algorithm. Images of the patients suffering from different tumor diseases were taken from online Harvard brain repository for validating the segmentation algorithm. The average time duration required for processing the three images of Fig 5 by SOM – FKM algorithm is 11.19 s and the average memory requirement is 3.48E+14 bytes.
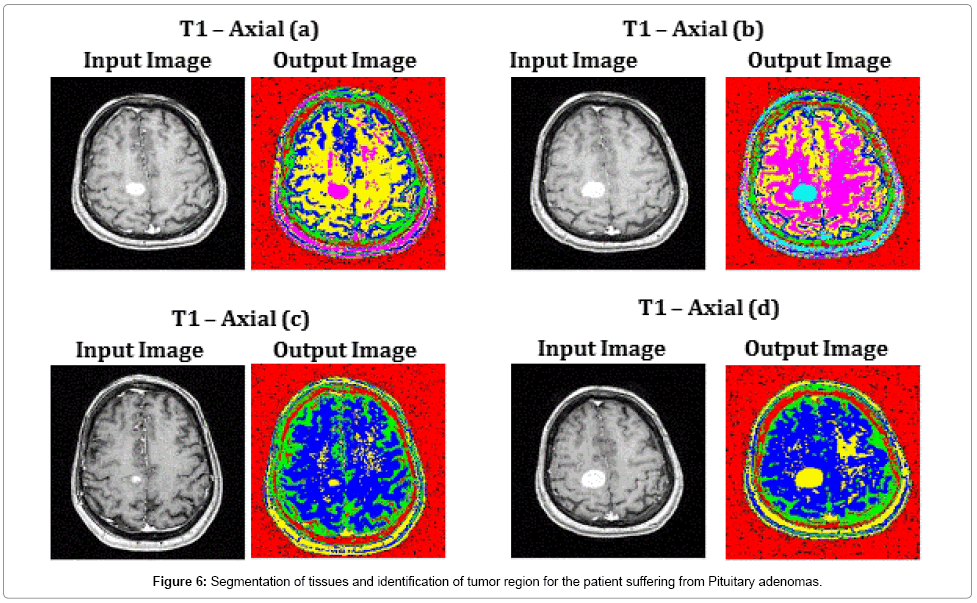
Images T1 – Axial (a), T1 – Axial (b) and T1 – Axial (d) of Figure 6, illustrate the perfect segmentation of brain tissues and clear identification of tumor region by SOM – FKM algorithm. The average time duration required for processing the four images of Figure 6 by SOM – FKM algorithm is 2.9343 s and the average memory requirement is 4.51E+13 bytes.
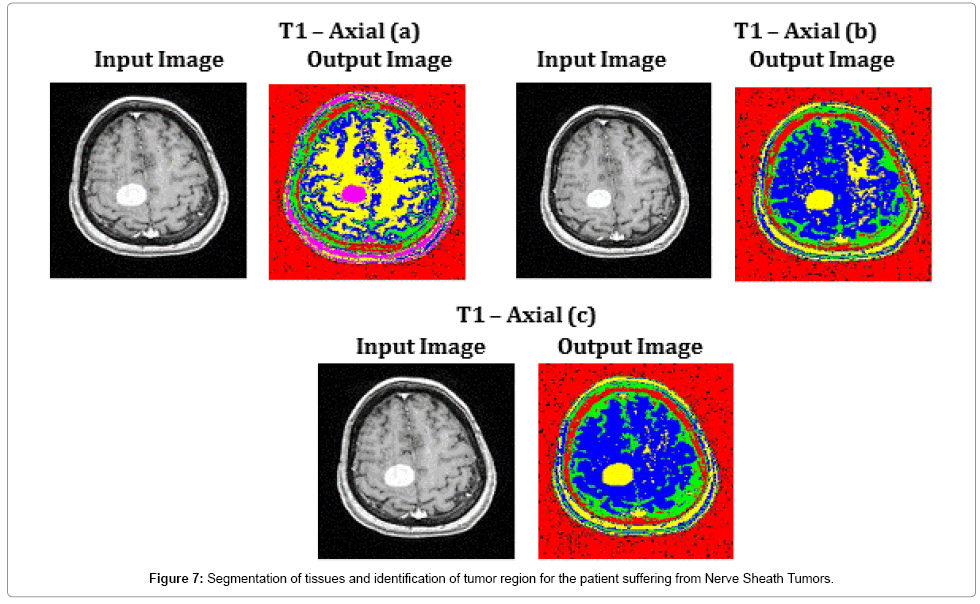
T1 – Axial (a), T1 – Axial (b) and T1 – Axial (c) of Figure 7, show the capability of the proposed algorithm in segmenting the tissue regions and exact identification of tumor region. This helps the radio surgeon to plan pre-surgical procedures. The average time duration required for processing the three images of Figure 7 by SOM – FKM algorithm is 4.2267 s and the average memory requirement is 4.23E+13 bytes.
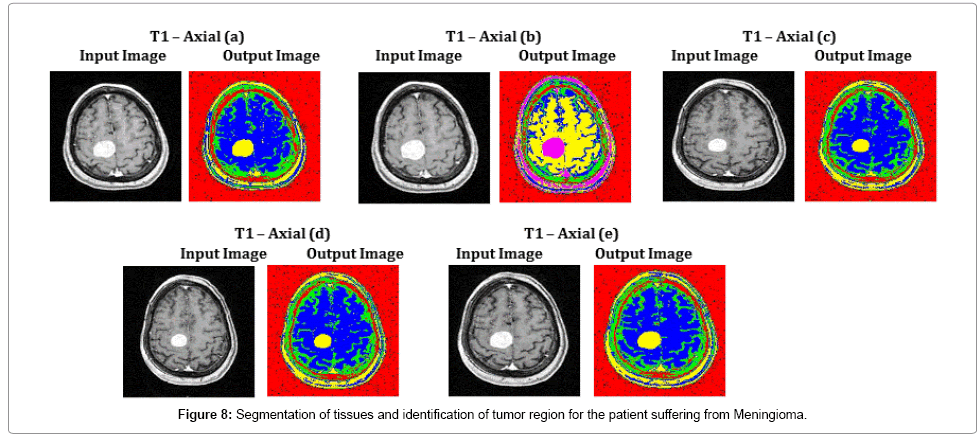
In challenging cases of Figure 8, specifically in T1 – Axial (b) and T1 – Axial (d), tissue regions are poorly captured by a MRI scanner of 1.5 Tesla. These tissue regions are clearly viewed and the tumor region is identified with the assistance of the proposed methodology. The average time duration and memory requirement required for processing the five images of Fig 8 by SOM – FKM algorithm are 3.369 s and 4.44E+13 bytes.
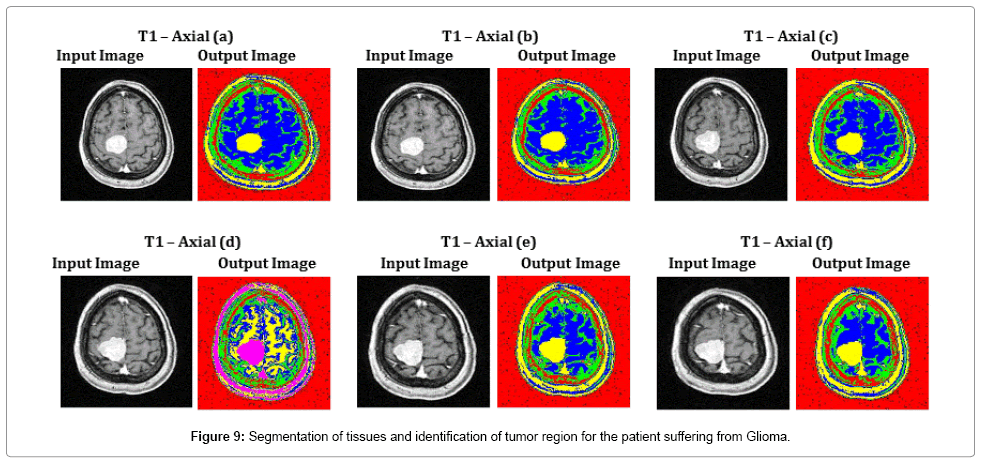
Figure 9 depicts the segmentation results of all complex T1 axial images, where the tissue regions are clearly distinguished for the better viewing of a radio surgeon. Exact segmentation of tissue region in T1 – Axial (d), proves the effectiveness of the proposed SOM – FKM algorithm. The average time duration and memory requirement required for processing the six images of Figure 9 by SOM – FKM algorithm are 3.237 s and 3.56E+13 bytes.
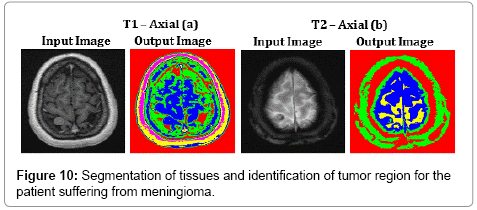
Figure 10 represents the segmentation results of the proposed algorithm. Distorted or noise affected Skull and Cerebro Spinal Fluid regions of T2 – Axial (b) image are clearly identified using SOM – FKM algorithm. The average time duration and memory requirement required for processing the two images of Figure 10 by SOM – FKM algorithm are 3.447 s and 4.54E+13 bytes.
Discussion
Table 1 shows the efficiency of the proposed algorithm in terms of MSE, PSNR, Jaccard Tanimoto Coefficient Index (TC) and DOI. The Hybrid SOM – FKM algorithm produces an average MSE value of 0.388095 on comparison with FCM algorithm, which produces an average MSE value of 2.067619. SOM – FKM outperforms FCM in terms of PSNR values. The average PSNR values produced by SOM – FKM and FCM algorithms are 58.74786 and 45.34333. The proposed algorithm also ranks higher in producing better DOI and TC values. The average DOI and TC values produced by SOM – FKM algorithm are 0.435105 and 0.282381, Whereas, FCM algorithm produces 0.412143 and 0.26881 as DOI and TC values.
| No. | Input Images | Fig. | MSE Values | PSNR Values | TC | DOI | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| FCM | SOM - FKM | FCM | SOM - FKM | FCM | SOM - FKM | FCM | SOM – FKM | |||
| 1. | T2 – Axial (a) | 2 | 1.78 | 0.77 | 45.62 | 59.67 | 0.42 | 0.48 | 0.59 | 0.6563 |
| 2. | T2 – Axial (b) | 1.77 | 0.5 | 45.62 | 60.97 | 0.42 | 0.48 | 0.59 | 0.6519 | |
| 3. | T1 – Saggital | 1.04 | 0.44 | 47.92 | 62.11 | 0.42 | 0.42 | 0.59 | 0.5996 | |
| 4. | T2 – Coronal (c) | 1.20 | 0.76 | 47.31 | 59.71 | 0.42 | 0.44 | 0.59 | 0.6129 | |
| 5. | T2 – Coronal (d) | 1.39 | 0.47 | 46.69 | 63.39 | 0.42 | 0.43 | 0.59 | 0.6091 | |
| 6. | T2 – Axial (Contrast Enhanced) | 0.99 | 0.05 | 48.15 | 72.59 | 0.42 | 0.44 | 0.59 | 0.6195 | |
| 7. | T2 – Axial (e) | 1.47 | 0.59 | 46.43 | 60.83 | 0.42 | 0.42 | 0.59 | 0.5966 | |
| 8. | T1 – Coronal | 3 | 1.01 | 0.13 | 48.04 | 67.16 | 0.42 | 0.45 | 0.59 | 0.6298 |
| 9. | T1 – Saggital | 1.54 | 0.77 | 46.24 | 59.67 | 0.42 | 0.45 | 0.59 | 0.6268 | |
| 10. | T1 – Axial (a) | 4 | 2.21 | 0.40 | 44.68 | 56.36 | 0.30 | 0.30 | 0.46 | 0.4727 |
| 11. | T1 – Coronal (b) | 2.64 | 0.66 | 43.90 | 54.18 | 0.30 | 0.30 | 0.46 | 0.4692 | |
| 12. | T1 – Coronal (c) | 2.92 | 0.16 | 43.47 | 60.22 | 0.37 | 0.32 | 0.47 | 0.4893 | |
| 13. | T1 – Saggital (d) | 1.83 | 0.15 | 45.50 | 65.05 | 0.25 | 0.26 | 0.40 | 0.4169 | |
| 14. | T1 – Saggital (e) | 3.03 | 0.10 | 43.30 | 66.92 | 0.25 | 0.25 | 0.40 | 0.4050 | |
| 15. | T2 – Axial (f) | 2.09 | 0.38 | 44.91 | 61.15 | 0.24 | 0.25 | 0.39 | 0.4087 | |
| 16. | T2 – Axial (g) | 2.86 | 0.71 | 43.56 | 58.48 | 0.24 | 0.26 | 0.39 | 0.4132 | |
| 17. | T2 – Axial (h) | 3.82 | 0.22 | 42.30 | 63.58 | 0.24 | 0.26 | 0.39 | 0.4150 | |
| 18. | T2 – Axial (i) | 2.20 | 0.52 | 44.70 | 59.81 | 0.25 | 0.35 | 0.40 | 0.5220 | |
| 19. | T1 – Coronal (j) | 1.20 | 0.81 | 47.30 | 57.95 | 0.28 | 0.35 | 0.40 | 0.5194 | |
| 20. | T2 Axial (Glioma) | 5 | 1.34 | 0.20 | 46.83 | 63.84 | 0.24 | 0.36 | 0.39 | 0.5355 |
| 21. | T2 Axial (Metastatic Bronchogenic Carcinoma) | 1.43 | 0.85 | 46.57 | 57.71 | 0.24 | 0.30 | 0.39 | 0.4660 | |
| 22. | T2 Axial (Glioma) | 0.31 | 0.12 | 53.20 | 66.14 | 0.24 | 0.23 | 0.39 | 0.3796 | |
| 23. | T1 – Axial (a) | 6 | 2.00 | 0.16 | 45.11 | 55.92 | 0.23 | 0.22 | 0.37 | 0.3638 |
| 24. | T1 – Axial (b) | 2.46 | 0.22 | 44.21 | 54.68 | 0.22 | 0.24 | 0.36 | 0.3962 | |
| 25. | T1 – Axial (c) | 2.77 | 0.05 | 43.69 | 60.42 | 0.20 | 0.20 | 0.33 | 0.3333 | |
| 26. | T1 – Axial (d) | 3.84 | 0.07 | 42.27 | 59.62 | 0.20 | 0.20 | 0.33 | 0.3333 | |
| 27. | T1 – Axial (a) | 7 | 2.12 | 0.79 | 44.84 | 49.13 | 0.20 | 0.20 | 0.33 | 0.3333 |
| 28. | T1 – Axial (b) | 4.29 | 0.71 | 41.79 | 49.64 | 0.20 | 0.20 | 0.33 | 0.3333 | |
| 29. | T1 – Axial (c) | 1.11 | 0.72 | 47.66 | 49.56 | 0.20 | 0.20 | 0.33 | 0.3333 | |
| 30. | T1 – Axial (a) | 8 | 3.03 | 0.78 | 43.31 | 49.19 | 0.20 | 0.20 | 0.33 | 0.3333 |
| 31 | T1 – Axial (b) | 1.82 | 0.09 | 45.52 | 58.31 | 0.22 | 0.20 | 0.33 | 0.3333 | |
| 32. | T1 – Axial (c) | 1.83 | 0.81 | 45.49 | 49.07 | 0.20 | 0.20 | 0.33 | 0.3333 | |
| 33. | T1 – Axial (d) | 2.68 | 0.81 | 43.84 | 49.04 | 0.20 | 0.20 | 0.33 | 0.3333 | |
| 34. | T1 – Axial (e) | 2.12 | 0.05 | 44.86 | 61.01 | 0.20 | 0.20 | 0.33 | 0.3333 | |
| 35. | T1 – Axial (a) | 9 | 2.12 | 0.06 | 44.86 | 59.77 | 0.20 | 0.20 | 0.33 | 0.3333 |
| 36. | T1 – Axial (b) | 2.08 | 0.08 | 44.94 | 58.92 | 0.20 | 0.20 | 0.33 | 0.3333 | |
| 37. | T1 – Axial (c) | 2.01 | 0.77 | 45.07 | 49.28 | 0.20 | 0.20 | 0.33 | 0.3333 | |
| 38. | T1 – Axial (d) | 2.00 | 0.07 | 45.11 | 59.24 | 0.20 | 0.20 | 0.33 | 0.3333 | |
| 39. | T1 – Axial (e) | 2.02 | 0.09 | 45.07 | 58.31 | 0.20 | 0.20 | 0.33 | 0.3333 | |
| 40. | T1 – Axial (f) | 2.71 | 0.07 | 43.79 | 59.62 | 0.20 | 0.20 | 0.33 | 0.3333 | |
| 41. | T1 – Axial (a) | 10 | 1.91 | 0.07 | 45.31 | 59.49 | 0.20 | 0.20 | 0.33 | 0.3333 |
| 42. | T2 – Axial (b) | 1.85 | 0.07 | 45.44 | 59.70 | 0.20 | 0.20 | 0.33 | 0.3333 | |
Table 1: Comparison of FCM and proposed SOM – FKM Algorithm.
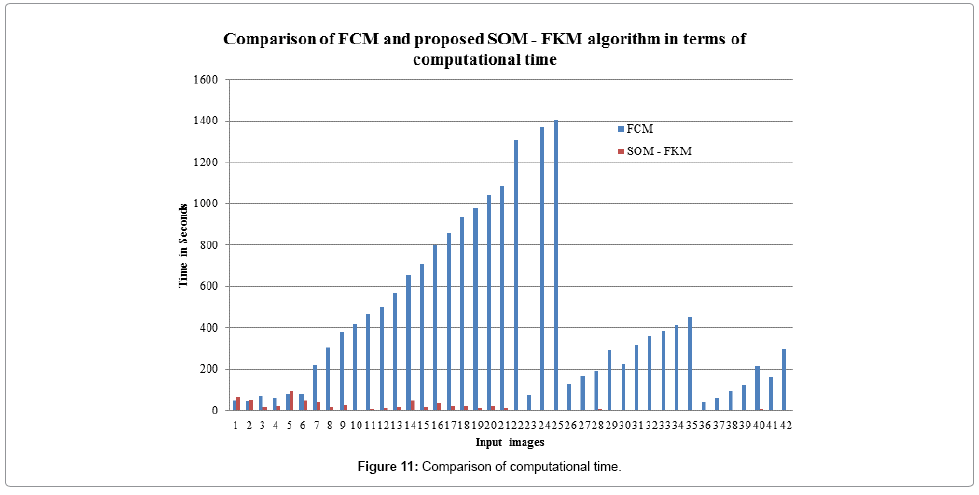
Figure 11 shows the computational time required for processing the input images by both FCM and SOM – FKM algorithms. SOM – FKM algorithm has greater efficiency in terms of computational time. The average time required for FCM algorithm to segment 42 input MR brain images is 438.1914 s, comparatively, SOM – FKM algorithm requires 16.21499 s as an average processing time.
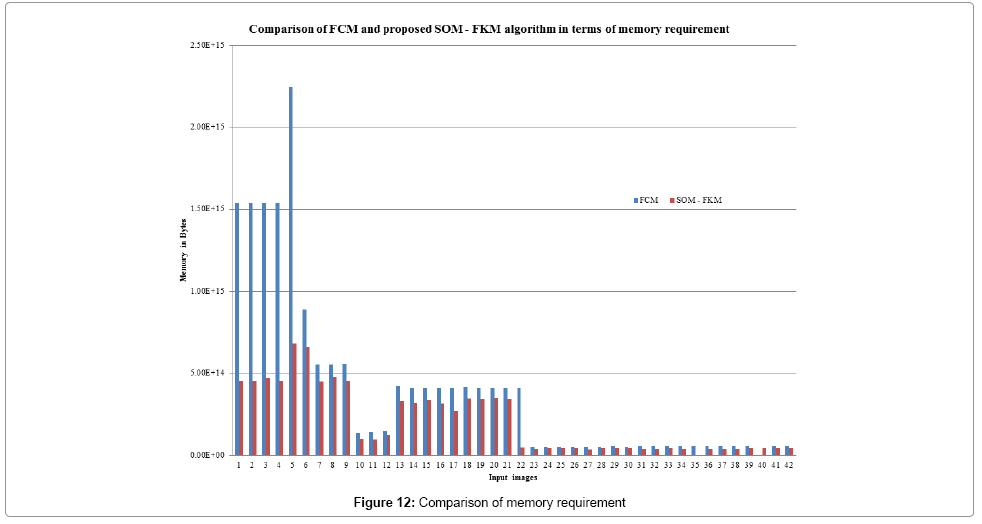
Figure 12 depicts the memory required for the algorithms to process the input images. FCM and the proposed SOM – FKM algorithms require an average memory space of 3.95E+14 MB and 2.08E+14 MB, respectively. Both the algorithms were processed on a 32 Bit operating system with Pentium 4 processor (2.2 GHz) and 2 GB RAM. Lower the memory space better is the segmentation efficiency of the algorithm.
Table 2 shows a sample of manually selected segmentation (Gold Standard) done by a clinical expert using Region of Interest (ROI) algorithm. The images of Table 2 can be compared with T2 Axial (a) of Figure 2. Using ROI, additional tissue region surrounding the tumor part has been detected as tumor, which comes under the account of false positively detected tumor region. The same set back is also observed while manually segmenting T2 – Axial (b), T2 – Coronal (d), T2 – Axial (Contrast Enhanced) and T2 – Axial (e) images of Figure 2.
 |
Table 2: A sample expert segmentation procedure for identifying tumor and edema regions.
Table 3 describes the efficiency of the proposed SOM – FKM algorithm using SI, OF, EF and Sensitivity values. The proposed algorithm overrides FCM and expert segmentation methodology by offering better SI, OF and sensitivity values. EF value is considerably reduced using SOM – FKM algorithm. For a good segmentation algorithm SI and OF value should be close to 1 and EF value should be nearer to 0 [21]. All the above said values in Table 2 make a concrete statement that the proposed hybrid SOM – FKM algorithm is superior to FCM algorithm and perform better than the expert segmentation method.
| Algorithm | Similarity Criteria | Overlap Fraction | Extra Fraction | Sensitivity |
|---|---|---|---|---|
| FCM | 0.8986 | 0.9118 | 0.1176 | 0.3333 |
| SOM - FKM | 0.9600 | 0.9474 | 0.0263 | 0.5000 |
| Expert Segmentation (Gold Standard Images) | 0.9211 | 0.9459 | 0.1081 | 0.2000 |
Table 3: Comparison of SI, OF, EF and Sensitivity values.
Conclusion
The proposed hybrid SOM – FKM algorithm excels FCM algorithm in the process of segmenting MR brain images. The effectiveness of the proposed algorithm is demonstrated using Tables 1-3. Varied clinical datasets along with standard database images have been used to prove the efficacy of the proposed algorithm. A novel automated technique to segment the tissues of brain, especially GM, WM and CSF regions, along with identification of different types of tumor at different locations has been proposed through this paper. The ultimate goal of this research work is to assist the clinician or radio surgeon in diagnosing the patients with minimized time duration and is greatly achieved through the combination of SOM and FKM techniques. Future work lies with improving the values of DOI, TC and PSNR values. Time duration for processing the images can also be further reduced. The proposed algorithm can be extensively used in pre and post radio surgical applications.
Acknowledgements
The authors thank Dr. K.G. Srinivasan, MD, RD, Consultant Radiologist and Dr. K.P. Usha Nandhini, DNB, KGS Advanced MR & CT Scan - Madurai, Tamilnadu, India, for supporting the research with the patient information and MR brain images. Also, the authors thank the Department of Instrumentation and Control Engineering of Kalasalingam University, (Kalasalingam Academy of Research and Education), Tamilnadu, India for permitting to use the computational facilities available in biomedical laboratory which was set up with the support of the Department of Science and Technology (DST), New Delhi under FIST program.
References
- ArtemMikheev, Gregory Nevsky, SiddharthGovindan, Robert Grossman, Henry Rusinek (2008) Fully Automatic Segmentation of the Brain from T1-Weighted MRI Using Bridge Burner Algorithm. Journal of Magnetic Resonance Imaging, 27: 1235-1241.
- Dr.Gopal NN (2013) Automatic Detection of Brain Tumor through Magnetic Resonance Image. International Journal of Advanced Research in Computer and Communication Engineering, Vol: 2, Issue 4.
- Govindaraj V, Murugan PR (2013) Segmentation of MR Brain Images for Tumor Extraction Using Fuzzy. International Journal on Current Medical Imaging and Reviews CMIR, 9(1).
- El-Hachemi Guerrout, Ramdane Mahiou and SamyAit-Aoudia (2013) Medical Image Segmentation on a Cluster of PCs using Markov Random Fields. International Journal of New Computer Architectures and their Applications (IJNCAA). The Society of Digital Information and Wireless Communications (SDIWC) 3(1): 35-44 (ISSN: 2220-9085).
- E Ben George and M Karnan (2012) MR Brain Image Segmentation using Bacteria Foraging Optimization Algorithm. International Journal of Engineering and Technology, Vol:4, No:5.
- Sultan Aljahdali and E A Zanaty (2012) Automatic Fuzzy Algorithms for Reliable Image Segmentation. International Journal for Computers & Their Applications, Vol. 19, No. 3.
- Sultan Aljahdali and E A Zanaty (2010) Improving Fuzzy Algorithms for Automatic Image Segmentation. IEEE, 978-1-61284-732-0/11.
- Somasundaram K, Kalaiselvi T (2010) Fully automatic brain extraction algorithm for axial T2-weighted magnetic resonance images. See comment in PubMed Commons below ComputBiol Med 40: 811-822.
- Â Vasuda P, Satheesh S (2010) Improved Fuzzy C-Means Algorithm for MR Brain Image Segmentation. (IJCSE) International Journal on Computer Science and Engineering Vol. 02, No. 05, 1713-1715.
- Logeswari T, Karnan M (2010) An improved implementation of brain tumor detection using segmentation based on soft computing. Journal of Cancer Research and Experimental Oncology Vol. 2(1). 006-014.
- Logeswari T, Karnan M (2010) An Improved Implementation of Brain Tumor Detection Using Segmentation Based on Hierarchical Self Organizing Map. International Journal of Computer Theory and Engineering, Vol. 2, No. 4, 1793-8201.
- Yan Li and Zheru Chi (2005) MR Brain Image Segmentation Based on Self-Organizing Map Network. International Journal of Information Technology Vol. 11, No. 8.
- Kohonen, Teuvo (1982)Â Self-Organized Formation of Topologically Correct Feature Maps. Biological Cybernetics 43 (1): 59-69.
- Meritxell Bach Cuadra, Claudio Pollo, Anton Bardera, Olivier Cuisenaire, Jean-Guy Villemure, et al. (2004) Atlas-Based Segmentation of Pathological MR Brain Images Using a Model of Lesion Growth.IEEE transactions on medical imaging, vol. 23, no. 10.
- Sikka K, Sinha N, Pankaj KS, Amit KM (2009) A fully automated algorithm under modified FCM framework for improved brain MR image segmentation.Magnetic Resonance Imaging 27, pp.994-1004.
- Ortiz (2013) Two fully-unsupervised methods for MR brain image segmentation using SOM-based strategies, Applied soft computing, pp.2668-2682.
- Andac H, Nadir K, Kutlay K, Kayihan E and Gozde U, (2011) Tumor-Cut: Segmentation of Brain Tumors on Contrast Enhanced MR Images for Radiosurgery Applications. IEEE transactions on medical imaging, vol. 31, pp. 3.
- Welstead and Stephen T Fractal, Wavelet image compression techniques, SPIE Publication, ISBN 978-0-8194-3503-3, p. 155-156.
- Chang CT (2011) A Fuzzy K-Means Clustering Algorithm Using Cluster Center Displacement. Journal of information science and engineering, 27, pp. 995-1009.
- Thomos N, Boulgouris NV, Strintzis MG (2006) Optimized transmission of JPEG2000 streams over wireless channels. See comment in PubMed Commons below IEEE Trans Image Process 15: 54-67.
- Khayatia R, Vafadusta M, Towhidkhaha F, Nabavi SM (2008) Fully automatic segmentation of multiple sclerosis lesions in brain MRFLAIR images using adaptive mixtures method and Markov random field model. Computers in Biology and Medicine, 38, 379- 390.
Citation: Govindaraj V, Vishnuvarthanan A, Thiagarajan A, Kannan M, Murugan PR (2016) Short Notes on Unsupervised Learning Method with Clustering Approach for Tumor Identification and Tissue Segmentation in Magnetic Resonance Brain Images. J Clin Exp Neuroimmunol 1:101.
Copyright: ©2016 Govindaraj V, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Select your language of interest to view the total content in your interested language
Share This Article
Recommended Journals
Open Access Journals
Article Usage
- Total views: 13876
- [From(publication date): 3-2016 - Aug 16, 2025]
- Breakdown by view type
- HTML page views: 12900
- PDF downloads: 976