Research Article Open Access
Statistical Analysis of Sea Surface Temperature and Chlorophyll-a Concentration Patterns in the Gulf of Tadjourah (Djibouti)
Youssouf MO1,2*, Laurent M2 and Xavier C3
1Centre for Study and Research in Djibouti Airport Road, PO Box 486, Djibouti
2UMR6539 UBO/CNRS/IRD/Ifremer European University Institute of the Sea (IUEM) Technopole Brest Iroise, 29280 Plouzane, France
3University of Western Brittany (UBO) UMR 6523 CNRS/IFREMER/UBO Physics Laboratory of the Ocean, IUEM, Plouzané, France
- *Corresponding Author:
- Youssouf MO
Centre for Study and Research in Djibouti Airport Road
PO Box 486, Djibouti
Tel: + 25377262108
E-mail: assoum_omar42@yahoo.fr
Received Date: January 14, 2016; Accepted Date: February 29, 2016; Published Date: March 07, 2016
Citation: Youssouf MO, Laurent M, Xavier C (2016) Statistical Analysis of Sea Surface Temperature and Chlorophyll-a Concentration Patterns in the Gulf of Tadjourah (Djibouti). J Marine Sci Res Dev 6:186. doi: 10.4172/2155-9910.1000186
Copyright: © 2016 Youssouf MO, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Journal of Marine Science: Research & Development
Abstract
The sea surface temperature (SST) and chlorophyll-a concentration (CHL-a) were analysed in the Gulf of Tadjourah from two set of 8-day composite satellite data, respectively from 2008 to 2012 and from 2005 to 2011. A singular spectrum analysis (SSA) shows that the annual cycle of SST is strong (74.3% of variance) and consists of warming (April-October) and cooling (November-March) of about 2.5C than the long-term average. The semi-annual cycle captures only 14.6% of temperature variance and emphasises the drop of SST during July-August. Similarly, the annual cycle of CHL-a (29.7% of variance) depicts high CHL-a from June to October and low concentration from November to May. In addition, the first spatial empirical orthogonal function (EOF) of SST (93% of variance) shows that the seasonal warming/cooling is in phase across the whole study area but the southeastern part always remaining warmer or cooler. In contrast to the SST, the first EOF of CHL-a (54.1% of variance) indicates the continental shelf in phase opposition with the offshore area in winter during which the CHL-a remains sequestrated in the coastal area particularly in the south-east and in the Ghoubet Al-Kharab Bay. Inversely during summer, higher CHL-a quantities appear in the offshore waters. In order to investigate processes generating these patterns, a multichannel spectrum analysis was applied to a set of oceanic (SST, CHL-a) and atmospheric parameters (wind speed, air temperature and air specific humidity). This analysis shows that the SST is well correlated to the atmospheric parameters at an annual scale. The windowed cross correlation indicates that this correlation is significant only from October to May. During this period, the warming was related to the solar heating of the surface water when the wind is low (April-May and October) while the cooling (November-March) was linked to the strong and cold North-East winds and to convective mixing. The summer drop in SST followed by a peak of CHL-a, seems strongly correlated to the upwelling. The second EOF modes of SST and CHL-a explain respectively 1.3% and 5% of the variance and show an east-west gradient during winter that is reversed during summer. This work showed that the seasonal signals have a wide spatial influence and dominate the variability of the SST and CHL-a while the east-west gradient are specific for the Gulf of Tadjourah and seem induced by the local wind modulated by the topography.
Keywords
Sea surface temperature; Chlorophyll a concentration; Singular spectrum analysis; Empirical orthogonal function; Multichannel singular spectrum
Introduction
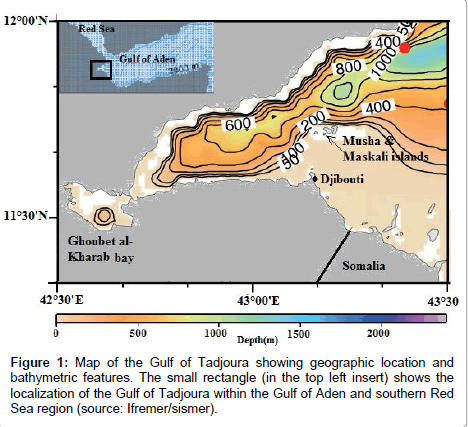
The Gulf of Tadjourah (GOT) extends from the Gulf of Aden and penetrates deep into the Horn of Africa (Figure 1). It is almost completely surrounded by the Djibouti land masses, except for the south eastern portion which prolongs into Somalia. This semi-enclosed sea has specific geomorphological features that distinguish it from the Gulf of Aden. In the south-east, the continental shelf is wider and includes two islands (Moucha and Maskali) and many sandbanks are scattered throughout the entrance of the GOT. In the North, the GOT is crossed by a large rift (Tadjourah rift) extending westward toward the Ghoubet El Kharab Bay and the Assal Lake (150 m below sea level), one the hottest and most volcanically active areas in the world [1,2].
The extreme climate conditions of the Afar depression and the arid lands surrounding the GOT seem to have an important impact on the water properties, in particular on surface temperature and salinity. The volcanic formations in the west may also enhance marine primary production by providing minerals such as iron. On the oceanic side, GOT is located on the confluence of the Red Sea and the Indian Ocean. The climate is mainly governed by the Indian Ocean monsoon regime; alternation of North-Eastern and South-Western monsoon winds regulates surface circulation. Given these aspects, the GOT constitutes a unique marine ecosystem with many ill-understood but remarkable phenomena.
From an economic perspective, the GOT includes most of the exclusive economic zone of Djibouti (EEZD) and provides almost all local fish resources. The coastal area also provides seafood and services to the inhabitants of the surrounding arid lands. These resources could be affected by changes in physical and biogeochemical properties due to the global warming [3,4]. It is therefore important to establish a fishing policy that is based upon scientific knowledge of the ecosystem and its exploitation potential. Surprisingly, very little information is available on oceanographic conditions and bio-productivity of the GOT. The area has been very little studied.
The few data available come from research ships passing through Djibouti. In the pioneering study and using merchant ships, Donguy, 1970, 1972 and 1974 [5-7] collected data on sea surface temperature, salinity and wind speed between Djibouti port and Cap Guardefui. Limited to the Eastern part of the GOT, these data indicate the existence of two marine seasons. The highest temperatures were observed between March and May in the offshore waters of Djibouti and the lowest ones from November to February. Subsequently, some descriptive ecological studies provide limited data on climatic and oceanographic conditions of the GOT. In 1974-1976, Perez and Braud [8] collected data on temperature, turbidity and wind speed around the Moucha and Maskali Islands. These data showed that from January to April, surface water temperatures remain stable and spatially homogenous (24-26C). However, from May to November, temperatures show high frequency oscillations and are spatially heterogeneous. Robineau and Rose [9] reported that temperatures fluctuate between 25C during winter and 29°C during summer.
However, there is very limited information on primary production of the GOT. The descriptive works [10,11] on fish assessment relate the summer abundance of pelagic fish to the phytoplankton bloom. More recently, as part of the monitoring of the quality of the coastal water, Awaleh et al. [12] collected data on 26 stations located close to Djibouti city. During this survey, very low chlorophyll a concentrations (0.006 to 0.06 μg/l) were observed at sampling sites. On a regional scale, the Gulf of Aden is considered as an oligotrophic area during summer, with a surface chlorophyll bloom which only occurs during winter due to deep convective mixing [13,14].
Understanding surface patterns of temperature and primary production is of great importance, particularly when looking at their implications for the ecosystem and the influences on the local fisheries. Unfortunately, the above referenced large-scale studies in the Gulf of Aden are spatially limited. The descriptive studies at a local small scale are restricted to certain areas or are temporally sporadic. They do not provide a synoptic and clear picture of the variability of the two parameters as they evolve throughout the year.
The present work aims to improve the understanding of the changes in thermal structure and primary production and their patterns of temporal and spatial variability in the GOT. As this study is essentially based on a statistical approach, the robust statistical analysis methods, as well the techniques to separate signal and noise through decomposition are briefly described. Results focus on the most important modes of variability of two studied parameters (SST and CHL-a). The relationship between these two parameters and also the link with atmospheric parameters is studied through covariance analysis.
Data and Methodology
Data
The challenge was to find satellite data with the same temporal and spatial resolutions for SST and CHL-a, in our study area. Subsequently, the two parameters were first studied separately, using data at different spatial resolutions and over different periods. The purpose here is to decompose data and identify the mean patterns of variability for each parameter.
Data on sea surface temperature
SST AVHRR_MetopA: For temporal and spatial variability analysis, we used the daily SST derived from the METOP/Advanced Very High Resolution Radiometer (AVHRR) for the period January 2008 to December 2012. These data were provided by the CERSAT (Centre ERS d’Archivage et de Traitement - French ERS Processing and Archiving Facility) at IFREMER (Institut français de Recherche et d’exploitation de la mer). The data have spatial resolution of 0.05°× 0.05° which corresponds to approximately to 16 grid points in latitude direction and 20 grids points in longitude direction for the GOT, so we have 16×20 grid points and 225 observations (2008-2012), at each grid point to describe the state of GOT SST. Details on this product can be found in [15,16]. The validation of data for July 2007 to December 2013 at a global scale was made using the Matchup Data Base and also by comparison with data from the other sensors [17]. This indicates a negligible error of - 0.05 K and a standard deviation of 0.48 K for night time data against 0.9 K and 0.58 K for daytime data [18]. We used in this study only the night time data. To test the validity of these data in our area of study, we used in situ daily collected data using a temperature-conductivity sensor (Hobo U24) at near-surface (2 m depth) in the Gulf of Tadjourah from April to July 2013. The comparison of the SST AVHRR_MetopA daily-averaged data in the vicinity of the temperature-conductivity sensor showed that the two data evolve linearly during this short period. The mean difference was estimated at 0.6°C.
Ocean colour data: The CHL-a distribution in the GOT was analysed using the merged ocean colour product (Chlorophyll-a, case I water: CHL1) from the Moderate Resolution Imaging Spectroradiometer (MODIS) and Medium Resolution Imaging Spectrometer (MERIS) with a 1 km by 1 km resolution. These data are 8-day composites and were provided by GlobColour/ST-ACRI (see: http://hermes.acri.fr/) from 2005 to 2011. Thus, in our area of study, the data consist of 81×61 grid points and 303 observations at each grid point.
Atmospheric parameter data: Atmospheric parameters data were reprocessed from “Daily Turbulent Flux” product provided by CERSAT/Ifremer. This product contains daily data on turbulent flux air temperature (Tair), specific air humidity (Qa10), and wind speed (W10) and also the sea surface temperature (SST). The data are gridded over the global ocean at a spatial resolution of 0.25° by 0.25° [19]. They cannot be used alone to analyse spatial variability in the GOT because of their low resolution. Therefore, the limited grid points were averaged to perform time series from 2005 to 2009 in order to analyse the relationship between SST, CHL-a and the atmospheric parameters.
Methodology
Pre-processing: As shown in Figure 1, the study area of study is limited between 42°30E – 43°30E and 11°20N – 12°00N. We have extracted a set of satellite images for this area for the above described products of SST and CHL-a. The daily data for SST were first transformed to 8-day composites by simple averaging over the entire area of study. This transformation has allowed the reduction of missing data and to provide with have the same temporal resolution as the CHL-data. For the latter, as the chlorophyll-a concentration is approximately log normally distributed in nature [20] a logarithmic scale (base 10) was used.
Temporal variability analysis: For each field, from each image, “sea pixels” were retrieved using land masking. Then time series was performed through a simple averaging of the “sea pixels” of each image. These time series can be presented as shown in (1): X is a time dependent physical variable, t is the equally spaced record time and N: the length of the sample. The objective here is to separate signals from noise as showed in (2). This was done using singular spectrum analysis decomposition.
Xm (t) = xt, xt+1, xt+2, ……xn (1)
X(t) = Signal(t) + ε (t) (2)
Singular spectrum analysis (SSA): SSA is designed to extract useful information from short and noisy time series [21]. In simple terms, the SSA method can be visualised as a sliding window of length M, moving down a time series X(t) of length N. SSA decomposes time series into eigenvectors or temporal EOFs. The projection of these EOFs on the original time series yield temporal principal components or PCs Each PCs captures a type of variation representing trend, periodic oscillations, and structure less variations or noises [22-26].
Separability, identification and grouping of the temporal principal components: Following decomposition, the resulting additive components (PCs) must be separated and identified. This is firstly based on eigenvalues spectrum inspection. Thus, the oscillatory component is generally characterised by a pair of nearby equal eigenvalues and the associated PCs are in phase quadrature. After identification, the entire time series, or parts of it that correspond to trends, oscillatory modes or noise, can be reconstructed by linear combinations of the PCs and EOFs, providing the reconstructed components (RCs). The dependence between RCs is measured using the weighted correlation (See [21] for the calculation of w-correlation matrix). The main steps of the SSA method are described in detail in [27,28]. Here, the Caterpillar SSA 3.4 software, (available at http://www.gistagroup.com, see also [29]) was used to implement all steps of computation. The window length (M) determination is a critical step of the SSA method. The choice of this parameter impacts SSA results directly, and can be a source of numerical noise [30]. To determine this parameter, we first applied a simple spectral analysis to the time series in order to find the main period (T). Then, as recommended by [27], M was set as a multiple of this period, but less than a third of the length of the time series (M = kT; M< N/3). Furthermore, we have tested different values of M, and the root mean square error (RMSE) – between the original time series and the reconstructed ones was computed for each case. Thus, the value of M that corresponds to the lowest RMSE is retained.
Monte Carlo SSA test: As mentioned above, selection of the RCs are empirically based on the SSA reparability theory [27]. Unfortunately, this approach is limited in the presence of the autocorrelation. As pointed out in reference [31], the interdependence between observations introduces red noise that could lead to RCs with high ranks in the eigenspectrum. In order to identify either the oscillatory components associated with red noise or to objectively separate signal from noise, the Monte Carlo SSA (MC-SSA) was applied against the null hypothesis H∅: data are derived from red noise, in particular autocorrelation at lag 1 or AR(1). This was done using simulated realisations (surrogate data) and the comparison of their eigenspectrum with the eigenvalues of the original data. The test is performed in three main steps:
1- The surrogate data were generated from original data using linear autoregressive model (AR1).
Xt = aXt-1 + εt (3)
2- Then, the covariance matrix (C) is computed from all surrogate data. This matrix is projected onto the eigenvalue basis (EX) of the original data (4).
ΛR = EtxCEx (4)
3- The comparison between the given surrogate data and the original data is quantified by computing the values of the discriminating statistics (confidence interval) of the diagonal elements of ΛR via Monte Carlo simulation. The null hypothesis is rejected where the eigenvalue falls outside the red noise confidence interval [31].
Harmonic analysis: Harmonic analysis aims to decompose periodic time dependent data into a sum of sinusoidal functions. Here, this method was applied to supplement SSA analysis in order to isolate and clearly define periodic components in SST and CHL-a time series. From a discrete data set (1), a periodogram was obtained using Fast Fourier Transform (Matlab fft). From the periodogram, the fundamental frequency (ω0) is determined graphically. Then, the Fourier coefficients An and Bn were estimated by integrating equations (6) and (7) between zero and the fundamental period T. The amplitude and phase of each harmonic were calculated using equations 8 and 9.
F(t)= Ancos(nω0t)+Bnsin(nω0t) (5)
 (6)
(6)
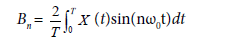 (7)
(7)
 (8)
(8)
 (9)
(9)
Empirical orthogonal analysis: While the SSA technique is suitable for one-dimensional time series analysis, empirical orthogonal function (EOF) is helpful in identifying spatial components (spatially uncorrelated) varying in time [32,33]. The EOF analysis was applied to a set of 8-day composites images of SST and CHL-a, after the long-term average was removed from each grid point (10).
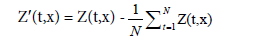 (10)
(10)
CE = En(x)λi (11)
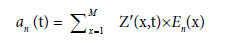 (12)
(12)
The resulting anomalies Z′(t,x) are then decomposed through eigenanalysis (or diagonalisation). This produced the eigenvectors En and eigenvalues (λi) as shown in (11). The temporal coefficients an (t) are obtained by projecting data on the associated eigenvectors. The an (t) represent amplitudes of the eigenvector at each sampling time t. To facilitate physical interpretation, an(x) were normalised to unit variance and regressed against the original data set. This makes it possible to obtain regression maps (EOFn) in the same units as the initial data. In addition, individual EOF must be evaluated for uniqueness. Following [34], it is possible to assign a “standard error” δλ, to each eigenvalue. This error depends on the size of sample N or, more precisely, on the number of effective independent samples N′ (13): the total number of observations reduced by the autocorrelation time scale (Tscale) as in (14). The latter is estimated from ACF (autocorrelation functions) using the formula proposed by Thomson et al. [35].
 (13)
(13)
N′ = N/Tscale (14)
 (15)
(15)
One mode (i) is considered significant if the error δλi of its associated eigenvalue λi is smaller than the distance Δλi between λi and its nearest eigenvalue.
Multichannel singular spectrum analysis: Multichannel spectrum analysis (M-SSA) is an extension of the SSA method (described in section 2.2.3) adapted to more than one time series or channel. The aim of the M-SSA is to isolate and distinguish patterns of similar temporal behaviour [36]. Here, in order to extract oscillatory and persistent common modes, the M-SSA is first applied to a trajectory matrix of normalised 8-day time series of all the oceanic and atmospheric parameters.
Results
Temporal variability
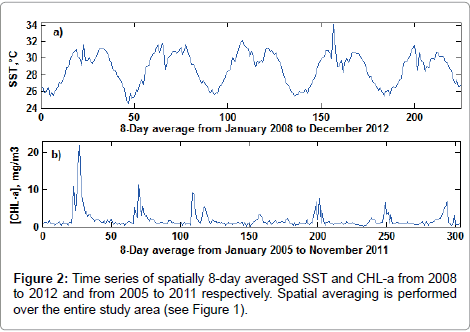
SST: Figures 2a and 2b shows the spatially 8-day averaged SST from January 2008 to December 2012. From this time series, the annual cycle is discernible. The average SST varies from a minimum of approximately 25-26°C between December and February to a maximum of 31-32C achieved in May and September. Between these two maxima, a sharp drop during July-August was discerned.
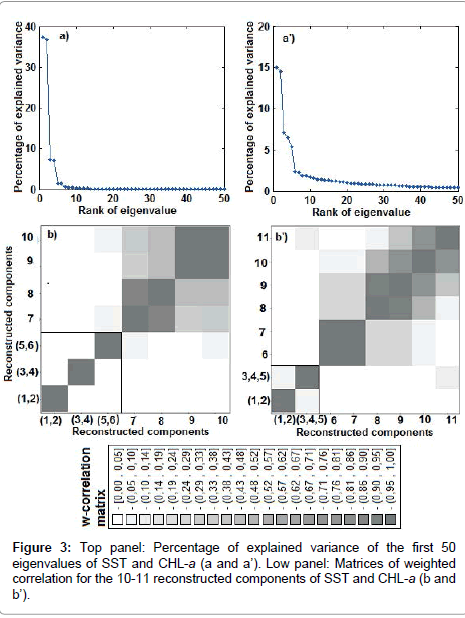
Choosing M (window length = 90) and performing SSA decomposition of the trajectory matrix, provided us with 90 eigenvalues, of which the first 50 are shown in Figure 3a. The first two pairs of eigenvalue (ranks 1 to 4) are well separated from the remainder. The plotting of the related eigenvectors (not shown here) indicates periodic components from rank 1 to 6. From rank 7, eigenvalues are very close and asymptomatically linear. The highly correlated components (rank 1-2, rank 3-4 and rank 5-6) were grouped to perform the three first RCs (Figure 3b).
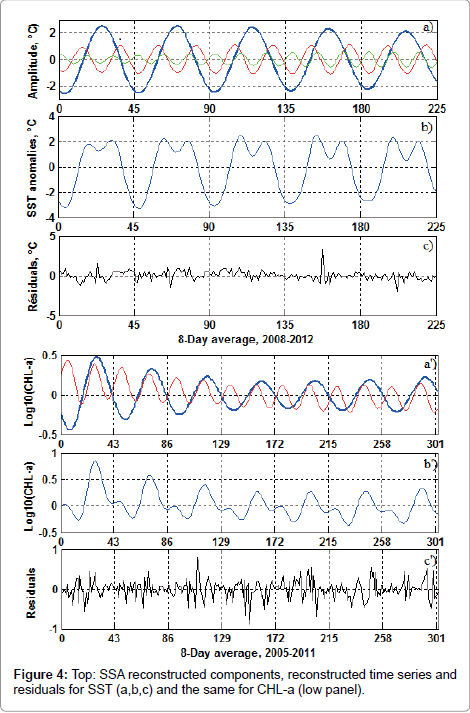
The first RCs (Figure 4a, thick blue line) accounts for 74.3% of the total variance and show an increase in temperature from March to May-June, followed by a decrease until December. The second RCs (red line) account for 14.6% of the variance and emphasises the drop in temperature in July. The third component (green line) accounts only for 3% and shows three maxima and minima of low amplitudes (Figure 4b). The reconstructed time series from the three RCs contribute at about 91.9% of temperature variance. The RMSE between the original and the reconstructed time series remains low (RMSE ≈ 0.79). The residuals (Figure 4c) have no apparent signal but indicate the extrema, particularly in 2008 and 2011.
CHL-a: The spatially 8-day averaged CHL-a is illustrated in Figure 2b. This time series is characterised by a pronounced and amplitude variable peak occurring every year in July-August. During the rest of the year, CHL-a remains low. The SSA decomposition (window length M=86) of logarithm (base 10) of the CHL-a results in 86 eigenvalues whose first 50 are shown in Figure 3a). The first pair and the three following eigenvalues are well separated. The first RCs corresponding to the first pair of eigenvalues (blue thick line) cover 29.7% of variance and present a maximum in July-August (Figure 4a). The second RCs associated with the three eigenvalues (rank 3, 4 and 5) explain 19% of the variance and indicate a first peak in February-March and a second in July-August (Figure 4a). The reconstructed time series from these two RCs (Figure 4b) fit well with the original time series (RMSE= 0.22).
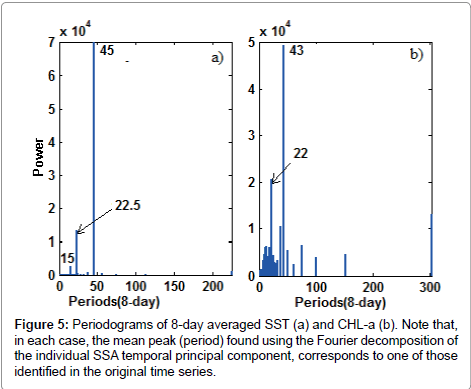
To characterise the cyclic components described above, spectral analysis based on Fast Fourier Transform (FFT) was applied to the original time series of SST and CHL-a. This resulted in three peaks of 45, 22.5 and 15, 8-day cycle (360, 180 and 120 days) for SST (Figure 5a) and two peaks of 43 and 22, 8-day cycle (344 and 176 days) for CHL-a (Figure 5b). The same analysis applied to each SSA isolated RCs of SST and CHL-a shows identical periods. This means that the three RCs correspond to annual, semi-annual and four month cycles in SST time series and the annual and semi-annual cycles in CHL-a time series. Note that for CHL-a, in addition to two mean periods (43 and 22 8-day cycles), the spectrum indicates several shorter periods. The amplitude and phase of each harmonic were calculated using equations 6, 7, 8 and 9.
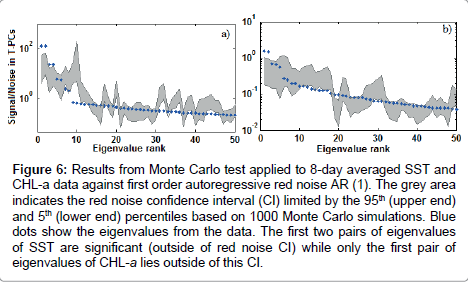
The results of the Monte Carlo test applied to two time series of SST and CHL-a are illustrated in Figure 6. In the case of SST (Figure 6a), the first two pairs of eigenvalues are outside of the confidence interval (CI) of AR (1). Therefore, the first and second RCs associated with these two pair eigenvalues are considered as significant at 95%. While for the CHL-a, only the first pair of eigenvalues associated to the first RCs lie outside the CI (Figure 6b). Therefore, the annual and semi-annual cycle for SST but only the annual cycle for CHL-a are statistically significant. The equations 16 and 17, represent the results of Fourier decomposition applied to the SST and CHL-a times series.
Figure 6: Results from Monte Carlo test applied to 8-day averaged SST and CHL-a data against first order autoregressive red noise AR (1). The grey area indicates the red noise confidence interval (CI) limited by the 95th (upper end) and 5th (lower end) percentiles based on 1000 Monte Carlo simulations. Blue dots show the eigenvalues from the data. The first two pairs of eigenvalues of SST are significant (outside of red noise CI) while only the first pair of eigenvalues of CHL-a lies outside of this CI.
 (16)
(16)
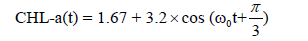 (17)
(17)
EOF mode description
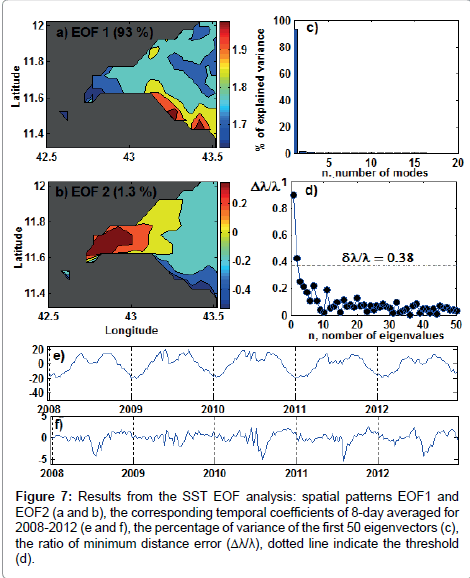
Figures 7a-7e shows the eigenvalue spectrum of the first 50 eigenvalues for SST. Following the North et al. criterion, only the two first eigenvalues exceed the 95% confidence error (Figure 7d). The first EOF mode of SST explains 93% of the variance. Its spatial pattern is in phase and positive across the whole study area (the amplitudes of the spatial EOF corresponding to the amplitudes in the real data). The noticeable feature of this spatial map is that the South-East remains warmer and the Western relatively cooler. However, as the temporal coefficient a1(t) changes signs and becomes negative from November to March, the inverse spatial pattern occurs : the product EOF1×a1(t) is negative across the gulf, the southeast remaining cooler (Figures 7a-7e). The spectral analysis of a1(t) shows a strong peak, with a period of 44 8-day (352 days), and a second one of 22 8-day (176 days). This indicates that the first EOF mode represents a combination of annual and semi-annual cycle variations of SST. The second EOF mode accounts only for 1.3% of the variance and clearly indicates a westward gradient. The eastern part remains positive and the western negative when the temporal coefficient a2(t) is positive (November-December). This pattern is reversed when a2(t) becomes negative from May to September (Figures 7b and 7f).
Figure 7: Results from the SST EOF analysis: spatial patterns EOF1 and EOF2 (a and b), the corresponding temporal coefficients of 8-day averaged for 2008-2012 (e and f), the percentage of variance of the first 50 eigenvectors (c), the ratio of minimum distance error (Δλ/λ), dotted line indicate the threshold (d).
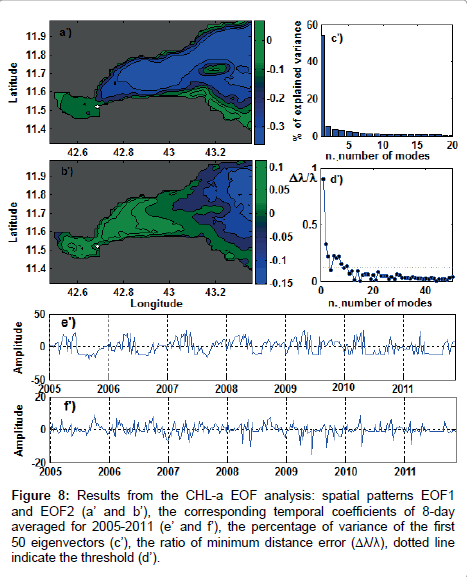
For the CHL-a field, the first seven eigenvalues, with the exception of rank 4, exceed the confidence error (Figures 8a-8e). From these EOF modes, we selected only the first two with a higher percentage of explained variance. The first mode of CHL-a explains 54.1% of the variance and its spatial map shows positive amplitude in the coastal area and negative on the offshore area. This pattern occurs from January to May when the temporal coefficient is positive. From June to September, the temporal coefficient becomes negative, so the EOF1×a1(t) becomes positive in the offshore area and negative in the coastal area (Figures 8a-8e). Similarly to the SST, the spectral analysis of the temporal coefficient shows two periodic components corresponding to annual and semiannual cycles (Figure 8e). The second mode accounts for 5.2% of the variance and shows a westward gradient in phase opposition occurring in March and August when the temporal coefficient is positive, but varying from one year to another (Figure 8f).
Figure 8: Results from the CHL-a EOF analysis: spatial patterns EOF1 and EOF2 (a’ and b’), the corresponding temporal coefficients of 8-day averaged for 2005-2011 (e’ and f’), the percentage of variance of the first 50 eigenvectors (c’), the ratio of minimum distance error (Δλ/λ), dotted line indicate the threshold (d’).
To check whether the spatial patterns of EOF change depending on the area, the study area was expanded eastward to 44°N and northward to 14°N, including the west of the Gulf of Aden and the southern Red Sea. The results of the EOF analysis shows that the first EOF modes are similar, while the second modes are significantly different from those identified in the GOT. In the case of the CHL-a, we note also that the amplitude of the spatial EOF is greater in the west of the Gulf of Aden than in the Gulf of Tadjourah. The south Red Sea appears to display very low CHL-a compared to the west of the Gulf of Aden.
SST and CHL-a variability related to atmospheric parameters
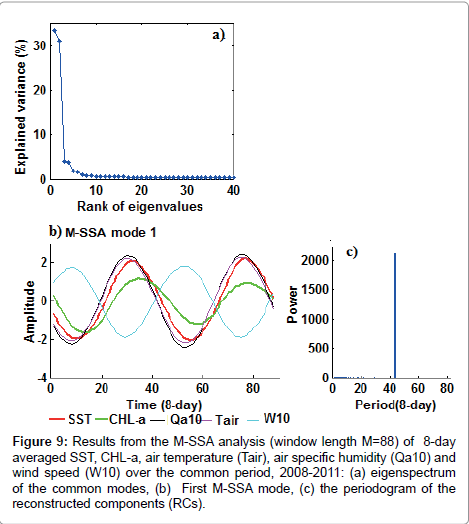
The M-SSA was applied to analyse the relationship of the SST and CHL-a with the atmospheric parameters, in particular air temperature (Tair), specific air humidity (Qa10) and wind speed (W10). The results of the M-SSA analysis are presented in Figure 9. As shown on the eigenvalue spectrum (Figure 9a), the first pair of eigenvalues is well separated. The second pair is close to the asymptomatically linear eigenvalues. Based on the breaking of the slope in the spectrum of eigenvalues (“Screen test”, see [37]), only the first M-SSA mode associated with the first pair of eigenvalue is considered significant. The associated components (SST, CHL-a, Tair, Qa10 and W10) of this first M-SSA mode depicts a single peak at 44 8-Day cycle, which correspond to the annual cycle (Figure 9). The annual cycle of SST is highly and positively correlated with Tair and Qa10 but negatively correlated with wind speed (Table 1). The CHL-a shows low correlation with all the atmospheric parameters. These results reveal that the annual cycle is the most significant common signal linking the SST to the atmospheric parameters. To examine whether this relationship varies according to the time of the year, the correlation between SST, CHL-a with atmospheric parameters was estimated separately for each four month period: window 1: February-May (FMAM), window 2: June-September (JJAS) and window 3: October-January (ONDJ). This indicates that SST remains highly correlated to the atmospheric parameters only during the first and the third windows, corresponding to the period extending from October to May. No significant correlation was detected for the second window which corresponds to the summer period (June- September). The CHL-a does not correlate with any atmospheric parameter during any of the three periods (Table 2).
| Mode 1 (M-SSA) | ||||
| r (0 lag) | rmax | phase | Dt(jours) | |
| SST/Tair | 0.97 | 0.99(-1) | -0.26 | 15 |
| SST/Qa10 | 0.97 | 0.99(-1) | -0.27 | 16 |
| SST/W10 | -0.94 | -0.99(-2) | 2.79 | 157 |
| CHL-a/Tair | 0.79 | 0.96(-4) | -0.59 | 33 |
| CHL-a/Qa10 | 0.79 | 0.97(-4) | -0.59 | 33 |
| CHL-a/W10 | -0.74 | -0.96(-5) | 2.46 | 138 |
Table 1: Results from the multichannel singular spectrum analysis (M-SSA) showing the correlation and phases between components.
| Time series | Window 1 (FMAM) | Window 2 (JJAS) | Window 3 (ONDJ) |
| SST/Tair | 0.85 | 0.08 | 0.88 |
| SST/Qa10 | 0.85 | 0.56 | 0.94 |
| SST/W10 | -0.4 | 0.05 | -0.8 |
| CHL-a/Tair | -0.19 | 0.14 | 0.92 |
| CHL-a/Qa10 | -0.33 | -0.33 | 0.95 |
| CHL-a/W10 | -0.14 | -0.26 | -0.84 |
Table 2: Results of a windowed cross-correlation using a window length of 120 days (four months) between two ensembles of oceanic and atmospheric parameters.
Figure 9: Results from the M-SSA analysis (window length M=88) of 8-day averaged SST, CHL-a, air temperature (Tair), air specific humidity (Qa10) and wind speed (W10) over the common period, 2008-2011: (a) eigenspectrum of the common modes, (b) First M-SSA mode, (c) the periodogram of the reconstructed components (RCs).
How are SST variations linked to the atmospheric influences?
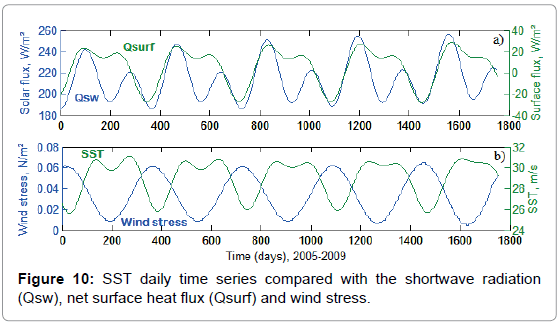
In order to analyse how the atmosphere influences the SST variation, we first computed the shortwave radiation (Qsw), longwave radiation (Qlw), latent and sensible heat flux (Ql and Qs) using daily ECMWF re-analysis data (ERA-40 interim) averaged for the study area. The net heat flux at the surface (Qsurf) was estimated by the sum of radiative flux and turbulent flux. The evolution of Qsw and Qsurf is compared to the time series of SST and wind stress time series from 2005 to 2009. As shown in Figure 10, the SST and Qsurf vary similarly; both time series show a drop during the summer period. To investigate the atmospheric influences on the SST variation more objectively, we used the Frankignoul method [38]. This method is based on the fact that the surface heat flux contributes to generate SST anomalies but it also affect their evolution after they have been generated, thereby acting as a feedback. As showed by [38], the surface heat flux anomalies can be decomposed as in Equation. (18).
Qsurf(τ) = q(τ) - α SST (18)
Where q is independent of the SST anomalies; -α SST is the Qsurf induced by the SST anomalies. From Equation. (18), the cross-covariance between Qsurf and SST is given by:
CovQsurf/SST(τ) = Covq/SST(τ) - α CovSST/SST(τ) (19)
Covq/SST (τ) vanishes at large negative lag (τ > 1 month). So, the feedback of the surface heat flux is estimated using the cross-covariance between SST and Qsurf, divided by the autocovariance of the SST (20).
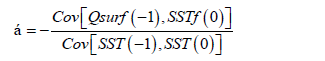 (20)
(20)
Here, α is estimated for each three consecutive monthly anomalies. For example, α during July-August-September is estimated by correlating Qsurf (JAS) with SST during June-July-August (JJA). The results are presented in Table 3. This indicates negative α from October to March so the surface heat flux feedback is positive (see Equation. 18). During this period, the ocean responses to the cooling by releasing heat to the atmosphere. From April to June, α remains high and positive; the feedback is negative. The atmosphere act by heating sea surface which storage energy. During summer (JAS), α is low, the atmosphere has less influence on the SST anomalies.
| Feedback factor (α) | JFM | AMJ | JAS | OND |
| α | -3 | 5.6 | 2.1 | -3.4 |
Table 3: Estimated atmospheric heat flux feedback factor (α) over the Gulf of Tadjoura. For each three month, α in W/m2/°C, is estimated using consecutive three months of daily data of the net heat flux (Qsurf) and the sea surface temperature (SST) time series.
Discussion and Conclusions
In this paper, one-dimensional times series of SST and CHL-a were decomposed into a sum of temporal principal components using both singular spectrum and harmonic analysis. The results of these analyses submitted to the Monte Carlo test showed that the annual and semiannual cycles for SST and only the annual cycle for CHL-a represent the most important statistically significant signals for the temporal variability of these two parameters.
The annual cycle of SST (1st harmonic) relates warming and cooling of surface waters throughout the year. These annual variations are related to the atmospheric influences. The warming of water is induced by solar heating. Indeed, the shortwave radiation flux (Qsw) increases from March to May and achieves its maximum in May-June (Figure 10a). During the same period, the SST, Tair and Qa10 increase together and achieve their maximum during the same period (May-June). However, the wind speed decreases and shows a minimum in May. This indicates that during a low wind period, solar heating induces a rise in air and sea surface temperature. The phase lag between SST and Tair could be explained by the difference in inertia between air and sea water. The increase in the specific humidity is due to the evaporation induced by the increase of SST. However, the cooling from September onward seems to be related exclusively to the strengthening of the northeast wind and the convective mixing of surface water. These prominent atmospheric influences on the annual variation of SST are consistent with the result of the surface heat flux feedback.
The spatial map of the first EOF indicates that this warming/ cooling affects the entire study area. The relative difference of the southeast area, which remains warmer during summer and cooler during winter, seems to be related to the topographic features; this area is the shallowest of the Gulf (Figure 1). The remainder of the thermal variation is almost totally represented by cooling during summer, especially in July, that appears in the second SSA reconstructed component (semi-annual cycle). Both M-SSA analysis and windowed correlation analysis showed no significant correlation between the SST and atmospheric parameters at a semi-annual scale. This indicates that the drop of SST during July-August is not related to direct atmospheric influences. The low value of the retroaction coefficient (α) confirms this hypothesis.
The annual variation of the CHL-a is characterised by low CHL-a during the majority of the year and high CHL-a during the short period from July to September. The EOF analysis indicates that during the first period, the CHL-a shows a landward gradient with the CHL-a concentrated in the coastal waters and in the Bay of Ghoubet al-Kharab. This pattern is reversed during summer, when the CHL-a increases in the offshore water and diminishes on the continental shelf. The winter pattern of the CHL-a, limited to the coastal area seems to be related to tidal mixing. However, the summer pattern of the CHL-a represented by the strong peak is most likely due to the enrichment induced by upwelling. Furthermore, the singular value decomposition (not shown), applied to the SST and CHL-a fields together, indicates that the summer “offshore water enrichment” is associated with the “summer cooling” affecting the western part of the gulf, while the “winter cooling” is associated with shelf enrichment.
This process is well recognised in the west of the Gulf of Aden, where the upper ocean is mixed and the thermocline weakens during the summer period [39,40]. The shoaling of the thermocline is due to Ekman pumping, enhanced by the strong southeast monsoon wind [41-43]. This result in surface upwelling in certain areas, particularly at the southern part of the Bal-el-Mandeb strait [44]. In the Gulf of Tadjourah, as highlighted by the spatial structure of the EOF, the upwelling seems strengthening at the extreme west of the gulf.
Our study has shown that the temporal variation in SST could be described only by the first two harmonics. In the case of CHL-a, only the annual cycle appears as a prominent and statistically significant signal of the CHL-a variance. We propose a simple statistical model from theses harmonics to represent and predict seasonal variations in SST and CHL-a. These leading patterns were identified in for the first time in the Gulf of Tadjourah and are important for understanding how thermal structure and primary production-estimated through ocean colour-evolve in this area, but also on a larger regional scale. The EOF analysis expanded on a sub-regional scale, including the west of the Gulf of Aden, limited at 44°E and southern Red Sea below 14°N, shows the same first EOF patterns (Appendix 1). In addition, our results can be compared to some existing findings for the Gulf of Aden. For instance, the annual profile of SST found by [45] for the Gulf of Aden is comparable with our reconstructed time series. The strong summer peak highlighted by the annual cycle is also consistent with results from recent work [46] that revealed that the Gulf of Aden exhibits a prominent summer chlorophyll bloom and sustains elevated chlorophyll concentrations during autumn. This indicates that the SST and CHL-a patterns, isolated in the GOT, reflects what is happening regionally, particularly in the west of the Gulf of Aden.
In contrast, the second EOF modes of SST and CHL-a, which describe only 1.3% and 5.2% of variance respectively, seems specific to the Gulf of Tadjourah [47]. They highlight a westward gradient of both SST and CHL-a; these patterns seem to be related to the local wind modulated by the orography. Nevertheless, based on the satellite data of the surface water, we are limited to the basic physical process generating the isolated leading patterns [48]. Therefore, in situ measurement in the water column waters is required for a better understanding of the mechanisms that govern the thermal structures and primary production in this particular area of the Horn of Africa.
Acknowledgements
This work was supported financially by the “Service de cooperation et d’action culturelle” of the French Embassy in Djibouti and by the government of Djibouti. We are grateful to Dr Jalludin and Dr Abdulrahman for their support and encouragement during this study. Many thanks to Dr Guillaume Maze (LPO), and to the IUEM IT team (Emmanuel Tabouret, Alain Lemercier, Camille Marzeyer) and Nasser Djama for their technical assistance. We acknowledge Dr Abderrahim Bentamy and François Piollé (Ifremer/Cersat) and also Phillippe Garnesson and Olivier Sardou (Globcolour/ACRI-ST), for providing us with the satellite data.
References
- Bosworth W, Huchon P, McClay K (2005) The Red Sea and Gulf of Aden basins. Journal of African Earth Sciences 43: 334-378.
- Bonatti E, Cipriani A, Lupi L (2015) The Red Sea: birth of ocean. In The Red Sea: The Formation, Morphology, Oceanography and Environment of a young ocean basin.
- Doney SC, Ruckelshaus M, Duffy JE, Barry JP, Chan F, et al. (2012) Climate Change Impacts on Marine Ecosystems. Annual Review of MarineScience4: 11-37.
- Levitus S, Antonov JI, Boyer TP, Baranova OK, Garcia HE, et al. (2012) World Ocean heat content and thermosteric sea level change (0-2000 m) 1955-2010. GeophysRes Lett 39: L10603.
- Donguy JR (1970) Surface observations along the shipping lines in the partWest IndianOcean. CahOckznogr 22 : 353-366.
- Donguy JR (1972) Surface data comparisonwiththose of artificial satellites in the western part of the IndianOcean. Cah O.R.S.T.O.M., sér.Océunogr X: 99-104.
- Donguy JR (1974) A year of surface observations in the monsoon zone ofwestern part of the IndianOcean. Cah. O.R.S.T.O.M., sér. Océanogr. XII: 117-128.
- Perez R, et J-PBraud (1978) Possibility of a culture of the industrialsearch rouge EucheumaSpinusum in the Gulf of Tadjourah. Science et Pêche Bull Inst Pêches marit 285.
- Robineau D, Rose JM (1982) The dugong [ Dugongdugong ( Müller, 1776) Sirenia , Dugongidae ] in Djibouti. Biological Conservation 24: 233-238.
- Bouhlel M (1988) Poissons de Djibouti. RDA International, Inc. Placerville, CA 95667, Etats-Unis.416 pages.
- Künzel T, Darar A, Vakily JM (1996) Composition, Biomasses et Possibilitésd'Exploitation des Ressources Halieutiques Djiboutiennes. Tome 2 Données. Ministère del'Agriculture et de l'Hydraulique, Djibouti / GTZ, Allemagne. 114.
- Awaleh MO, Hoch FB, Okieh BH, Ahmed SI, Soubaneh YD,et al. (2015) Impact of Human Activity on Marine and Coastal Environment in the Gulf of Tadjourah. J Marine Sci Res Dev 5: 2-11.
- Van Couwelaar M (1997) Zooplankton and micronekton biomass off Somalia and in the southern Red Sea during the SW monsoon of 1992 and the NE monsoon of 1993. Deep-Sea Research Part II-Topical Studies in Oceanography 44: 1213-1234.
- Almogi-Labina A, Schmiedl G, Hemleben C, Siman-Tov R, Segl M, et al. (2000) The influence of the NE winter monsoon on productivity changes in the Gulf of Aden, NW Arabian Sea, during the last 530 ka as recorded by foraminifera. Marine Micropaleontology 40: 295-319.
- Le Borgne P, Legendre G, Marsouin A, Péré S (2008) Operational SST retrieval from METOP/AVHRR, Validation Report.
- Eastwood S, Andersen S (2007) Masking of Sea Ice for METOP SST retrieval. OSI.
- Merchant CJ, Le Borgne P, Roquet H, Marsouin A (2009B) Sea surface temperature from a geostationary satellite by optimal estimation. Remote Sensing of Environment 113: 445-457.
- Marsouin A, Le Borgne P, Legendre G,Péré S (2010) Homogeneous validation scheme of the OSI SAF Sea surface temperature products, proceedings of the 2010 EUMETSAT conference, Cordoba, Spain, September 2010.
- Bentamy A, Grodsky SA, Katsaros K, Mestas-NunezAM(2013) Improvement in air-sea flux estimates derived from satellite observations. International Journal of Remote Sensing 34: 5243-5261.
- Campbell J (1995) The lognormal distribution as a model for bio-optical variability in the sea. J Geophys Res 100: 13237-13254.
- Hassani H (2007) Singular Spectrum Analysis: Methodology and Comparison. Journal of Data Science. 5: 239-257.
- BroomheadDS, King GP (1986a) "Extracting qualitative dynamics fromexperimental data", Physica D,20: 217-236.
- Broomhead DS, King GP (1986b) "On the qualitative analysis of experimentaldynamical systems". Nonlinear Phenomena and Chaos, Sarkar S (Ed.), Adam Hilger, Bristol pp: 113-144.
- Fraedrich K (1986) Estimating dimensions of weather and climate attractors. J AtmosSci43: 419-432.
- Vautard R, Ghil M (1989) "Singular spectrum analysis in nonlinear dynamics, with applications to paleoclimatic time series".Physica D 35: 395-424.
- Vautard R, Yiou P, M Ghil (1992) "Singular-spectrum analysis: A toolkit for short, noisy chaotic signals", Physica D 58: 95-126.
- Golyandina N, Nekrutkin V, and Zhigljavsky A (2001) Analysis of Time Series Structure: SSA and related techniques.
- Golyandina N, Zhigljavsky A (2013) Singular Spectrum Analysis for time series. Springer Briefs in Statistics, Springer.
- Golyandina N, Osipov E (2007) "The ‘Caterpillar’-SSA method for analysis of time series with missing values".J Stat Plan Inference 137: 2642-2653.
- Hassani H, Mahmoudvand R (2013) Multivariate Singular Spectrum Analysis: A General View and New Vector Forecasting Approach. Int J Energy Stat 1: 55-83.
- Allen M, Smith LA (1996) Monte Carlo SSA: Detecting irregular oscillations in the Presence of coloured noise.J Clim93373-3404.
- Venegas SA, Mysak LA, Straub DN(1997) Atmosphere–ocean coupled variability in the South Atlantic. J Climate10: 2904-2920.
- Von Storch H, Zwiers FW (1999) Statistical Analysis in Climate Research. Cambridge University Press, 494.
- North GR, Bell TL, Cahalan RF, Moeng FJ (1982) Sampling error in the estimation of empirical orthogonal functions. MonWea Rev 110:699-706.
- Thomson RE and Emery WJ (2014) Data analysis methods in physical oceanography. Newnes.
- Zotov LV (2012) Application of multichannel singular spectrum analysis to geophysical fields and astronomical images. Advances in Astronomy and Space Physics 2: 82-84.
- Cattell RB (1966) The screen test for the number of factors. Multivariate Behavioral Research 1: 245-276.
- Frankignoul C, Czaja A, L Heveder B (1998) Air-sea feedback in the North Atlantic and surface boundary conditions for ocean models. J Clim 11: 2310-2324.
- Aiki H, Takahashi K, Yamagata T (2006) The Red Sea outflow regulated by the Indian monsoon. Continental Shelf Research 26: 1448-1468.
- Al Saafani MA, ShenoiSSC (2006) Seasonal and interannual variability of eddy field and surface circulation in the Gulf of Aden.
- Bauer S, Hitchcock GL, Olson DB (1991) Influence of monsoonally-forced Ekman dynamics upon surface layer depth and plankton biomass distribution in the Arabian Sea. Deep-Sea Research 38: 531-553.
- Smith SL, Codispoti LA, Morrison JM, Barber RT (1998) The 1994–1996 Arabian Sea Expedition: an integrated, interdisciplinary investigation of the response of the northwestern Indian Ocean to monsoonal forcing. Deep-Sea Research 45: 1905-1915.
- Vecchi GA, Xie SP, Fischer AS (2004) Ocean–atmosphere covariability in the western Arabian Sea. J Climate 17: 1213-1224.
- Baars MA, Schalk PH, Veldhuis MJW (1998) In: Sherman K, Okemwa EN, Ntiba MJ (eds.) Seasonal fluctuations in plankton biomass and productivity in the ecosystems of the Somali Current. Gulf of Aden and Southern Red Sea. Large Marine Ecosystems of the Indian Ocean – Assessment, Sustainability and Management. Blackwell Science, Cambridge, U.S. 143-174.
- Nandkeolyar (2013) Comparative Analysis of Sea Surface Temperature Pattern in the Eastern and Western Gulfs of Arabian Sea and the Red Sea in Recent Past Using Satellite Data.
- Yao F, Hoteit I (2015) Thermocline regulated seasonal evolution of surface chlorophyll in the Gulf of Aden. PLOS One 10: e0119951.
- European Satellites Agency: The European Service for Ocean Colour.
- Gista T Group: Caterpillar-SSA: Time series analysis and forecasting.
Relevant Topics
- Algal Blooms
- Blue Carbon Sequestration
- Brackish Water
- Catfish
- Coral Bleaching
- Coral Reefs
- Deep Sea Fish
- Deep Sea Mining
- Ichthyoplankton
- Mangrove Ecosystem
- Marine Engineering
- Marine Fisheries
- Marine Mammal Research
- Marine Microbiome Analysis
- Marine Pollution
- Marine Reptiles
- Marine Science
- Ocean Currents
- Photoendosymbiosis
- Reef Biology
- Sea Food
- Sea Grass
- Sea Transportation
- Seaweed
Recommended Journals
Article Tools
Article Usage
- Total views: 13159
- [From(publication date):
April-2016 - Aug 18, 2025] - Breakdown by view type
- HTML page views : 11937
- PDF downloads : 1222