Research Article Open Access
Daily Variation Law of Solar Radiation Flux Density Incident on the Horizontal Surface
Zhongsheng Guo*
Institute of Soil and Water Conservation, Northwest AF University, Chinese Academy of Science, P.R. China
- *Corresponding Author:
- Zhongsheng Guo
Institute of Soil and Water Conservation
Northwest AF University, Chinese Academy of Science
Xinong Road 26, Yangling, Shaanxi Province, 712100, P.R. China
Tel: 862987012411
E-mail: zhongshenguo@sohu.com
Received date: March 31, 2017; Accepted date: August 20, 2017; Published date: August 26, 2017
Citation: Guo Z (2017) Daily Variation Law of Solar Radiation Flux Density Incident on the Horizontal Surface. J Earth Sci Clim Change 8: 412. doi: 10.4172/2157-7617.1000412
Copyright: © 2017 Guo Z. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Journal of Earth Science & Climatic Change
Abstract
The instantaneous solar radiation flux density incident on the horizontal surface near the ground, consisted of three sections, direct radiation, scattered radiation, and thermal radiation flowing down through the atmosphere, directly or indirectly comes from the sun. The dynamics of the solar radiation flux density incident on the horizontal surface near the ground influence all life processes and environment. In this study, the daily variation law of solar radiation flux density incident on the horizontal surface developed. The results showed that generally, sky conditions is stable, and the daily dynamic in the solar radiation flux density incident on the horizontal surface near the ground is the function of time, and can be described by a normal distribution model in a day. The main parameters of the model change with date and the meteorological conditions in a day.
Keywords
Horizontal surface; Solar radiation; Flux density; Hour; Sky conditions; Daily variation law; Diurnal total solar energy; Environment
Introduction
Solar energy is one of the cleanest forms of energy sources [1,2] and the main energy resource for all of the life processes, and the basic condition causing varied physical phenomenon and processes in the atmosphere. The reciprocity between solar energy and life system were generalized by photosynthesis, thermal effect, and photomorphogenesic effects [3]. Solar radiation incident on the horizontal surface comes either directly or indirectly from sun. It is this energy that makes photosynthesis possible. It provides the heat to warm the air and the soil to the levels that promote the life processes, which in turn influences the soil energy status and water evaporation [3,4]. It is significance to master the daily variation law of solar radiation flux density incident on the horizontal surface for such research and application fields as architecture, industry, agriculture, environment, hydrology, agrology, meteorology, limnology, oceanography and ecology.
Solar energy is the main energy resource used for plant transpiration and soil evaporation. For this reason, a crops growth rate, under conditions where nutrients and water is enough to support plant growth, can largely be explained by the ability of the crop to intercept and use radiation [3,5-7], and biomass production of forest stands is correlated with the capacity of stands to intercept light [8-10].
Several models have been developed to estimate the amount of global solar radiation on horizontal surfaces using various climatic parameters, such as sunshine duration, cloud cover, humidity, maximum and minimum ambient temperatures, and wind speed [2,11]. Wu et al. [12] used the metrological data from 1994 to 2005 of Nanchang station, China to predict daily global solar radiation from sunshine hours, air temperature, total precipitation and dew point. Buluta and Büyükalaca [13] proposed a simple model for estimation of monthly average of daily global solar radiation on horizontal surface for 68 provinces of Turkey with a high accuracy. Janjai et al. [14] proposed a model for calculating the monthly average hourly global radiation in the tropics with high aerosol load using satellite data. This model was employed to generate hourly solar radiation maps in Thailand [14]. But there is not a better model to express the daily variation law in solar radiation, that is to say, the relationship between time (hour) and solar radiation flux density incident on the horizontal ground. Hence studies of the daily variation law in solar radiation is very important for explaining the dynamic mechanism of environmental factors such as daily variation of temperature and humidity, plant life processes such as the daily variation of photosynthetic rate, transpiration rate, and soil physical property, for example, soil temperature.
The amount of sunlight incident on a horizontal surface just outside the earth's atmosphere (Si) is given
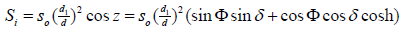 (1)
(1)
Here, S0 is the solar constant, the ratio (d1 /d)2 is varies throughout the year, from 1.0344 on 3 Jan. to 0.9674 on 5 July, but is never more than 3.5% away from 1.0, and d1 is the mean distance from the earth to the sun, which is a constant in a given place and d is the instantaneous distance at time, t, from the earth to the sun, which changes with time (day) in a year. z is solar zenith angle, and δ is the declination of the sun, and h is the hour angle of sun (angular distance from meridian of observer). ω is angle rate of the earth moving in its orbit around the sun, and the value of ω is equal to π/12 (radian) per hour, t is time. Φ is the latitude of observer
When the solar radiation passes through the earth’s atmosphere, the solar energy is dramatically reduced and dissipated in many ways. Part of the energy is reflected and part absorbed by the atmosphere, by clouds and other masses of solid particles in the atmosphere, then by the vegetation, and finally by the earth itself. The greater the distance of atmosphere through which the sun's radiation must pass, the higher the percentage of the solar radiation that is absorbed or scattered by the atmosphere particals and not received on the earth's surface. As the solar energy is dissipated, the radiation wavelengths are changed. The shorter ultraviolet rays are almost completely absorbed by the atmosphere. The radiation with wavelengths ranging from approximately 0.4 to 0.7 μ (photosynthetic active radiation) is visible to the unaided human eye and is termed light and accounts for approximately one-half of the total solar energy reaching the earth's surface. When the sun is low on the horizon, therefore, very little ultraviolet radiation reaches the surface, and more infrared radiation reaches the earth than light. The solar radiation reaching the horizontal surface is composed of three terms, direct radiation, scattered radiation, and infrared radiation or longwave radiation. The direct radiation and scattered radiation only exist in the day, and the long-wave radiation exists 24 hours period of a day [15,16].
Solar radiation influences air, leaf, and soil temperature, therefore affect the life processes of plants and animals. Recently many daily changes in solar radiation reaching horizontal surfaces of the earth have been measured [17-19]. Many resources indicated that the daily changing curve of solar radiation with time is a single peaked curve with symmetry about solar noon. However, few models have been put forward to describe quantitatively the daily change of solar radiation [20-22]. The objective of this study is to continuously measure the total solar radiation flux density incident on the ground with high-preciouse equaipment to obtain the quantitative characteristics of the diurnal solar radiation distribution and develop an Equation to describe daily variation law of solar radiation flux density and estimate the total solar energy.
Materials and Methods
Study area and station
The current study site is located on Hilly and gully region of Loess Plateau in the north region of China. There are fragile environment and long-term drought on the Loess Plateau.
The data used in this work was measured at Changwu Experimental Station under the China Academy of Sciences and Ministry of water Resources. It located at the juncture of Shaanxi Province and Gansu Province in the south part of Loess Plateau, China and launched in 1984. The geographic coordinate is N35°12′, E107° 40′, with 1200 m altitude above sea level. The soil is Helou soil and the parent material of the soil is deep mediumloam Malan Loess. The weather is warm temperate semi humid continental monsoon climate with an mean air temperature of 9.1°C and an annual mean rainfall of 584 mm, 60% of which is from July to September. Frost free season is 171 days, and the water table ranges from 50 to 80 maters.
Data collection
Daily solar radiation data came from ground measurements fixed in the experimental station. The software of MiLOS520 automatic weather station was installed in the farm land at the Changwu ecoexperimental station on Loess Plateau. The data was measured with the high-preciouse equaipment and collected in 2005-2013. Diurnal instantaneous solar irradiances flux density (W/m2), the stability of the diurnal cloud cover (daily variation in cloud cover), the actual measured total solar radiation are used in this study. Instantaneous solar irradiances flux density automatically was recorded once an hour from 0:00, the beginning of a day, to 24:00, the end of the day. The condition of the daily cloudy cover is observed.
Mathematical model
In this study, the Gaussian curve is used for simulating the dynamic changes of hourly instantaneous solar irradiances flux density (W/m2) over time (24 hours a day). General Gauss model is:
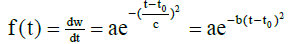 (2)
(2)
Here f (t) is instantaneous solar irradiances flux density (W/m2.s), t is time and t0 is the solar noon. the value of a is the peake of daily solar irradiances flux density when time t is equal to t0, and c is the steepness of the curve, the curve change rate of instantaneous solar irradiances flux density. The more the c is, the smaller the b is, and the smaller the steepness of the curve is because 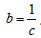
Because coefficient of determination reflects the weight of regression square sum in sum of squares of deviations and the more the coefficient of determination is, the higher the accuracy is, and the smaller root mean square error (RMSE) is, and the more the accuracy is. So we chose coefficient of determination R2 and root mean square error (RMSE) to express the fitting accuracy of Equation (2).
Results
Daily variation law of the solar irradiances flux density
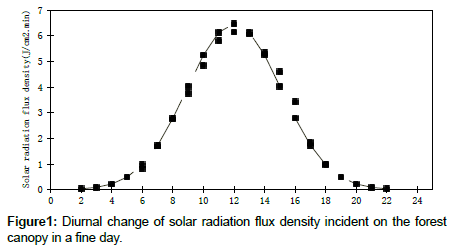
As the earth moves in its orbit, the total solar radiation flux density incident on the ground surface or the canopy of a forest takes on the daily change phenomenon, consisting of a symmetrical shape.
The amount of sunlight incident upon the Earth's surface at any point in space and time is a function of many variables. Those factors can be divided into two groups, one is based on the sky conditions, including the atmospheric and meteorological factors, while another is based on the geometric relationship between the fixed horizontal forest canopy or the ground surface and the sun. The factors are functions of time, t. When the sky conditions are constant, the solar radiation reaching a horizontal surface is the function of the geometric position between the fixed level plane and the sun, and solar radiation flux density is the only function of time, t [20-22]. The solar radiation flux increases nonlinearly with time t (0 ≤ t<t0). When time, t, is equal to time, t0, solar radiation flux reaches its peak. When time, t, exceeds time, t0, (24 ≥ t<t0), the solar radiation flux decreases nonlinearly with time, t (Figure 1).
The relationship between solar radiation flux density, 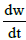 , and time, t, then be expressed as following
, and time, t, then be expressed as following
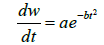 (3)
(3)
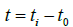
The value of main parameters a, b, t0, R2 and RMSE changed with time (date) and atmospheric and meteorological factors in Changwu Station is shown in Table 1 on 1-31, March 2013. The coefficient of determination, R2, is more than 0.87, and RMSE is quite smaller, showing that the Equation 3 can well describle the daily change of the solar radiation flux density in a day.
| Item | a | t0 | b | R2 | RMSE |
|---|---|---|---|---|---|
| 1 | 261.6 | 11.73 | 0.282008 | 0.9382 | 23.77 |
| 2 | 457.6 | 12.49 | 0.239234 | 0.8656 | 66.75 |
| 3 | 729.1 | 12.32 | 0.262605 | 0.9807 | 37 |
| 4 | 711.8 | 12.23 | 0.26001 | 0.9793 | 37.6 |
| 5 | 727.5 | 12.35 | 0.250438 | 0.9733 | 44.12 |
| 6 | 677.9 | 12.48 | 0.266454 | 0.9736 | 40.34 |
| 7 | 717.8 | 12.35 | 0.251762 | 0.9756 | 41.52 |
| 8 | 747.6 | 12.45 | 0.247402 | 0.9679 | 48.51 |
| 9 | 393 | 11.01 | 0.305344 | 0.9718 | 23 |
| 10 | 380 | 11.13 | 0.330797 | 0.9402 | 32.02 |
| 11 | 147.6 | 11.97 | 0.279877 | 0.8661 | 28.7 |
| 12 | 493.8 | 12.45 | 0.286287 | 0.9766 | 26.83 |
| 13 | 616.9 | 12.05 | 0.277085 | 0.9889 | 23.27 |
| 14 | 605.3 | 12.35 | 0.265111 | 0.9837 | 28.17 |
| 15 | 648.4 | 12.03 | 0.269324 | 0.9766 | 35.87 |
| 16 | 423.2 | 12.17 | 0.336474 | 0.9658 | 26.59 |
| 17 | 895.5 | 12.24 | 0.263019 | 0.9845 | 40.6 |
| 18 | 737.8 | 11.44 | 0.270416 | 0.9785 | 39.05 |
| 19 | 864.8 | 12.37 | 0.267594 | 0.9637 | 60.24 |
| 20 | 520.3 | 12.67 | 0.203459 | 0.8707 | 201.2 |
| 21 | 387 | 11.86 | 0.185117 | 0.8768 | 124.2 |
| 22 | 800.6 | 12.23 | 0.261575 | 0.9557 | 60.12 |
| 23 | 846.3 | 12.32 | 0.260417 | 0.9643 | 58.92 |
| 24 | 862.5 | 12.17 | 0.253743 | 0.9824 | 41.99 |
| 25 | 659.3 | 11.48 | 0.333333 | 0.9798 | 31.98 |
| 26 | 991 | 12.11 | 0.251004 | 0.9856 | 43.75 |
| 27 | 976.6 | 11.99 | 0.257003 | 0.984 | 45.21 |
| 28 | 923.6 | 12.04 | 0.252781 | 0.9759 | 52.81 |
| 29 | 684.8 | 12.3 | 0.228258 | 0.8839 | 92.41 |
| 30 | 928.5 | 12.1 | 0.254647 | 0.9848 | 41.82 |
| 31 | 659.5 | 11.46 | 0.281294 | 0.9503 | 52.85 |
Table 1: The change of main parameters with date in the diurnal change model of the instantaneous solar radiation incident on the horizontal surface in Changwu, China.
The Equation of the daily solar energy
Because the instantaneous solar flux density received on the horizontal surface is a successive function of time, t, throughout the day, Equation 3 is integrated over a 24-hour period from 0 to 24 hour in a day. The daily total solar energy therefore can be obtained by
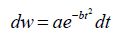
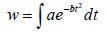
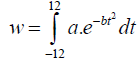 (4)
(4)
The Equation is evaluated from –12 to 12 to account for the 24 hours in a day with the average t0=12 because the value of t0 varies from 11. 00 a. m. to 14.00 p.m (Table 1) apart from some special day in which the sky condition change dramatically. The units of a and t in the right side of Equation are not unite, so a constant K is needed to unite the unit of a and t. When the unit of a is w/m2 or J/cm2. min, and the unit of time is hour, then unit transformation coefficient, K, is equal to 60, so Equation 3 can be rewritten as following:
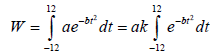 (5)
(5)
Let bt2 equal ξ2. When the time, t, tends to ± ∞, ξ tends to ± ∞ respectively. Then when time t is equal to 12 or -12, the value of solar radiation flux density, dw/dt, is so small that it can be neglected.
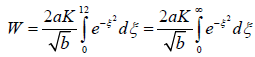 (6)
(6)
Generally, on calculating the daily solar energy, we consider the value of dw/dt to be zero because when time, t, is less than -12 or greater than 12, dw/dt is very smaler and approach to zero. So,
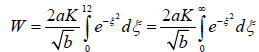 (7)
(7)
Let ξ2 equal x,
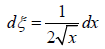
Because
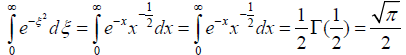 (8)
(8)
Inserting the Equation (8) into the Equation (7) yields
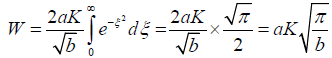 (9)
(9)
Here, W is the total solar energy incident on the horizontal surface or the canopy of a forest per square meter (J/m2), a and b are the same as Equation 3, π is the ratio of the circumference of a circle to its diameter, and K is the unit's conversion coefficient. When time, t, expressed in hour, K is 60.
If the value of solar radiation flux density, dw/dt at time t>12 or t<- 12 is so big that it can’t be neglected, then Equation 10 can be used to calculated daily solar energy with progression method:
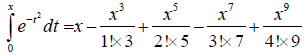 (10)
(10)
It can be seen from Table 1 that the smaller the change of weather conditions in a day is, the larger the value of R is. In a fixed investigated position at the three-time scales such as a year, a month, and a day, the smaller the time scale is, the more stable the sky conditions are, this is the reason why the diurnal solar radiation change with time, t, in most of days investigated in the growing seasons or a year can be described by Equation 3.
Discussion
When the solar radiation flux density passes through the earth’s atmosphere, the solar energy is dramatically reduced and dissipated in many ways. Part of the energy is reflected and part absorbed by the atmosphere, by clouds and other masses of solid particles in the atmosphere, then by the vegetation, and finally by the earth itself. The greater the amount of atmosphere through which the sun's radiation must pass is, the higher the percentage of the solar radiation flux density that absorbed or scattered and not received on the earth's surface is. As the solar energy is dissipated, the radiation wavelengths are changed. The shorter ultraviolet rays are almost completely absorbed by the atmosphere. The solar radiation with wavelengths ranging from approximately 0.4-0.7 μ (photosynthetic active radiation ) is visible to the unaided human eye and is termed light and accounts for approximately one-half of the total solar radiation flux density reaching the Earth’s surface. When the sun is low on the horizon, therefore, very little ultraviolet radiation reaches the land surface, and more infrared radiation reaches the earth than light. The solar radiation flux density reaching the horizontal surface is composed of three terms, direct radiation, scattered radiation, and infrared radiation or long-wave radiation. The direct radiation and scattered radiation only exist in the day, and the long-wave radiation exists 24 hours period of a day.
When author first study the change of solar radiation with time in a day, solar radiation data from the sunrise to the sunset were measured by ZD-√ʬ?¬°luxmeter, made in China, expressed in illuminance because the only measured light and recorded every two hours a day in Guyuan county in the Ningxia Hui Autononmous Region of China. Because coefficient of determination, R2, is a good index to reflect the degree a model to describle daily change of the total solar radiation. Although the cosine Equations can be used to describe this daily change of the total solar radiation flux density, but the normal distribution Equation has a higher coefficient of determination, R2, than that of the cosine Equation. In addition, because the cosine Equation can only express the solar radiation flux density from sunrise to sunset, so we decided to use the normal distribution Equation to describle the diurnal change of the total solar radiation flux density incident on the ground surface and found the daily change of the total solar radiation flux density well related with and explain the diurnal change of temperature, dumidity, the rate of plant photosynthesise, transpiration and evapotranspiration [22].
The luminometer has a higher response value to the solar radiation, it therefore cannot be used to measure the smaller solar radiation flux density throughout the day, especially solar radiation flux density during the periods from 0:00 to the sunrise and the sunset to 24:00 in a day. Total solar radiation flux density and illuminance are related; however, approximate conversions are possible [22] and Equation 3 can be used to describe solar radiation data from different places with different radiometer [20].
In order to prove this, the data of the diurnal change of the solar radiation flux density measured from 5 a.m. to 18 p.m., once every hour on 18, August 1983, a fine day in Changling (44°20′ N, 123° 50′E), Jilin province of China reported by Zu was used to prove the hypothesis. The result showed that the relationship between solar radiation flux density and time t can be described with Eq. 3 with an R value of -0.966966 (sample number, n=14). The solar radiation flux density was again measured from 6 a.m. to 18 p.m. once every hour on 11 July 1959, this time on a cloudy day. The daily total solar energy is 2249.7 (J/cm2) and on 12 July, 1959, a fine day, the daily total energy is 2892.4 (J/cm2) in Zijin mountain, Nanjing city of China (32°05'N,118°52'E) reported by Hong et al. and so on in different location in China, the expected results were obtained, and the values of R were -0.986369 on a cloudy day and -0.990669 on a fine day (n=13).
The amount of the instantaneous global solar radiation flux density incident on the horizontal surface, coming directly or indirectly from the sun, is composed of three parts, direct radiation, scattered radiation, and thermal radiation streaming downward from the atmospheric hemisphere. The former two terms exist in the daytime, but thermal radiation exists throughout a day, so the amount of the instantaneous global solar flux density always is bigger than zero in a 24-hour period. Generally, the sky conditions are stable throughout a day, the global solar radiation flux density received on the horizontal surface is only a function of time t of a day [20,22] and Equation 3 can be formally described.
There are three inflection points in the daily change model of solar radiation flux density, one is the solar radiation flux density when the time, t, equals the solar noon, t0, and the other two are the solar radiation flux densities at the two sides of the model. If we observed the solar radiation flux densities at the three inflection points of the daily solar radiation flux density, we can get the daily change model of the solar radiation flux density.
According to Hong et al.’s report, on a fine day, the relative error is 3.8%.
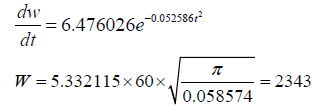
On a cloudy day, the relative error is 4.1%.
This showed that the Equation 3 can be used to better describe the daily change of the amount of the instantaneous global solar flux incident on the horizontal surface and the Equation 9 can be used to evalue the the daily solar energy. The Equation 9 is easy to use and has high accurate. If the Equation 9 ca not meet the error range, one can use Equation 4 and is integrated over a 24-hour period from 0 to 24 to evaluate the daily solar energy.
Conclusion
Generally, the sky conditions are stable throughout a day, the solar radiation is the function of time t, and the daily variation law of solar radiation, the relationship between solar radiation flux density and time, t can be described with Equation 3, which can almost complete explain the daily change of temperature, dumidity, the rate of plant photosynthesises, transpiration and evapotranspiration and the total solar energy per square centimeter is Equation 9.
In fact, the sky conditions vary with time, t, in a day because of atmospheric motion, and does not completely satisfy the stable sky conditions. For this reason, the value of R always approaches to 1.0, but it dos not equal 1.0. In a fixed level position or the canopy of a forest, the smaller the time scale from a year, to a month or to a day is, the more stable the sky conditions is, so daily solar radiation flux density change in most of the days in growing season or a year can be described by Equation 3 and the total solar energy per square centimeter can be estimated by Equation 9. There are three inflection points in the daily change model of solar radiation flux density. If we observed the solar radiation flux density at the three inflection points of the daily solar radiation flux density, we can get the daily change model of the solar radiation flux density.
Acknowledgements
The author thank Professor Horton for their helps to edit the paper, thank X. P. Zhang for her preparing Table 1. This study was supported by the National Science Fund of China (Project No. 41071193,41271539).
References
- Aman M (2015) A review of Safety, Health and Environmental (SHE) issues of solar energy system. Renewable Sustainable Energy Rev 41: 190-1204.
- El-Sebaii AA (2010) Global, direct and diffuse solar radiation on horizontal and tilted surfaces in Jeddah, Saudi Arabia. Appl Energy 87: 568-576
- Guo ZS, Zhang XP (2015) Diurnal change of the instantaneous solar radiation flux density to the horizontal surface, in the materials science and energy engineering. Chung, Li (eds). World Scientific Press, Singapore. pp. 608-616.
- Spurr SH, Barnes BV (1980) Forest Ecology. John Wiley & Sons, USA.
- Goss G (1986) Production maximalen de matière Sèche et rayonnement solaire interceptè par un couvert vegetal. Agoronomie 6: 47-56
- Arkebauer TJ (1994) In defense of radiation use efficiency: A response to demetriades. Agric Meteorol 68: 221-227
- Olesen JE, Grevsen K (1997) Effects of temperature and irradiance on vegetative growth of cauliflower (Brassica oleracea L. Botrytis) and broccoli (Brassica oleracea L. italica). J Exp Bot 313: 1591-1598.
- Linder S (1987) Responses to water and nutrients in coniferous ecosystems. Potentials and limitations of ecosystems analysis. Ecol Studies 61: 180-202.
- Cannell MJ (1989) Physiological basis of wood production: A review. Scand J For Res 4: 459-490.
- Albaugh (1998) Leaf area and above- and belowground growth responses of loblolly pine to nutrient and water additions. For Sci 2: 317-328
- Shukla KN, Rangnekar S, Sudhakar K (2015) Comparative study of isotropic and anisotropic sky models to estimate solar radiation incident on tilted surface: A case study for Bhopal, India. Energy Reports 1: 96-103
- Wu GF, Liu Y, Wang T (2007) Methods and strategy for modelling daily global solar radiation with measured meteorological data- A case study in Nanchang station, China. Energy Conversion Manag 48: 2447-2452.
- Buluta H, Büyükalaca O (2007) Simple model for the generation of daily global solar-radiation data in Turkey. Appl Energy 84: 477-491
- Janjai S, Pankaew P, Laksanaboonsong J (2009) A model for calculating hourly global solar radiation from satellite data in the tropics. Appl Energy 86: 1450-1457
- Lee R (1978) Forest microclimatology. Columbia University press, NY, USA.
- Gates (1980) Biophysical Ecology. Springer-Verlag, Heidelberg, Berlin, Germany.
- Zu YG (1982) Introduce of energy ecology. Jilin Science and Technology Publishing House. Changchun, China.
- Hong QF (1963) Microclimate of Masson Pine young Forest. Chin J Sci 283-288.
- Boznar MZ (2015) Radial frequency diagram (sunflower) for the analysis of diurnal cycle parameters: Solar energy application. Appl Energy 154: 592-602
- Guo ZS (1998) Research of the effects of Seabuchthorn shrubbery on its microclimate material of International Symposium on Sea buckthorn. Russia. pp. 96-98.
- Guo ZS (2014) Theory and practice on soil water carrying capacity for vegetation. Chinese Science Press, China.
- Guo ZS, Si L, Liu XD, Liu KJ (1991) A preliminary study on microclimate in little leaf pea shrub shrubbery. Memoir of NISWC Academia Sinica and Ministry of water Conservation 14: 84-95.
Relevant Topics
- Atmosphere
- Atmospheric Chemistry
- Atmospheric inversions
- Biosphere
- Chemical Oceanography
- Climate Modeling
- Crystallography
- Disaster Science
- Earth Science
- Ecology
- Environmental Degradation
- Gemology
- Geochemistry
- Geochronology
- Geomicrobiology
- Geomorphology
- Geosciences
- Geostatistics
- Glaciology
- Microplastic Pollution
- Mineralogy
- Soil Erosion and Land Degradation
Recommended Journals
Article Tools
Article Usage
- Total views: 9770
- [From(publication date):
September-2017 - Sep 02, 2025] - Breakdown by view type
- HTML page views : 8702
- PDF downloads : 1068