Research Article Open Access
Was Guinea the Source of the Ebola Virus contagion? Evidence via a Dynamic Equicorrelation Model
Nadhem Selmi*Department of Quantitative Methods, Faculty of Economics and Management, University of Sfax, Tunisia
- *Corresponding Author:
- Nadhem Selmi
Department of Quantitative Methods
Faculty of Economics and Management
University of Sfax, Tunisia
Tel: +216 74 242 951
E-mail: nadhem.selmi@yahoo.fr
Received date: October 30, 2015; Accepted date: January 04, 2016; Published date: January 14, 2016
Citation: Selmi N (2016) Was Guinea the Source of the Ebola Virus contagion? Evidence via a Dynamic Equicorrelation Model. J Emerg Infect Dis 1:106. doi:10.4172/2472-4998.1000106
Copyright: © 2016 Selmi N. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Journal of Infectious Disease and Pathology
Abstract
Forecasting the death number and co-movement case evolution is critically important in investigating the Ebola virus spreading phenomenon. To this end, it is crucial to examine investigate patterns and trends in correlations over time using daily figures data relevant to three major West African countries (Guinea, Liberia and Sierra lione) during the period ranging from March 3, 2014 to February 02, 2015. The aim is to show that several countries co-movements are possible to be simultaneously modeled by means of DCC, ADCC, GDCC, AGDCC and DECO models. Empirically, it has been discovered that correlations have significantly registered an upward trend for both countries Guinea and Sierra-Lione. Based on a time-varying measure of dynamic conditional correlation, it turns out to be impossible for a long-only virus transmission by itself to circumvent the increasing correlations, by means of adjusting the Ebola outbreak over time. However, some evidence has been attained highlighting that the DECO estimation model is actually possible, and proved that the number of Ebola-related deaths does indeed increase after three month lapse. JEL Classification: G12
Keywords
Ebola virus; Guinea; Dynamic conditional correlation (DCC); Dynamic equicorrelation (DECO)
Abbreviations
A-DCC: Asymmetric Dynamic Conditional Correlation; AG-DCC: Generalized Asymmetric Dynamic Conditional Correlation; BEKK: Baba, Engle, Kraft and Kroner; DECO: Dynamic Equi-Correlation Models; DCC: Dynamic Conditional Correlation; G-DCC: Generalized Dynamic Conditional Correlation; WHO: World Health Organization
Background
It is worth mentioning that the virus discovery dates back to 1976, when the first recorded outbreak took place in Zaire, now the Democratic Republic of Congo, in an area near the Ebola River, after which the decease dubbed. It then hit 318 people and killed 280. Its origin is debated up to this day. According to a common assumption, some species living in tropical forests of Central and West Africa would be the natural host of the Ebola virus. Other animals are also considered to participate in the transmission cycle. Five viral species have so far been identified, but the most important of which, thought to be responsible for the vast majority of contamination are: the Zaire strain-mutation which currently prevails, and Sudan one.
Noteworthy, the Ebola virus comes sporadically and at irregular intervals. The latest resurgence starts date of the year. The outbreak was first reported to occur in Guinea’s, forest before spreading to Liberia, Sierra-Leone and Nigeria. Until recently, the virus has been raging mainly in central and eastern Africa. From 1976 to 2012, and in addition to the Democratic Republic of Congo and Sudan, three other countries had been affected by serious epidemics namely: Gabon, Uganda and Congo. Together, they have recorded more than 2,200 people killed in forty years, much less than the Acquired Immune Deficiency Syndrome virus and malaria. The case fatality rate is itself for higher: it varies from 25% to 90%, depending on the strain. According to the world health organisation (WHO), it currently stands within an average rate of 54%.
Transmission of virus among humans is the epidemic major vector. Transmission occurs through contact with an infected person’s body fluids adds [1-20]. “Just as blood, secretions or feces come into contact with mucous membranes, or wound, for infection to spread to a new host”. The contamination occurs most often, among relatives or caregivers. However, the dead are also contagious, and physical contact with a dead body is still too dangerous. Hence, funeral rites play a crucially important role in transmitting the disease.
Currently, no treatment has been made available. In hospitals and treatment camps, caregivers simply undertake to help the body to fight the infection. “Unfortunately, we cannot do much to treat the disease and its symptoms”, in this case, it’s said that “Often, we simply moisturize injecting patients, and isolate them from the rest of the population to avoid contagion” [1]. Molecules and vaccines have already yielded some results on animals, but no results have been noticed on human beings. A serum called ZMapp, invented by the American company Mapp Biopharmaceutical, has been experimentally administered on two American patients. Worth noting in this regard, the United States has partially lifted restrictions on another experimental treatment achieved by the Canadian economy.
Concerned people and actors dedicated to deal with this particular problematic health crisis issue are likely to be concerned about this last resurgence of the virus. The WHO estimates that Ebola should continue to spread for several other months. As a matter of fact, Ebola has already witnessed a real spread all over the history of mankind, since its early discovery, and the number of victims is can hues to grow remarkably and exponentially it is also remarkably that noticed that its dispersion and multiplication among households has made the phenomenon even more complex and difficult to control master. Above all, several experts also worry that, for the first time, the disease has been discovered to thrive in urban areas. Worth-highlighting also, the health personnel nimons and tasks have been even further by the local population expressed mistrusted towards the Western caregivers.
The Ebola Virus has relabeled a climax and proven to be the most infectious 2014’s contagion since its appearance in 1976, through several studies do not know exactly how it has scored such noticeable spreads [2,3,5,6,10,15,16,19,21,22], they know that it can be transmitted by direct contact with infected blood, especially through contaminated needles, and, possibly are directed an infected person’s nasal or respiratory secretions. Health studies and family members to people who have the risk of virus infection. It is used to take blood samples to constitute a major biological cause, as extreme needle-stick injuries to healthcare workers can likely well transmit the infection to them. Moreover, some African countries who can contribute to transmit the Ebola virus. For instance, some funeral rites require a ritual cleaning of the body, which involve carrying holding and hogging the deceased firmly, which makes this blood or other body infected. Besides, monkey meat is considered as a delicacy in some parts of West Africa. In this respect, some studies recommend that people should not eat such meat as it can contain traces of the Ebola virus, which can well infect nonhuman primates like monkeys and chimpanzees [5,10,15,18,19,21].
The paper is structured as follows: Section 2 is devoted to provide a brief outline of dynamic conditional correlation (DCC), asymmetric dynamic conditional correlation (A-DCC), generalized dynamic conditional correlation (G-DCC), generalized asymmetric dynamic conditional correlation (AG-DCC) and dynamic equi-correlation (DECO) correlation models, with special emphasis being placed on large systems’ estimation. Section 3 is dedicated to highlight the relevant data, as well as empirical results which are with regard to time variation pertinent to international equity market correlations. As for section 4, a real-time forecasting exercise is conducted, while section 5 bears the conclusion and some perspective work lines.
Methods
DCC multivariate GARCH models
As a starting point, the return equation can be presented as:
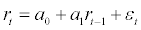 (2.1)
(2.1)
where 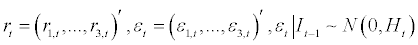
Then, we employ the multivariate conditional variance Ht:
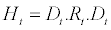 (2.2)
(2.2)
Where Dt is the (n × n) diagonal matrix of conditional standard deviations from univariate GARCH models with 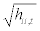 on the ith diagonal, (i =1,...,n) ; next the matrix of conditional correlation is:
on the ith diagonal, (i =1,...,n) ; next the matrix of conditional correlation is:
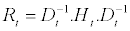 (2.3)
(2.3)
The DCC model developed by [7] includes a two-stage estimation of the conditional covariance matrix Ht. The primary one is a series of univariate GARCH estimated, where the univariate volatility models are fitted for each of the deaths and this way we obtain the estimations of 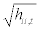 . The second stage is the correlation estimated where the number of deaths residuals is transformed by their estimated standard deviations from the first stage. That is,
. The second stage is the correlation estimated where the number of deaths residuals is transformed by their estimated standard deviations from the first stage. That is, 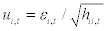 , where ui,t is used to estimate the parameters of the conditional correlation.
, where ui,t is used to estimate the parameters of the conditional correlation.
Furthermore, the evolution of the correlation in the DCC model is given by:
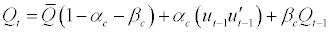 (2.4)
(2.4)
Where 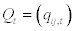 the n × n covariance matrix of ut is mean reverting as long as
the n × n covariance matrix of ut is mean reverting as long as 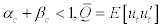 is the n × n unconditional variance matrix of ut. Otherwise, the correlation matrix Rt can be indicated as:
is the n × n unconditional variance matrix of ut. Otherwise, the correlation matrix Rt can be indicated as:
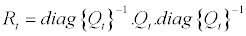 (2.5)
(2.5)
A typical element of Rt is presented as:
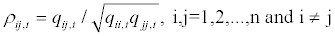 (2.6)
(2.6)
In a bivariate case the correlation coefficient can be expressed as:
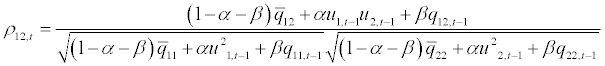 (2.7)
(2.7)
The DCC model used in this study includes two stages in the estimation process to maximize the log-likelihood function. Hence, this function can be written as the sum of one volatility part and one correlation part:
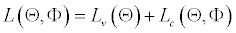 (2.8)
(2.8)
Then the log-likelihood function is presented as:
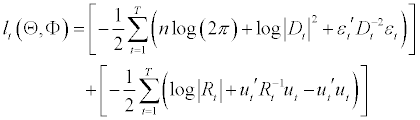 (2.9)
(2.9)
Asymmetric DCC Model (A-DCC)
A part from the DCC model, we also consider it useful to appeal to the A-DCC specification of [4]. The A-DCC model is often applied to introduce asymmetries revolve in the correlation dynamics. Such a choice is often applied made because the DCC pertaining correlations usually follow a scalar Baba, Engle, Kraft and Kroner (BEKK)-like process which wakes it too restrictive to apply the model on the entirely of series at once. In addition to the DCC, the A-DCC model is also subject of application. The A-DCC (1,1,1) model is expressed as:
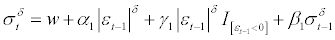 (2.10)
(2.10)
 (2.11)
(2.11)
Generalized DCC (G-DCC) model
A major strand of the DCC-related literature has proposed to introduce certain extensions in the DCC model with richer dynamic, see, for instance [12] as well as [2], among others. As for [4] who propose a BEKK-type generalization of the model, they have proposed following a second possible approach. In the G-DCC model version setup by [4], the following equation is applied to help drive the correlation dynamic:
 (2.12)
(2.12)
Where: A and B are n * n diagonal matrices1. Consequently, the individual elements dynamics of the matrix Qt turn out to be specified as follows:
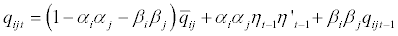 (2.13)
(2.13)
Even though this generalized model versions does help provide additional further flexibility to Engle’s specification, the number of parameters liable to estimation tends to increase considerably, though still feasible (it is linear worth regard to the correlations’ number, yet quadratic with respect to the number of deaths caused by the Ebola virus)2.
Multivariate M-GARCH-GDCC process
On a second stage, having obtained the conditional variances as derived from equation (2.5), we then proceed with studying the conditional correlations. Firstly, we undertake to illustrate the conditional covariance matrix such as:
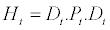 (2.14)
(2.14)
Where the diagonal matrix Dt denotes the conditional standard deviation as derived from equation (2.5). The standardized residuals matrix Zt is utilized to estimate the A-DCC process parameters as introduced by [4]. The AG-DCC process progression specified as follows:
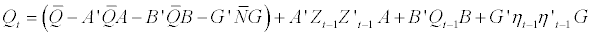 (2.15)
(2.15)
Where 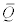 and
and 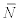 stand for the unconditional correlation matrices of Zt and
stand for the unconditional correlation matrices of Zt and 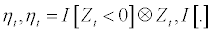 is a (k ×1) indicator function that takes value one if the argument is true and zero otherwise, while ⊗ indicates the Hadamard product), and
is a (k ×1) indicator function that takes value one if the argument is true and zero otherwise, while ⊗ indicates the Hadamard product), and 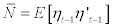 A-DCC(1,1) is recognized as a special case of the AG-DCC(1,1) process once matrices A, B, and G are replaced by the scalars (a1, b1 and g1). Cappiello L et al (2006), explain that Qt is definitely positive with a probability of one if
A-DCC(1,1) is recognized as a special case of the AG-DCC(1,1) process once matrices A, B, and G are replaced by the scalars (a1, b1 and g1). Cappiello L et al (2006), explain that Qt is definitely positive with a probability of one if 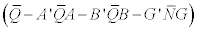 is positively defined. Then, the correlation matrix Pt be estimated as:
is positively defined. Then, the correlation matrix Pt be estimated as:
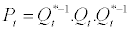 (2.16)
(2.16)
Where: 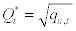 is a diagonal matrix through a square root of the ith diagonal components of Qt on its ith diagonal position.
is a diagonal matrix through a square root of the ith diagonal components of Qt on its ith diagonal position.
As for the standardized residuals and standardized negative residuals, along with the dynamics of Pt in the asymmetric DCC process of order (s,u) they are given by the following two equations:
 (2.17)
(2.17)
Where:  ,
,
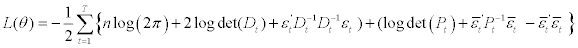 (2.18)
(2.18)
The Dynamic Equi-Correlation approach
Provide in [8], the DECO model can be regarded as a special case of the DCC model in which correlations prove to be equal across all country-pairs while the so-called equi-correlation turns out to be changing over time. The resultant dynamic correlation can be conceived to stand as an average dynamic correlation among the analysis concerned countries. Following [8], the dynamic rank equicorrelation matrix is parameterized in our context as being:
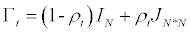 (2.19)
(2.19)
Where: IN denotes the n-dimensional identity matrix and JN*N is an N * N matrix of ones. The inverse and determinants of the rank equi-correlation matrix, Γt, are given by:
 (2.20)
(2.20)
The ease with which the correlation matrix is inverted helps ensure that the model can be estimated with large sets of assets using conventional maximum likelihood estimation. The dynamic equicorrelation parameter, ρt such a simple linear formats:
 (2.21)
(2.21)
Where: ut represents the equi-correlation update. With regard to our proper empirical application, the following correlation updating rule is applied:
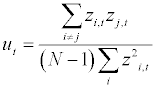 (2.22)
(2.22)
Although the DECO model may apparently been to be restrictive, it may well prove to result in superior correlation estimates once the true correlations are discovered to be too close to each other across assets. In such a case the DCC and BEKK model may well both provide noisy estimates of the correlation paths. Hence, the performance of the DECO in relation to the DCC, A-DCC, G-DCC and AG-DCC models is thus very much sample dependent.
Discussion
Data and descriptive statistics
The present paper applied data pertain to a too-case daily closing numbers of total cases and total deaths indexes. Data relative to Guinea, Liberia and Sierra Lione pertaining indexes are available from the Centers for Disease Control and Prevention. All data are denominated according to the number of people. A total of 202 observations have been collected over the period ranging from March 3, 2014 to February 02, 2015.
For an appropriate estimation of the conditional variance and the conditional correlation coefficient it’s implemented, that the sample descriptive statistics should be preliminarily analyzed. Table 1 below, displays the six serious sample cases (total cases and total deaths concerning the three countries3).
| Guinea | Liberia | Sierra Lione | ||||
|---|---|---|---|---|---|---|
| T cases | T deaths | T cases | T deaths | T cases | T deaths | |
| T | 102 | 102 | 102 | 102 | 102 | 102 |
| Mean | 770.8 | 486.617 | 2100.676 | 961.666 | 1966 | 558.66 |
| SD | 867.178 | 536.97 | 2973.55 | 1289.565 | 3039.49 | 839.48 |
| Skewness | 1.128* | 1.204* | 1.113* | 0.936* | 1.618* | 1.839* |
| kurtosis | 0.086 | 0.503 | -0.372 | -0.789 | 1.450* | 2.790* |
| J-B | 21.697* | 25.737* | 21.663* | 17.565* | 53.45* | 90.60* |
| ARCH | 0.648** | 0.538** | 0.825** | 0.756** | 0.689** | 0.579** |
Table 1: The descriptive statistics of the total cases and total deaths.
In this regard, the number of cases denotes that the figure turns out to be rather important with respect to Liberia (2100.676) than to Guinea and Sierra-Lione. Still with Liberia, the average number of deaths appears to be higher than that pertaining to the other countries in the sample. Meanwhile, the standard deviation reveals well that the total number of deaths in Guinea proves to denote the highest level of risk (Standard deviation=536.97). The number of total cases in Sierra Lione express the highest degree of incurred risk (Standard deviation=3039.49). The reason for such a high risk level could be resulted in the fact that this study period is discovered to be an extraordinary period with respect to all the studied indices. The Skewness coefficients indicate the asymmetric and left-skewed distribution pertinent to Guinea, Liberia and Sierra-Lione represents respective total cases and deaths. The excess 3 kurtosis coefficients exhibit a leptokurtic distribution concerning the Sierra-Lione total cases and deaths.
As for the Jarque-Bera (J-B) normal distribution test, it shows well that returns are in their entirety, not normally distributed. A further testing of the cases and deaths’ autocorrelation is also implemented through application of Ljung-Box statistic. This also implies that the heteroscedasticity of total cases and deaths should undergo certain temporal changes. Such a result suggests the use of autoregressive conditional heteroscedasticity (ARCH) model’s estimation and variance.
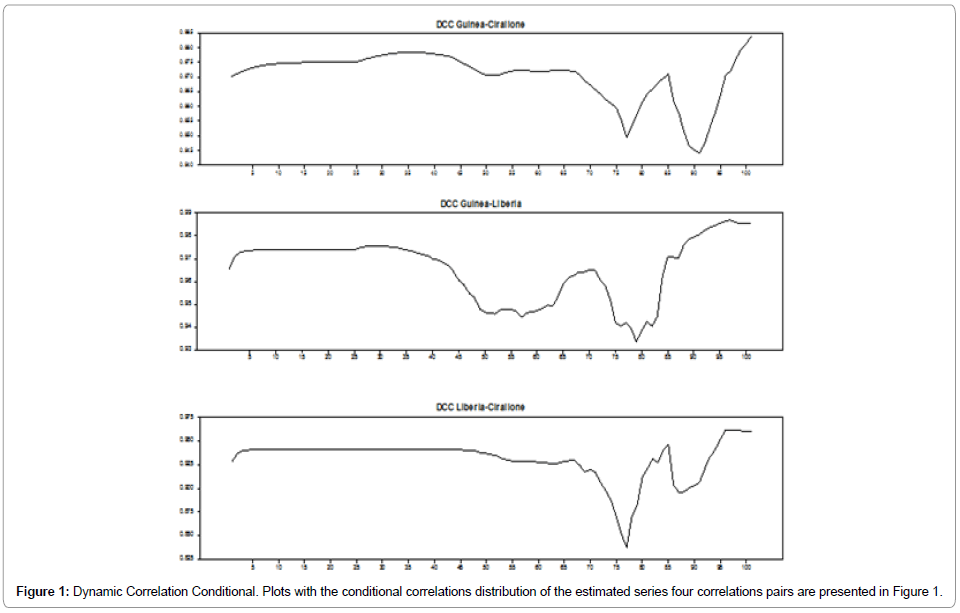
In a first reach and concerning the DCC model, we consider examining the studied countries relevance co-movements among number of deaths. In a second place, we undertake to analyze these countries’ respective co-movements between the number of deaths in total cases and total deaths. Table 2, below illustrates the DCC, A-DCC achieved results (N.B the conditional correlations equation; the mean and variance equations are depicted in the figure 1).
| Total Cases | Total Deaths | ||||||
|---|---|---|---|---|---|---|---|
| Guinea-Liberia | Guinea-Ciralione | Liberia- Ciralione | Guinea-Liberia | Guinea-Ciralione | Liberia- Ciralione | ||
| DCC | αc | 0.08 | 0.1 | 0.15 | 0.08 | 0 | 0.050* |
| βc | 0.75 | 0.52 | 0.42 | 0.75 | 0.691* | 0.94* | |
| A-DCC | θ1 | 0.312 | 0.774 | 0.612 | 0.827 | 0.691 | 0.543 |
| 0 | 0 | 0 | 0 | 0 | 0 | ||
| Φ1 | 0.93 | 0.485 | 0.199 | 0.445 | 0.612 | 0.746 | |
| 0 | 0.23 | 0.87 | 0.23 | 0 | 0 | ||
| τ1 | 1.44 | -2.6.10-6 | -1.8.10-4 | 0.286 | 0.428 | 0.249 | |
| 0 | 0.99 | 0.82 | 0 | 0 | 0 | ||
| BIC | 4919 | 4742.61 | 4994.44 | 4745.6 | 4548.809 | 4729.66 | |
| G-DCC | αi | 0.325* | 0.742* | 0.152* | 0.794* | 0.714 | 0.350* |
| 0 | |||||||
| αj | 0.306* | 0.793* | 0.462* | 0.869* | 0.788 | 0.525* | |
| 0 | |||||||
| βi | 0.946* | 0.538*** | 0.846* | 0.582* | 0.641* | 0.933* | |
| βj | 0.952* | 0.508*** | 0.767* | 0.382 | 0.484* | 0.826* | |
| BIC | 4903.12 | 4746.45 | 4956.21 | 4747.77 | 4543.86 | 4635.39 | |
| AG-DCC | α1 | 0.325* | 0.742* | 0.152* | 0.696* | 0.591* | 0.437* |
Table 2: Parameter Estimates for DCC, A-DCC, G-DCC, AG-DCC and DECO Models. Total cases and total deaths.
Regarding the A-DCC model, it has been shown that τ1 tends to zero for both countries pairs Guinea-Sierra Lione and Liberia-Sierra Lione in total panel boxes. Concerning the reimaging case, it has proved that conditional correlation is significant and positive, highlighting shock asymmetry through dynamic conditional correlations.
Regarding the G-DCC model, it has been the prevalence of increased shocks persistence throughout the entire cases caused by Ebola virus αi > αj with regard the two cases of Guinea-Liberia and Guinea-Sierra Lione, and inversely for pair case of Liberia-Sierra Lione αi < αj. α . This reveals well that Guinea turns out to be the native land of origin of the Ebola virus in all the affected cases. Regarding the total deaths cases, it has been revealed that based on the G-DCC model, αi < αj for all the studied cases indicating persistence of shocks and therefore, the highest likelihood of contagion. On proceeding to study contagion through the parameters βi, it has been proved that βi and βj appear to be significant and positive with respect to all study cases except for Liberia concerning the cases with βi>βj. This underlines the fact that βi.βj is positive with regard to all cases, indicating the propagation of shocks from Guinea to Liberia and Sierra Lione and from Liberia to Sierra Lione.
In addition to this, we go on with applying the AG-DCC methodology with the aim of testing correlation among the three selected counties. On the one hand, the outcome reveals the relationship binding the figures pertaining to some West African countries. On the other hand, the selected time periods help us well obtain the desired results. Table 2 also illustrates the asymmetric conditional correlation.
The second step consists in estimating the AG-DCC process while Table 2 bears the empirical result relevant to the entire sample period. Estimation at the standardized residuals parameter level (ai) and innovation at the level of the conditional correlation matrix dynamics (bi) are both discovered to be statistically significant at 1% threshold level, whereas the asymmetric term (gi) parameter appears to be statistically significant at 5% threshold level. Thus, the deal figures conditional correlation seems to be clearly far significantly influenced by negative innovations rather than by positive ones. As highlighted by Table 2, the empirical results are identified by a studied period. With reference to the asymmetric term 1 g parameter, concerning the entire period, it does not prove to be statistically significant within conventional levels, but it demonstrates the statistical significance at 1% level with respect to all cases, except for Guinea-Sierra Lione and Liberia-Sierra Lione compared to the entirety cases. It is also demonstrates that such results also prevail that the interdependence relationship between the numbers of deaths has evolved remarkably since the Ebola epidemic came into effect.
Besides, Table 2 also reports the Log-likelihood values corresponding to each of the four models. The DCC and A-DCC models dynamic correlations seem to be approximately the same for the GARCH model, while the AG-DCC model indicates different dynamics, with greater amplitude being reported in comparison with DCC, A-DCC and GD-DCC, which seem to follow a similar pattern. In effect, both GD-DCC and AGD-DCC indicate a similar pattern when using the GARCH specification. What should be noted is, all that models in their entity show a significant correlation among total cases and total deaths regarding the countries subject to this study. The maximum reached correlation was registered in August, showed that the AGD-DCC framework has proved to be more sensitive to incorporate negative news than have, the other processes.
The behavior is stabilized wisely respectively to the ADCC case with less than unity constraints on the parameters (equation 21). Yet, this has not been the case with DECO, as the constraint is placed sited on the equi-correlation parameter itself. The greatest similarity noticed between the A-DCC and the sample correlations is also reasonable when recalling that the sample correlation is but the MLE of the correlation assuming multivariate normality, and that the likelihood function employed in the A-DCC estimation is based on the Gaussian distribution.
The first, thing to observe is that the correlation distribution across models seems to be very variable. Across the four pairs, the DCC model highlights an extreme correlation level (0.97) for the Guinea- Sierra Lione pair, registered on April, 24. The lowest value registered for this pair is recorded to occur on December 11, with a value of 0.9. Besides, a strong dynamic correlation has been noticed to take place between Guinea and Sierra Lione (greater than 0.9), has indicated the existence of remarkable contagious transmission among both countries regarding the number of Ebola virus incurred deaths.
Concerning the couple Guinea-Liberia pair, it has been noticed that the dynamic correlation is discovered to be lower in respect to the previously treated couple. This indicates that the probability of contagion within this couple of countries is very low.
Regarding the third pair Liberia-Sierra Lione, one might well notice that the dynamic correlation proves to be significant (at 0.92) with a significant shock occurring on September 26. This finding highlights the spread of Ebola virus from Liberia to Sierra-Lione.
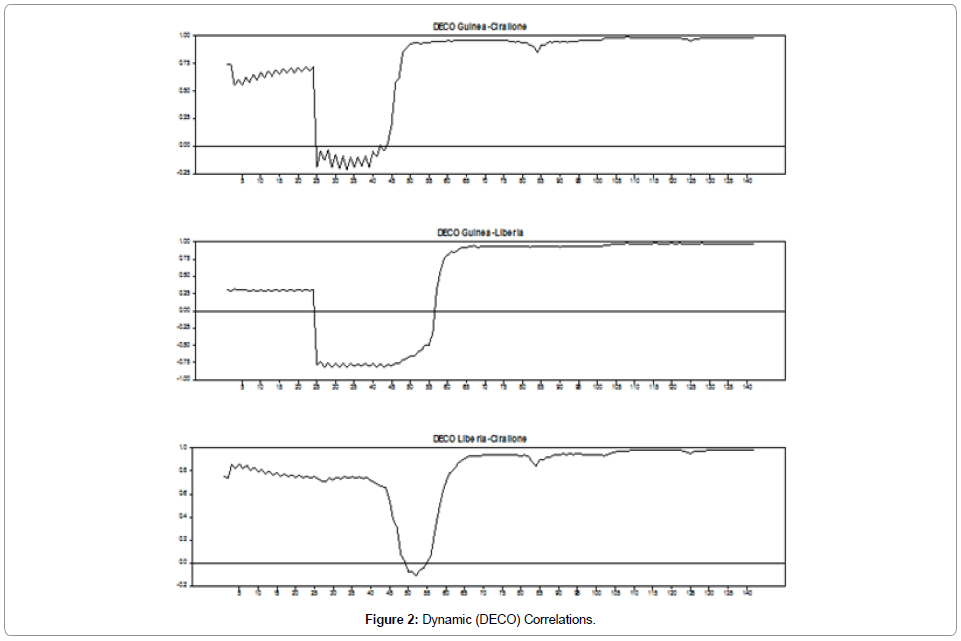
At this level, too-sample-period dynamic equi-correlations DECOs are reported. The left-side panels report the period ranging from March 01, 2014 to February 04, 2015, while the right-side panel’s report the period ranging between February 04, 2015 and August 18, 2015. As for the top panels, they report on developed markets, while the middle panel’s report African countries and the bottom panels reported on samples made up of developing the such as the African countries.
The parameters highest a value for Liberia relative to its value for Guinea testifies in turn the fact that volatility dynamics prove to be more persistent for Guinea. Furthermore, our attained results confirm also the asymmetry in volatility reaction toward the shock size. Indeed, the estimated value for γ1 is positive for both countries but sounds even higher for the Liberia case, suggesting that volatility dependency to market events is discovered to be even more important with respect to numbers of deaths.
The difference between the dynamic correlations figures respectively to both the DCC and the DECO processes is shown exactly in: the dynamic conditional correlations’ DECO falling spot prior to the DCC respective. In addition, shocks’ persistence turns out to be higher with respect to the DECO case than the DCC framework-a fact which has its explanation in the shock asymmetrical-phenomenon. The highest value attributed to this parameter through DECO as compared to its DCC model respective value, highlights the fact that volatility dynamics are more persistent with regard to DECO models. Moreover, our findings do also confirm the persistence of the asymmetry in the DCC response to the shock size. Indeed, the dynamic conditional correlation estimated value seems positive for both countries although it’s higher with regard to the DCC undertaking, suggesting that volatility dependence to market events proves to be more important with respect to the DCC.
Our forecast foreshadows that the dynamic conditional correlations show that it should be significant tending to 1 in its turn proves to show that the underlining contagion has been the source origin of the Ebola virus and its incurred death figures. Indeed, ever since February 2014, the Ebola epidemic has been the source responsible for over 1200 deaths in West Africa. Actually, Ebola is a highly contagious disease that has killed up to 90% of infected people, to which no widely-available, definite cure has so far been cured.
It is a “stylized fact” that correlations tend to increase under countries conditions [1]. A striking illustration may lie in Figure 2 which includes three coordinated sell-off events: March 3, 2014 to February 02, 2015 (flight-to-safety, observation 110), September 2014 (310) and January 2015 (145). For instance, in May 2014 a sharp drop in the index has been matched by a sharp rise in the equi-correlation. Around observation 260, there prevails a sharp drop in equi-correlation. This is mainly due to the drop witnessed in May 2014 which falls out within the 30-day window. The drop around December, 2014 results in a comparatively small increase in the number of equi-correlation though sizeable in relative terms. The August, 2014 sell-off has resulted in a noticeable equi-correlation rise. As for February, the effect left the by 150 day window around 320 has been difficult to detect.
Conclusion
Using the DCC, ADCC, GDCC, AGDCC and DECO models, we estimate the cross-correlation and volatility among the Guinea, Liberia and Sierra-Lione number of deaths and total cases from March 3, 2014 to February 02, 2015. Both time-varying correlations and realized distributions are explored. The results indicate that the distributions of intraday variances are skewed to the right and are leptokurtic. Furthermore, the Liberian numbers of deaths influence Guinea, but not vice versa. Hence, the DCC probability distribution of Guinea and Liberia displays high volatility accompanied with a high DCC value because of Guinea’s dominance. In the meantime, Sierra Lione has a spillover effect on London’s variance, and Liberia also has a co-movement effect on Guinea’s variance. The results of the DCC probability distributions thus show an overlap without dominance. Last, Guinea has a spillover effect on Liberia’s variance, while Liberia does not have any impact on New York’s variance. As such, the DCC probability distribution between Guinea and Liberia has a highly volatility with a high DCC value, and the high-DCC distribution is wider than the low-DCC distribution.
Conflict of interest
The author has no conflict of interest.
1The most generalized model representation should include full parameter matrices, but this will raise the well known course of dimensionality. DCC is a special version case of ADCC when τ1 = 0. The most generalized model representation should include full parameter matrices, but this will raise the well known course of dimensionality.
2The Asymmetric Generalized DCC in [4] includes an additional component accounting for the past negative shocks asymmetric impact on the correlation process.
3Guinea, Liberia and Sierra-Lione.
References
- Bégué G (2014) infirmière courage dansl’enferd’Ebola.
- Billio M, Caporin M (2009) A generalized dynamic conditional correlation model for portfolio risk evaluation. Mathematics and Computers in Simulation 19: 2566-2578.
- Borchert M, Mutyaba I, Van Kerkhove MD, Lutwama J, Luwaga H, et al. (2011) Ebola haemorrhagic fever outbreak in Masindi District, Uganda: outbreak description and lessons learned. BMC Infect Dis 11: 357.
- Cappiello L, Engle RF, Sheppard K (2006) Asymmetric Dynamics in the Correlations of Global Equity and Bond Returns. Journal of Financial Econometrics 4: 537-572.
- Chowell G, Hengartner NW, Castillo-Chavez C, Fenimore PW, Hyman JM (2004) The basic reproductive number of Ebola and the effects of public health measures: the cases of Congo and Uganda. J TheorBiol 229: 119-126.
- Dowell SF, Mukunu R, Ksiazek TG, Khan AS, Rollin PE, et al. (1999) Trans-mission of Ebola hemorrhagic fever: a study of risk factors in family members, kikwit, democratic republic of the congo 1995. J Infectious Dis 179: S87-S91.
- Engle R (2002) Dynamic Conditional Correlation: A Simple Class of Multivariate Generalized Autoregressive Conditional Heteroskedasticity Models. Journal of Business and Economic Statistics 20: 339-350.
- Engle R, Kelly B (2012) Dynamic Equicorrelation. Journal of Business & Economic Statistics 30: 212-228.
- Engle R, Kroner K (1995) Multivariate Simultaneous Generalized ARCH. Econometric Theory 11: 122-150.
- Ferrari MJ, Bjørnstad ON, Dobson AP (2005) Estimation and inference of R0 of an infectious pathogen by a removal method. Math Biosci 198: 14-26.
- Hafner CM, Franses HP (2003) A Generalized DCC model for Many Asset Returns. Econometric Institute Report EI 2003-18.
- Hervé R (2014) Vigie Ebola, un vaccinexpérimental sera testédèsseptembre. Sciences Avenir.
- Isaacson M, Ruppol JF, Collas R, Matundu N, TshibambaOmombo K (1976) Containment and surveillance of a hospital outbreak of Ebola virus disease in Kinshasa, Zaire.
- Legrand J, Grais RF, Boelle PY, Valleron AJ, Flahault A (2007) Understanding the dynamics of Ebola epidemics. Epidemiol Infect 135: 610-621.
- Lekone PE, Finkenstädt BF (2006) Statistical inference in a stochastic epidemic SEIR model with control intervention: Ebola as a case study. Biometrics 62: 1170-1177.
- Ndanguza D, Tchuenche J, Haario H (2013) Statistical data analysis of the 1995 Ebola outbreak in the democratic republic of Congo. AfrikaMatematika 24: 55-68.
- McKinley T, Cook AR, Deardon R (2009) Inference in epidemic models without likelihoods. Int J Biostat 5: 1557-4679.
- Raoul H (2014) Vigie Ebola. Un vaccinexpérimental sera testédèsseptembre. sciences Avenir.
- (1978) Ebola haemorrhagic fever in Zaire, 1976. Bull World Health Organ 56: 271-293.
- Sureau P, Piot P, Breman G, Ruppol F, Masamba M, et al. (1976) Containment and surveillanceof an epidemic of Ebola virus infection in Yambuku area, Zaire.
- White LF, Pagano M (2008) A likelihood-based method for real-time estimation of the serial interval and reproductive number of an epidemic. Stat Med 27: 2999-3016.
- WHO (2014) Disease Outbreak News.
Relevant Topics
Recommended Journals
Article Tools
Article Usage
- Total views: 11030
- [From(publication date):
March-2016 - Aug 25, 2025] - Breakdown by view type
- HTML page views : 10086
- PDF downloads : 944