Make the best use of Scientific Research and information from our 700+ peer reviewed, Open Access Journals that operates with the help of 50,000+ Editorial Board Members and esteemed reviewers and 1000+ Scientific associations in Medical, Clinical, Pharmaceutical, Engineering, Technology and Management Fields.
Meet Inspiring Speakers and Experts at our 3000+ Global Conferenceseries Events with over 600+ Conferences, 1200+ Symposiums and 1200+ Workshops on Medical, Pharma, Engineering, Science, Technology and Business
Editorial Open Access
Estimate the Population Density of Gold Nanoparticles in Suspensions from Experimental Data
| Lei Yu* | |
| Department of Chemistry and Biochemistry, Rowan University, Glassboro, New Jersey, 08028, USA | |
| *Corresponding Author : | Lei Yu Department of Chemistry and Biochemistry Rowan University, Glassboro, New Jersey, 08028, USA E-mail: Yu@rowan.edu |
| Received October 25, 2012; Accepted October 27, 2012; Published October 29, 2012 | |
| Citation: Yu L (2012) Estimate the Population Density of Gold Nanoparticles in Suspensions from Experimental Data. Biochem Physiol 1:e111. doi:10.4172/2168-9652.1000e111 | |
| Copyright: © 2012 Yu L. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. | |
Visit for more related articles at Biochemistry & Physiology: Open Access
| Gold Nanoparticles (AuNP) have been found many applications in chemistry and biochemistry, for example, as labels for bioanalysis or as payload carriers for biotherapeutics. Recently, investigations of the potential risks of the applications of AuNP and its products to human health and to the environment are also dynamic. It is very critical to know the mass or the number of nanoparticles in a sample in order to understand these biological and environmental effects. This requires analytical methods that focus on the average size of the particles, number of particles, and the total mass of particles in a liquid or solid sample. |
| Gold content in solutions can be measured by methods such as electrochemical methods, Inductively Coupled Plasma- Mass Spectrometry (ICP-MS), and Flame Atomic Absorption Spectrophotometry (FAAS). These methods measure the amount of total gold element in a solution after the chemical digestion of gold, usually by aqua regia or HBr/Br2 solutions. In 2008, National Institute of Standards and Technology (NIST) released AuNP standards with known gold concentration and average particles diameter of 10, 30, and 60 nm [1]. The gold content was measured by using inductivelycoupled plasma optical emission spectrometry (ICP-OES) after digestion. On the other hand, the average diameter of the AuNP was measured by Atomic Force Microscopy (AFM), Scanning Electron Microscopy (SEM), Transmission Electron Microscopy (TEM), Differential Mobility Analysis, Dynamic Light Scattering, and Small- Angle X-ray Scattering. In several recent reports the average diameter, total gold content, and number of AuNP have been characterized in natural water systems and uptake in cell lines. In these reports, a combination of TEM and ICP-MS, ICP-OES, or atomic absorption Spectrophotometry (AAS) was used for the AuNP characterization and determination. |
| Given the diameter of the AuNP and the total amount (in mole, mol/L, number of gold atoms, or gram) of gold, it seems not very hard to calculate the number of AuNP in a suspension: |
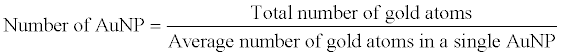 |
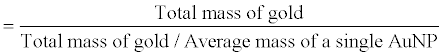 |
| Absolute monodisperse AuNP suspension does not exist. The diameter of the AuNPs in a synthesized suspension varies and usually follows a discrete log-normal distribution. Therefore, the diameter of the AuNP that has been used for the calculations refers to the mean value of the AuNPs in a suspension. The mean value is usually obtained by measuring the diameters of tens or hundreds AuNPs in their TEM image. The mean diameter was calculated by the individual diameters of measured AuNPs. Considering that there are many different statistical ways to calculate the mean value of a set of data, an accurate statistical mean should be used to calculate the number of AuNPs in a suspension and a nominal value that can be used to describe the size of AuNPs. |
| In this statistical discussion, AuNP population refers to the number of all the particles. Population equals to N means there are |
| N nanoparticle in a suspension. Given a suspension of AuNP has population of N; each individual AuNP can be identified as Pi, where i = 1 ~ N. Assume all the AuNPs are geometrically spherical. Particle Pi has a radii of ri. |
The arithmetic average, or the numerical average, radius of the
AuNPs, 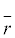 should be: should be: |
 (1) (1) |
| In this case, all the AuNPs have the same weight contributed to the average. The weight is assigned to be unity. |
| When the weight of AuNP Pi equals to the radius (ri) of the AuNP, the weighted average can be called radius average, which can be calculated as: |
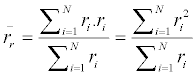 (2) (2) |
| When the weight of AuNP Pi equals to the cross-section area (πri2 ) of the AuNP, the weighted average can be called cross-section-area (CSA) average, which can be calculated as: |
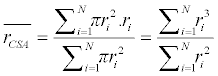 (3) (3) |
| When the weight of AuNP Pi equals to the surface area ( 4πr2i ) of the AuNP, the weighted average can be called surface-area (SA) average, which can be calculated as: |
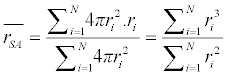 (4) (4) |
| When the weight of NP Pi equals to the volume ( 4 /3 ├ó┬?┬óπr3i ) of the NP, the weighted average can be called volume (V) average, which can be calculated as: |
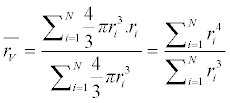 (5) (5) |
| For example, we have a set of 21 AuNPs. Each of these AuNP has different radius. We assuming r1 = 4.00 nm, while ri+1 ├ó┬?┬? ri = 0.10 nm. Then r21 is 6.00 nm. Following the above equations, the arithmetic and weighted average radius are calculated and summarized in table 1. |
| Weighted mean radii of AuNP should be obtained and used depending on the measurement methods. In these methods, the probabilities of each particle are picked and measured are identical or different. The probability may proportional to the radius, crosssection area, surface area, or volume, which are the weights of the mean. Currently, TEM is the prevailing method of AuNP radius measurement. When TEM is used, the probability of each AuNP is picked and measured is the same either by software or by operator. Therefore, the arithmetic mean values should be obtained by a number average of the measured radii of all AuNPs. However, depend on how these measured radii of AuNPs are used, statistical moment means should be considered when calculating the mean value. The moment mean radius of AuNPs can be calculated by equation: |
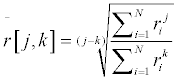 (6) (6) |
Therefore, the arithmetic mean, 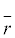 , corresponds to , corresponds to 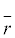 [1,0]; while
the weighted means, [1,0]; while
the weighted means, 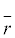 V V 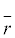 SA SA 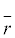 CSA , and CSA , and 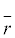 r correspond to r correspond to 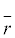 [4,3], [4,3], 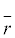 [3,2],
and [3,2],
and 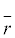 [2,1], respectively. With the concept of moment mean, the
number of AuNPs can be calculated more accurately. In experiments,
the total amount (mass or volume) of gold can be measured by ICPMS,
ICP-OES, electrochemistry, or AAS. The mean radius of AuNPs
can be measured by TEM. The number of the AuNP can be calculated
by dividing the total volume by the mean volume. For a spherical
particle, the volume equals 4/3
Πr3 . Here, the radius r should not be the
arithmetic mean of the radii measured by TEM; rather, it should be
the number-volumetric mean of the measured radii. In the context of
moment mean, the number-volumetric mean is [2,1], respectively. With the concept of moment mean, the
number of AuNPs can be calculated more accurately. In experiments,
the total amount (mass or volume) of gold can be measured by ICPMS,
ICP-OES, electrochemistry, or AAS. The mean radius of AuNPs
can be measured by TEM. The number of the AuNP can be calculated
by dividing the total volume by the mean volume. For a spherical
particle, the volume equals 4/3
Πr3 . Here, the radius r should not be the
arithmetic mean of the radii measured by TEM; rather, it should be
the number-volumetric mean of the measured radii. In the context of
moment mean, the number-volumetric mean is 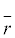 [3,0]: [3,0]: |
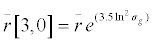 (7) (7) |
Therefore, the mean volume of AuNPs should be calculated by the
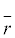 [3,0] value of all the measured AuNP radii, instead of the arithmetic
mean of the measured radii. [3,0] value of all the measured AuNP radii, instead of the arithmetic
mean of the measured radii. |
| The size distribution of synthesized AuNPs in dispersions is usually a log-normal distribution that produces a ├ó┬?┬?skewed├ó┬?┬Ł distribution curve.A geometric standard deviation (sg) should be calculated and provided. Then the number-volume mean radius can be calculated by the Hatch- Choate equation [2]. |
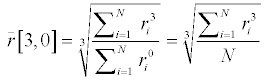 (8) (8) |
| In summary, in this essay, different ways to calculate the mean radii of AuNPs from experimental data are discussed. The calculations are based on statistical concepts of arithmetic mean, weighted means, and moment means. Previously, the mean values and the distributions of particles├ó┬?┬? size have been discussed intensively in statistics and engineering. As the application of AuNP becomes more and more popular, the characterization of the mean size of AuNP and the number of AuNP in the areas of chemistry, biochemistry, physiology, environmental science, and food science will be more and more frequent. We believe these different ways of calculation should be noticed when experimental data are processed. |
References |
Tables and Figures at a glance
| Table 1 |
Post your comment
Relevant Topics
- Analytical Biochemistry
- Applied Biochemistry
- Carbohydrate Biochemistry
- Cellular Biochemistry
- Clinical_Biochemistry
- Comparative Biochemistry
- Environmental Biochemistry
- Forensic Biochemistry
- Lipid Biochemistry
- Medical_Biochemistry
- Metabolomics
- Nutritional Biochemistry
- Pesticide Biochemistry
- Process Biochemistry
- Protein_Biochemistry
- Single-Cell Biochemistry
- Soil_Biochemistry
Recommended Journals
- Biosensor Journals
- Cellular Biology Journal
- Journal of Biochemistry and Microbial Toxicology
- Journal of Biochemistry and Cell Biology
- Journal of Biological and Medical Sciences
- Journal of Cell Biology & Immunology
- Journal of Cellular and Molecular Pharmacology
- Journal of Chemical Biology & Therapeutics
- Journal of Phytochemicistry And Biochemistry
Article Tools
Article Usage
- Total views: 13557
- [From(publication date):
December-2012 - Aug 18, 2025] - Breakdown by view type
- HTML page views : 8996
- PDF downloads : 4561
