Make the best use of Scientific Research and information from our 700+ peer reviewed, Open Access Journals that operates with the help of 50,000+ Editorial Board Members and esteemed reviewers and 1000+ Scientific associations in Medical, Clinical, Pharmaceutical, Engineering, Technology and Management Fields.
Meet Inspiring Speakers and Experts at our 3000+ Global Conferenceseries Events with over 600+ Conferences, 1200+ Symposiums and 1200+ Workshops on Medical, Pharma, Engineering, Science, Technology and Business
Research Article Open Access
Fast Side-Chain Dynamics: Measurement, Analysis, and Their Role in Protein Function
| Chad M Petit* | |
| Department of Biochemistry and Molecular Genetics, University of Alabama, USA | |
| *Corresponding Author : | Chad M Petit Department of Biochemistry and Molecular Genetics University of Alabama, 720, 20thStreet South Kaul Human Genetics, Room 452, Birmingham, AL 35294, USA E-mail: cpetit@uab.edu |
| Received February 06, 2013; Accepted May 13, 2013; Published May 16, 2013 | |
| Citation: Petit CM (2013) Fast Side-Chain Dynamics: Measurement, Analysis, and Their Role in Protein Function. Biochem Physiol S2:006. doi:10.4172/2168-9652.S2-006 | |
| Copyright: © 2013 Petit CM. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. | |
Visit for more related articles at Biochemistry & Physiology: Open Access
Abstract
Proteins are dynamic molecules that use coordinated atomic fluctuations to achieve proper function. These motions have fundamental implications for not only understanding how proteins function, but current methods of structure based drug design. In this review, we focus on providing an overview of the NMR experiments to detect side-chain motions and their applications, to characterize to conformational entropy, allostery, and proper protein function.
| Keywords |
| Entropy; Proteins; CAP; NMR |
| Introduction |
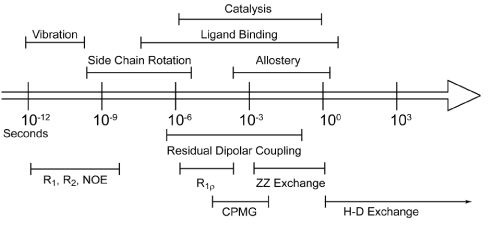
| Proteins in solution are not static entities, but are “kicking and screaming stochastic molecules” that depend on the coordination of atomic motions to function properly [1]. These motions occur over a large range of timescales [2,3], from bond vibrations on the picosecond time scale to the folding and unfolding of biomolecules that may take seconds or longer (Figure 1). While there have been many techniques developed to explore how these motions affect and sustain biological processes, NMR is a powerful technique that offers many advantages over others. Perhaps, the biggest advantage NMR offers is that it allows experimental examination of protein motions over a wide range of time scales, with atomic resolution. NMR has shown that biological processes such as conformational switching and catalysis are dependent on motions occurring on the microsecond to millisecond (μs-ms), often called “slow”, timescale [4-6]. However, not all proteins undergo significant motions on the slow timescale. In contrast, motions on the picosecond to nanosecond (ps-ns), often called “fast”, timescale occur in all proteins, many of which result from fluctuations of backbone and side-chain dihedral angles. This review focuses on how side-chain motions of methyl bearing residues are characterized using NMR, and what affect do these motions have on protein function. |
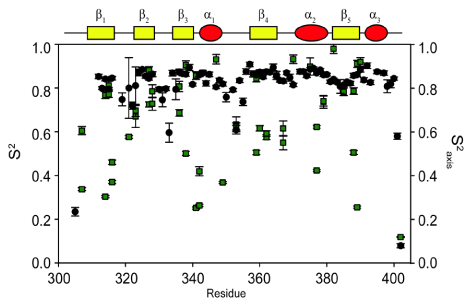
| The generalized order parameter, S2, is a rigidity parameter that represents the internal re-orientational freedom of a given bond vector on the ps-ns timescale [7,8]. S2 ranges from 0, corresponding to no favored position of the bond vector in the molecular frame, to 1 which corresponds to complete rigidity of the bond vector. For protein dynamics, order parameters are typically measured for a given bond vector, using NMR spin relaxation experiments. The most common bond vector motions measured are for backbone amide and side-chain methyl groups. As backbone amide order parameters provide information on site specific motions involving the main chain of the protein, the distribution of amplitudes of motion is relatively narrow throughout the protein for well folded and compact proteins. Conversely, side-chain order parameters, whose amplitudes are largely independent of secondary structure, vary considerably throughout the protein (Figure 2). What influences side-chain mobility is largely uncertain, as the amplitude of side-chain motions appear not to be correlated with packing density, depth of burial, or solvent accessible surface area [9]. However, a recent study by Fu et al. [10] uses high pressure NMR, to offer the intriguing idea that amplitudes of side-chain motions may be dictated by variations in the internal compressibilities of proteins. It is clear is that this variability facilitates modulation of protein activity, and therefore, makes side-chain motions indispensable to anyone interested in the motions of proteins. |
| Recently, there have been a number of high impact studies that highlight the role(s) that ps-ns methyl dynamics play in the free energy of binding via conformational entropy [11] as well as allosteric regulation of protein function [12]. As more systems that utilize these motions to regulate protein function are discovered, the biological relevance of ps-ns side-chain motions is becoming increasingly clear. Indeed, a recent study by Law et al. [13] suggests that side-chain dynamics may even be evolutionary conserved similarly to primary sequence. This review seeks to provide an overview of how side chain dynamics are measured and analyzed using NMR, as well as notable systems in which they play an important role in function. For more in-depth theoretical considerations regarding 15N (backbone) and 2H (side-chain) relaxation theory and analysis, readers are referred to reviews by Jarymowycz and Stone [14] and Igumenova et al. [9], respectively. |
| From Spin Relaxation to Protein Dynamics |
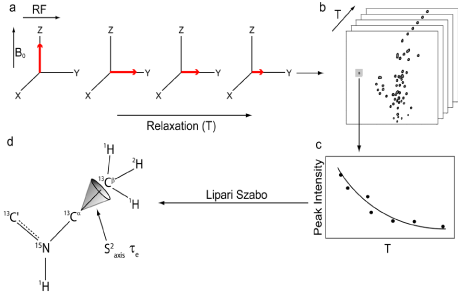
| Nuclear spin relaxation experiments allow protein dynamics on the ps-ns time regime to be measured by NMR. In these experiments, a series of radio frequency pulses are used to perturb nuclear spins away from their ground state (Figure 3a). Their “relaxation” back to equilibrium can be monitored as a function of time to obtain relaxation rates. There are two types of relaxation processes which excited nuclei are subject to: transverse relaxation and longitudinal relaxation. Transverse relaxation is the dephasing of coherent magnetization, as it precesses against a static magnetic field in the x-y plane. Longitudinal relaxation is the regeneration of the equilibrium Boltzmann population, by the return of bulk magnetization along the static magnetic field. Relaxation processes are not spontaneous; instead they are stimulated by local magnetic field fluctuations at or near the Larmor frequency of the target nucleus. Because the fluctuation of the local magnetic field is caused by molecular rotational motion, relaxation experiments can be utilized to yield information on the motions of bond vectors from spin relaxation measurements. |
| Measuring Spin Relaxation with NMR |
| For biomolecules, spin relaxation rates can be measured using a series of 2D heteronuclear single quantum coherence (HSQC) type experiments (Figure 3b), where each HSQC in the series utilizes a different relaxation time delay (T). During this relaxation time delay, molecular motions stimulate spin relaxation, which results in modulation of peak intensities. By plotting the change in peak intensity as a function of relaxation delay, relaxation rates can be obtained by fitting a single exponential to the observed decay (Figure 3c). In 1995, Muhandiram et al [15] published the original set of pulse sequences designed to measure the Dz (longitudinal) and Dy (transverse) relaxation rates of 2H nuclei. These pulse sequences are based on constant-time 1H-13C HSQC experiments and are fully detailed in Muhandiram et al [15]. Briefly, biomolecules are expressed in minimal media composed of ~60% D2O/~ 40% H2O, and supplemented with 15NH4Cl and 13C-glucose as the sole nitrogen and carbon sources, respectively. These conditions allow methyl groups to be composed of a mixture of isotopomers (i.e. 13CH2D and 13CHD2 where D is deuterium). Pulse sequences used to measure 2H relaxation rates select for signals that originate from the 13CH2D isotopomer, with the degree of 2H relaxation encoded in the intensity of 1H-13C HSQC resonances. The relaxation rates are then, in turn, used to fit the model free spectral density function to determine generalized order parameters specific for the methyl symmetry axis. |
| Since their original publication, there have been several modifications and improvements made to the original pulse sequences. In the original publication, a set of three experiments were necessary to obtain pure Dz or Dy relaxation rates. Briefly, the original pulse sequences measure triple spin coherences IzCzDz and IzCzDy, where I=1H, C=13C and D=2H). It is, therefore, necessary to run an addition experiment that measures IzCz relaxation to subtract its contribution to relaxation, thereby yielding pure Dz or Dy relaxation rates. However, Millet et al. [16] have updated the original pulse sequences to subtract this component within each Dz or Dy experiment itself, making it unnecessary to collect a third data set. The use of transverse relaxation optimized spectroscopy (TROSY, [17]), as well as experiments that measure 1H cross correlation relaxation [18], have also been developed to obtain order parameters for large molecules and protein complexes. These pulse sequences, along with new isotopic labeling schemes [19-21], are allowing the characterization of ps-ns methyl motions in proteins that were previously considered too large for NMR analysis. |
| There are multiple mechanisms by which motions on the ps-ns timescale can relax excited nuclear spins back to their ground state. Each mechanism’s total contribution to the overall relaxation process typically depends on the type of nucleus being analyzed, along with the strength of the static magnetic. Although there are many nuclei that are used for biomolecular NMR spectroscopy, this review will focus on the 2H nucleus, as it is typically used to measure sidechain dynamics. Nuclei with I>1/2, e.g. 2H, possess a nuclear electric quadrupole moment that interacts with local oscillations in the surrounding electric field gradients, thereby stimulating relaxation for excited spins. These interactions are highly effective at promoting relaxation, exceeding relaxation caused by other mechanisms by 1 to 2 orders of magnitude. Therefore, quadrupolar relaxation is the dominant relaxation mechanism for 2H spins, making relaxation rates easily fit and interpretable. The 2H nucleus has five independent operators with discrete relaxation rates that can linearly combined to describe the density matrix. The equations that describe these five independent relaxation modes are as follows [22]: |
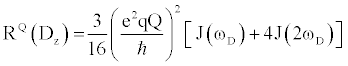 (1a) (1a) |
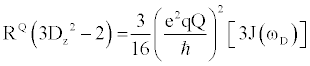 (1b) (1b) |
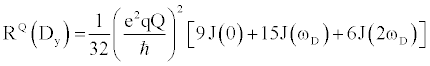 (1c) (1c) |
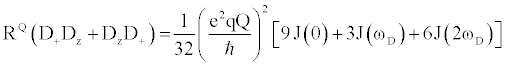 (1d) (1d) |
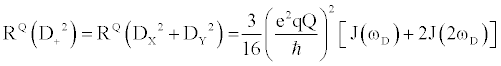 (1e) (1e) |
Where 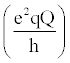 , the quadrupolar coupling constant, is approximately 167 kHz [23] and J(ω) is the value of the spectral density evaluated at the indicated frequency (0, ωD, 2ωD). Dy (in-phase transverse magnetization), D+Dz+DzD+ (antiphase transverse magnetization), and D+2 relaxation rates (double quantum magnetization) involve transitions between spin states, i.e. transverse relaxation, while Dz (longitudinal relaxation) and 3Dz2-2 relaxation rates (quadrupolar order) are related to the populations of spin states, i.e. longitudinal relaxation. These equations relate measured relaxation rates to the spectral density function, thereby providing a link between relaxation measurements and the frequency of molecular motions. It should be noted, however, that the measured relaxation rates report on the axially symmetric electric field gradient of the 2H nucleus, and not the 13C-2H bond vector of the side-chain methyl. , the quadrupolar coupling constant, is approximately 167 kHz [23] and J(ω) is the value of the spectral density evaluated at the indicated frequency (0, ωD, 2ωD). Dy (in-phase transverse magnetization), D+Dz+DzD+ (antiphase transverse magnetization), and D+2 relaxation rates (double quantum magnetization) involve transitions between spin states, i.e. transverse relaxation, while Dz (longitudinal relaxation) and 3Dz2-2 relaxation rates (quadrupolar order) are related to the populations of spin states, i.e. longitudinal relaxation. These equations relate measured relaxation rates to the spectral density function, thereby providing a link between relaxation measurements and the frequency of molecular motions. It should be noted, however, that the measured relaxation rates report on the axially symmetric electric field gradient of the 2H nucleus, and not the 13C-2H bond vector of the side-chain methyl. |
| Model-Free Spectral Density Analysis |
| The most general approach to describe the reorientational motions of a bond vector is to define a time-dependent rotational autocorrelation function. When assuming a motional model of isotropic molecular tumbling with no internal motion, the function can be defined as follows: |
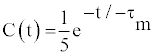 (2) (2) |
| This correlation function is particularly useful when separating motions that occur on a variety of time scales, and forms the basis for simple parametric models of angular bond vector motion [14,24]. The spectral density function, J(ω), can be obtained through the Fourier transformation of C(t), and can be expressed as |
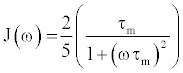 (3) (3) |
| The spectral density function describes the relative amplitude of bond vector motion at a given frequency. However, it assumes a motional model with isotropic tumbling and no internal motions, and therefore, cannot distinguish between molecular tumbling motions and internal protein dynamics. To separate the internal dynamics from the global motions, Lipari and Szabo [7,8] introduced a modified spectral density function that assumes no specific physical motional model. Known as the “model free” formalism, this modified spectral density function allows the isolation of internal motions from overall tumbling, by assuming that the internal dynamics of a protein are much faster than, and consequentially independent of, overall molecular tumbling. The model free spectral density function can be expressed as |
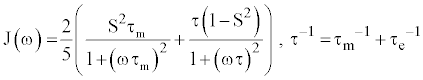 (4) (4) |
| Where S2 is the order parameter describing the degree of angular restriction for a given bond vector, τe represents the characteristic time of the bond vector motion, and τm is the rotational correlation time. For the majority of methyl groups, a single order parameter and correlation time is sufficient to describe local dynamics. However, a more detailed analysis of side-chain motions has been developed for residues that have additional, slower motions (i.e. low nanosecond), that are incompatible with the two-parameter model [16,25]. |
| As noted above, there are certain assumptions that need to be made, when using 2H relaxation measurements to obtain information on the motions of the C-CH3 symmetry axis of methyl side chains. These assumptions are necessary because the measure relaxation rates report on motions involving the principle axis of the electric field gradient tensor, not on the motions of the C-D bond vector that is of primary interest. Therefore, fitting 2H relaxation data to the model free formalism yields order parameters for the principle axis of the electric field gradient tensor. The two assumptions that allow measured 2H relaxation rates to be directly related to the biologically relevant motions of side chains are as follows: 1) The principle axis of the electric field gradient tensor is collinear with the C-D bond vector [23,26]. Because they are assumed to be collinear, the motions of the principle axis of the electric field gradient tensor are analogous to those of the C-D bond vector. 2.) The methyl group being analyzed has tetrahedral geometry. This condition allows the motions about the methyl symmetry axis to be separated from the motions of the symmetry axis itself. Although the rapid rotation about the axis is the primary motion of the C-D bond, it is not of primary interest for this review. By assuming that the methyl group has tetrahedral geometry, rotation about the axis can be removed from the S2 parameter by using Equation 2 where θ1 is the angle between the C-D bond and the averaging axis (109.5°) [15,23]. |
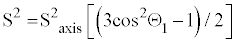 (5) (5) |
| S2axis therefore reports only on the motions of the methyl symmetry axis and not on motions about the methyl axis of rotation (Figure 3d). For τe, the characteristic time of motions about the methyl symmetry axis cannot be sufficiently separated from the characteristic time of motions of the symmetry axis; therefore, τe reports on a combination of both dynamic processes. Although it is presently unclear how to robustly interpret τe, it does provide a sensitive probe for monitoring changes in protein dynamics upon perturbations such as mutation or the binding of a target ligand [27,28]. |
| Functional Relevance |
| The functional relevance of side-chain motions on the ps-ns time regime have been well documented in a number of recent studies [29]. Atomic fluctuations, as measured by S2, were first realized to have potential functional relevance, when they were shown to be related to the Gibbs free energy equation [30]. An analytical relationship was then derived that linked order parameters measured by NMR to the local residual entropy of proteins [31,32]. While the relationship derived did not offer a reliable method for calculating absolute entropies from measured order parameters, it did provide a robust evaluation of relative entropic differences (e.g. differences between free and bound states). This relationship allowed the hypothesis that the relative differences in order parameters could serve as a proxy for changes in conformational entropy, provided the absence of correlated motions, or the extent of correlated motions is the same for both states. |
| Methyl Order Parameters as a Proxy for Conformational Entropy |
| The prediction that differences in order parameters could serve as a proxy for changes in the conformational entropy was verified experimentally by Frederick et al. [33], using calmodulin as a model system. The entropic contribution measured calometrically can be deconstructed into several components associated with the protein, the ligand, and the solvent as follows: |
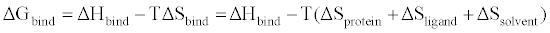 (6) (6) |
| where ΔGbind is the ΔG for a protein binding its target ligand. Both ΔSligand and ΔSsolvent are well established in the way they are able to affect the entropic contribution to biding free energy. What was less understood is the entropic contribution from the “structured” protein, which includes changes in its conformational, rotational, and translational entropy. Frederick et al. [33] selected calmodulin to further to examine the relationship between dynamics of side-chains and conformational entropy involved in binding. Calmodulin interacts and regulates a substantial number of proteins, allowing it to be an essential participant in calcium-mediated signal transduction pathways in eukaryotes [34,35]. Previous studies that monitored changes in fast side-chain motions upon ligand binding found a significant redistribution of these motions throughout the protein [36]. The question of whether this redistribution allows internal motions to “tune” affinity for different ligands, was a significant driving force for this study. Specifically, how conformational entropy is able to modulate the free energy of binding between a protein and its target ligand. To address this question, the dynamic response of calcium-saturated calmodulin (CaM) was monitored as a function of binding six peptides representing naturally occurring calmodulin binding partners. Backbone dynamics showed negligent variation across all complexes, indicating that they play no role in “tuning” binding affinity. However, the ps-ns motions of methyl-bearing side chains vary significantly with the type of target domain. The changes in methyl order parameters were then related to the conformation entropy, by using a simple harmonic oscillator model [31]. Despite potential limitations of this method [9,33], the total binding entropy to the six peptides correlated linearly (R2=0.78), with the corresponding apparent changes in conformational entropy, calculated by simple summation of the individual local entropies. This remarkable observation provided the first experimental evidence that order parameters measured by NMR could serve as a proxy for entropy associated with the binding free energy. |
| Entropic Modulation in a PDZ Domain |
| In addition, it has also been discovered that side chains can facilitate communication between sites that would not intuitively be suspected to be energetically linked based on their three dimensional structure alone [27,28,37-39]. Therefore, the ability of side changes to serve as a reservoir of conformational entropy, as well as to facilitate intramolecular communication, suggests that these motions may offer a foundation for allosteric communication without detectable conformational change.[40-43]. |
| PDZ domains are small monomeric proteins that are often found in scaffolding proteins that are composed of modular structures, that compose the larger multi-domained protein. The third PDZ domain from PSD-95/SAP90 (PDZ3), a neuronal scaffolding protein, is commonly thought of as the archetype of PDZ domains. The PDZ family has a highly conserved fold that consists of a 6-stranded half β-barrel and 2 α-helices [44]. However, there are many examples of members of the PDZ superfamily that contain additional structural elements or varying lengths of loops, β-strands, or helices [45-49]. Although considered the archetype of the PDZ superfamily, PDZ3 contains an atypical third α-helix on its carboxyl terminus. This additional structural element is thought to be biologically relevant because it has been shown to be phosphorylated, in vivo, at position Y397 [50]. To investigate the effects of this modification on protein structure and dynamics, Petit et al. [43] constructed a 7 amino acid deletion mutant of PDZ3, referred to here as Δ7ct. Δ7ct was designed to mimic the undocking of the C-terminal helical extension of PDZ3 upon phosphorylation of Y397 [51]. The thermodynamic properties of PDZ3 and Δ7ct binding to a naturally occurring target peptide, CRIPT [52], were assessed by isothermal titration calorimetry. These measurements indicated that the binding affinity of Δ7ct to CRIPT is reduced by 21-fold from PDZ3, and that, remarkably the difference between the two binding affinities are entirely due to the entropic component. As there was no evidence of gross structural changes that could explain this observed difference in binding affinity, relaxation experiments were employed to determine whether there were dynamic differences between the two constructs. Backbone dynamics revealed essentially no differences between the two constructs, and therefore, could not account for the observed variation in binding thermodynamics. A comparison of ps-ns side-chain motions of methyl containing residues, however, revealed global decreases in S2axis when compared to PDZ3. This global increase in flexibility is consistent with the increased entropic penalty paid upon CRIPT binding observed for Δ7ct. Indeed, the enhanced motions are quenched upon CRIPT binding with the Δ7ct bound complex, virtually mirroring the dynamic profile of the PDZ3 bound complex. It was, therefore, concluded that the additional entropic penalty observed for Δ7ct binding is due to increased motions (i.e. conformation entropy) in the side chains of the unbound protein. It is also worth noting that the dynamic changes occur throughout the protein, with a large number being distal to the binding pocket. These two points taken together, suggest that the changes in conformational entropy associated with side-chain dynamics, is the driving force behind the allosteric behavior observed in PDZ3. |
| Conformational Entropy, Not Structure, Modulates Binding in Catabolite Activator Protein |
| How the interplay between the three dimensional structure of a protein and its internal dynamics serve to regulate protein function is poorly understood. We often cannot rationalize the effect that perturbations of proteins via mutation, post-translational modification, or ligand binding have on proper function solely on the basis of structural information. To help better understand the relationship between structure, dynamics and function, Kalodimos et al. [53-56] have published several studies using catabolite activator protein (CAP) as a model system. CAP is a transcriptional activator that exists in solution as a homodimer, with a DNA binding domain at each monomers carboxyl terminus, and a ligand binding domain at each monomers amino terminus [57,58]. Briefly, two cyclic AMP (cAMP) molecules bind to the cAMP-binding domain of CAP, with negative cooperatively allosterically inducing a reorientation of its DNA-binding domain (DBD). It is this structural reorientation that switches CAP from an inactivated state, that is incapable of binding DNA to an active state that binds DNA with high efficiency. In the most recent study and the most pertinent to this review, Kalodimos et al. [53-56] use a series of allosteric mutants of CAP in the unliganded, cNMP-liganded (cAMP- and cGMP-liganded) and DNA liganded forms to dissect the contributions from structure and internal dynamics to binding energetics. It was first demonstrated by NMR chemical shift analysis that all of the CAP variants demonstrated a predictable linear derivation that connects resonances corresponding to the apo, inactivated form of CAP incapable of binding DNA and the activated cAMP bound form of CAP which readily binds DNA. Each CAP variant’s position relative to one another is indicative of the relative populations of inactive and active forms, with the average chemical shift resulting from the weighted fraction of the active and inactive populations [59-62]. Intuitively, the relative CAP binding affinity for DNA should correlate with the relative population of the active form of the protein. Namely, a CAP variant with a higher population of the active form of CAP should, in principle, have a higher binding affinity for DNA. Shockingly, this was found not to be the case with experimentally measured binding affinities showing no correlation with the relative population of the active form of CAP. This unexpected result demonstrated that the DNA binding affinity of CAP is modulated not primarily by structure, but instead by another, then unknown, factor. Isothermal titration calorimetry was used to thermodynamically characterize each variants energetic basis for binding DNA. The calorimetry data indicated that although the enthalpic contribution to binding free energy was remarkably consistent across all variants, the entropic contribution spanned a significant range of ~ 35 kcal mol-1. Because spatial fluctuations that bond vectors undergo had been shown to be related to conformational entropy [29-33,43,63-65], the changes in S2axis values of the side-chain methyl groups upon DNA binding were determined for each variant. Because the traditional 2H-based relaxation experiments [66] were too insensitive to obtain methyl order parameters for the large CAP-DNA complex (~ 90 kDa), 1H spin-based relaxation experiments that are optimally suited for large protein complexes were used [18]. To assess the contribution of protein motions to binding conformational entropy (-TΔSconf), changes in S2axis upon DNA binding were measured. These changes were then used to determine the conformational entropy of binding using the empirical calibration approach pioneered by Marlow et al. [63]. Remarkably, there was found to be a linear correlation between the total binding entropy, as measure by isothermal titration calorimetry and the conformational entropy, as determined by changes in S2axis. This led to the conclusion that conformational entropy determines whether protein-ligand interactions will occur, even in cases where the ligand binding interfaces are structurally identical. |
| Conclusion |
| The evidence for ps-ns side chain motions being an essential element involved in proper protein function is steadily increasing. The notion that proteins exists as static, single structures is steadily giving way to the realization that protein dynamically sample a myriad of substructures, within the native ensemble. The more that is learned about how these sampled states affect protein function, the more effective structure based drug design will become. By considering both the structural and the dynamical aspects of proteins, we will gain a more comprehensive understanding of protein functionality. |
| Acknowledgements |
| We thank Anthony B. Law and Paul J. Sapienza for their discussions and review of the manuscript. We gratefully acknowledge financial support from the Department of Biochemistry and Molecular Genetics at UAB. |
References
|
Figures at a glance
 |
 |
 |
| Figure 1 | Figure 2 | Figure 3 |
Post your comment
Relevant Topics
- Analytical Biochemistry
- Applied Biochemistry
- Carbohydrate Biochemistry
- Cellular Biochemistry
- Clinical_Biochemistry
- Comparative Biochemistry
- Environmental Biochemistry
- Forensic Biochemistry
- Lipid Biochemistry
- Medical_Biochemistry
- Metabolomics
- Nutritional Biochemistry
- Pesticide Biochemistry
- Process Biochemistry
- Protein_Biochemistry
- Single-Cell Biochemistry
- Soil_Biochemistry
Recommended Journals
- Biosensor Journals
- Cellular Biology Journal
- Journal of Biochemistry and Microbial Toxicology
- Journal of Biochemistry and Cell Biology
- Journal of Biological and Medical Sciences
- Journal of Cell Biology & Immunology
- Journal of Cellular and Molecular Pharmacology
- Journal of Chemical Biology & Therapeutics
- Journal of Phytochemicistry And Biochemistry
Article Tools
Article Usage
- Total views: 14304
- [From(publication date):
specialissue-2013 - Aug 29, 2025] - Breakdown by view type
- HTML page views : 9666
- PDF downloads : 4638
