Our Group organises 3000+ Global Conferenceseries Events every year across USA, Europe & Asia with support from 1000 more scientific Societies and Publishes 700+ Open Access Journals which contains over 50000 eminent personalities, reputed scientists as editorial board members.
Open Access Journals gaining more Readers and Citations
700 Journals and 15,000,000 Readers Each Journal is getting 25,000+ Readers
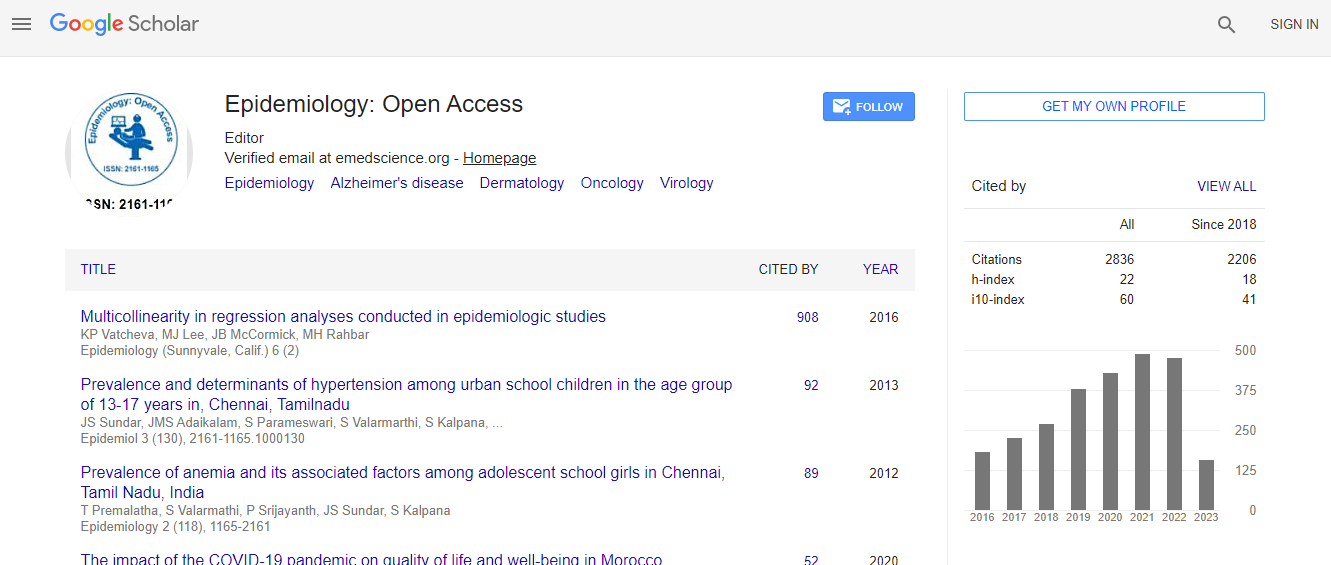
Google Scholar citation report
Citations : 3864
Epidemiology: Open Access received 3864 citations as per Google Scholar report
Epidemiology: Open Access peer review process verified at publons
Indexed In
- Index Copernicus
- Google Scholar
- Sherpa Romeo
- Genamics JournalSeek
- SafetyLit
- Access to Global Online Research in Agriculture (AGORA)
- Centre for Agriculture and Biosciences International (CABI)
- RefSeek
- Hamdard University
- EBSCO A-Z
- OCLC- WorldCat
- CABI full text
- Cab direct
- Publons
- Geneva Foundation for Medical Education and Research
- Euro Pub
- ICMJE
Useful Links
Recommended Journals
Related Subjects
Share This Page
Modeling and analyzing the dynamics of epidemic spreading on homogenous and heterogeneous networks
2nd International Conference on Epidemiology & Evolutionary Genetics
Lequan Min and Yao Hu
ScientificTracks Abstracts: Epidemiol

 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi